一道几何题的小思考

倪建

[摘  要] 解题能力是数学教师的一项必备的专业能力，但由于一些原因，很多教师却忽略了. 通过对一些有难度的习题的练习及阅读期刊，可以保持甚至提高教师的解题能力，有助于教师评定更高一级的职称.

[关键词] 几何题;解题能力;阅读

解题能力是数学教师的一项必备的专业能力. 对思维能力要求较高的问题进行探究思考，有助于教师解题能力和专业素养的提升. 教师的解题能力很重要，它直接影响了教师的解题教学，最终影响学生的数学学习. 最近同事参加高级职称笔试后问了笔者一道试题，有一定的难度，现对问题进行深入思考.

问题呈现

如图1，已知菱形ABCD的边长为a，P为对角线AC上的一个动点，∠BAD=30°，求PA+PB+PD的最小值.

问题解法探究

解法1：数形结合，建立坐标系，将几何问题转化为代数问题. 如图2，设OP=x，设f（x）=PA+PB+PD，则f（x）=acos15°-x+2，则f′（x）= -1+，令f′（x）=0，所以x=asin15°時，fmin（x）=acos15°+asin15°=2asin（15°+30°）=a.

分析：题目中的条件30°并不好用，所以想着简单一些，直接建立坐标系，将PA，PB，PD用未知量表示出来，转化为函数的最值问题. 此方法应用了一些高中的数学知识（求导，三角函数），虽然解决了问题，但总感觉“违规”，笔者想着肯定有更初等的方法.

解法2：利用菱形的轴对称性，得PB=PD，进而将问题转化为PA+2PB，即PA+PB. 联想将军饮马问题，利用30°这个特殊角和之间的关系可以给出下列解法. 如图3，作∠PAE=30°，PF⊥AE，则PF=PA，所以PA+PB=PF+PB. 当B，P，F三点共线时，（PF+PB）min=BG，因为∠BAE=45°，所以BG=AB=a. 所以PA+PB+PD=PA+2PB=2BG=a.

分析：利用菱形的轴对称性，将问题转化为λPA+PB，巧妙地应用了30°，解决了问题，有“运气”的成分. 笔者查阅了相关文章[1]，知道了这是个经典模型，关于直线的胡不归问题，关于圆的阿氏圆问题，最终都是转化为两点之间线段最短的问题. 文中还提到了费马点，三角形内部一点到三个顶点距离之和最小问题，可通过将某一个三角形旋转60°，将三条线段和最小的问题转化为两点之间线段最短的问题.

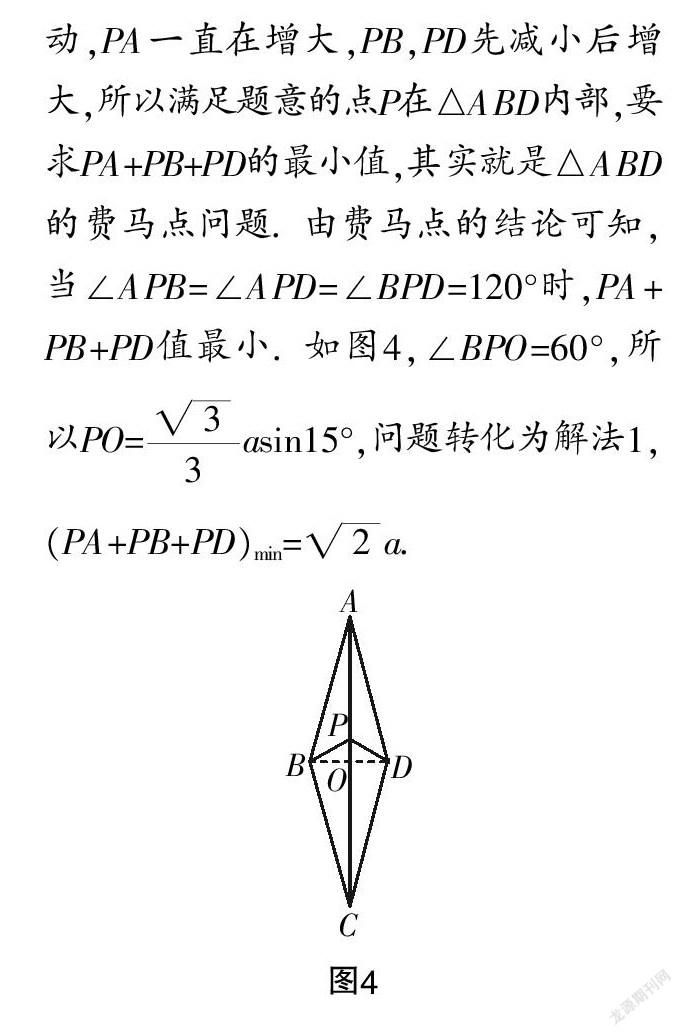
解法3：要想出现三角形，连接BD即可，随着点P在线段AC上自上而下运动，PA一直在增大，PB，PD先减小后增大，所以满足题意的点P在△ABD内部，要求PA+PB+PD的最小值，其实就是△ABD的费马点问题. 由费马点的结论可知，当∠APB=∠APD=∠BPD=120°时，PA+PB+PD值最小. 如图4，∠BPO=60°，所以PO=asin15°，问题转化为解法1，（PA+PB+PD）min=a.

感悟

1. 数学教师通常都很忙碌，如日常教学、批改作业、找学生订正作业，辅差. 同时还有很多数学教师当班主任，那就更忙了. 他们往往忽视了自己专业上的发展，很少去解难题、写文章、做课题. 他们是学校发展的主力军，在专业上停滞不前着实可惜. 这位同事最终没有评上高级职称，挺令人惋惜的，所以教师们要关注自己的专业发展，多解难题，如中考压轴题，以提高解题能力. 除了解题，还要研究解题教学，研究怎样讲授习题，使学生更容易理解.

2. 读专业的数学杂志有助于教师更快地提高专业素养，闭门造车断不可取. 笔者给出解法2属于灵光乍现，殊不知此类问题已有前人总结，即胡不归问题. 杂志上的文章都是精品，有优秀的数学同仁对教学经验的总结，也有极好的数学解题思想方法. 笔者也是因为查阅杂志才了解了胡不归问题、费马点问题，开卷有益. “要给学生一滴水，老师就需要有一碗水.”教师要多阅读、多反思，逐渐提升自身数学素养，并最终服务于日常教学，提升课堂教学的效果. 与此同时，教师也就减少了课下辅导学生的时间，用这些时间从事专业发展，形成良性循环.

参考文献：

[1] 周杨. 线段最值问题的难点突破[J].初中数学教与学，2020（19）：22-25.