Pythagorean模糊对称交叉熵及加权投影的多属性决策

韩二东，李占强

洛阳师范学院 商学院，河南 洛阳 471934

为打破直觉模糊集中专家对于方案在各属性下的隶属度和非隶属度的和不能超过1的约束，Yager等[1]推广了直觉模糊集，提出了能够描述隶属度和非隶属度之和超过1，而两者的平方和不超1的Pythagorean模糊集，从而更为精确地描述专家对各方案关于各属性的评价偏好，不仅比直觉模糊集表达的模糊现象范围更广、刻画和表达模糊信息的能力更强，而且提高了多属性决策应用的灵活性[2]。

自提出Pythagorean模糊集以来，基于Pythagorean模糊集以及各类型扩展形式的决策理论与方法受到学者们的广泛关注，相关研究主要分为3大类，首先是对其运算法则、得分函数、精确函数、信息测度等基础理论的研究，Zhang等[3]定义了Pythagorean模糊集的加法、乘法、数乘和幂运算，给出其得分函数与相互比较的基本方法，并提出了Pythagorean模糊集的相似测度；Gou等[4]研究了Pythagorean模糊集的连续性和可导性；刘卫锋等[5]考虑到隶属度和非隶属度之间可能存在的交叉影响，重新定义Pythagorean模糊数的运算法则，使得相关运算结果更为稳健，也更加符合常理；文献[6]针对基于代数积和代数和运算法则的局限性，定义了Pythagorean模糊Hamacher运算，并研究运算的相关性质；李德清等[7]研究了Pythagorean模糊集的距离测度；Garg[8]定义了Pythagorean模糊集的信息能量、相关指标及相关系数，并与已有的其他类型模糊集相关系数进行比较分析；刘卫锋等[9]受此启发，在定义Pythagorean犹豫模糊集的信息能量、相关指标的基础上，提出Pythagorean犹豫模糊集的相关系数及加权相关系数，从专家对不同方案评价的整体视角得到各方案的优劣次序，凸显Pythagorean犹豫模糊集表达决策者犹豫不决偏好信息的显著优势；此外，文献[10]定义了Pythagorean模糊集的熵和包含测度。

其次是Pythagorean模糊信息集成算子及其决策应用研究。Yager[11]提出了Pythagorean模糊加权平均算子（PFWA）和有序加权平均算子（PFOWG）；考虑到隶属度和非隶属度之间的关联和相互影响[5]，提出了Pythagorean模糊交叉影响加权平均算子（PFIWA）、交叉影响有序加权平均算子（PFIOWA）、交叉影响几何平均算子（PFIWG）及交叉影响有序加权几何平均算子（PFIOWG），并给出各算子的具体计算公式；针对属性间存在相互关联的多属性决策问题，彭定洪等[12]提出了Pythagorean模糊Heronian算子及加权算子，并讨论算子的性质；Garg[13]定义Pythagorean模糊Einstein运算下的一系列算子；考虑到Hamacher t-模和t-余模既是对代数积和代数和的推广，也是对Einstein积和Einstein和的推广，将Hamacher积和Hamacher和拓展到Pythagorean模糊环境[6]，定义了Pythagorean模糊Hamacher加权平均算子（PFHWA）、Hamacher有序加权平均算子（PFHOWA）、Hamacher加权几何算子（PFHWG）、Hamacher有序加权几何算子（PFHOWG）；常娟等[14]考虑各属性信息分布的疏密程度，提出Pythagorean密度集成算子；还涉及到Pythagorean模糊幂平均算子[15]、Pythagorean模糊幂Bonferroni集成算子[16]、Pythagorean模糊Choquet积分算子[17]、对称Pythagorean模糊加权平均算子[18]、Pythagorean模糊BM算子[19]、广义Pythagorean模糊算子等[20]算子，能够用于解决属性关联的多属性决策问题。此外，将Pythagorean模糊集与其他类型的模糊集结合，针对其拓展形式提出了一系列的信息集成算子，例如，Zhang[21]和Peng等[22]提出Pythagorean区间模糊集，并将QUALIFLEX方法应用于解决Pythagorean区间模糊多属性群决策问题；将Pythagorean模糊集由离散集合拓展到连续集合，杜玉琴等[23]探讨了基于Pythagorean三角模糊语言的Hamacher集成算子；范建平等[24]提出三角Pythagorean模糊集并研究了相关算子及性质；Khan等[25]将优先级平均算子（PA）与Pythagorean模糊集结合，提出了Pythagorean模糊优先级集结算子，随后翟运开等[26]定义犹豫Pythagorean模糊语言优先级集结算子，并由此构建解决属性间存在优先级关系的多属性决策方法；彭新东等[27]定义了Pythagorean模糊语言集和Pythagorean模糊软集，随后文献[28]在定义Pythagorean犹豫模糊语言集的基础上，提出相应的加权平均算子、加权几何算子及有序算子；李鹏等[29]基于Heronian算子提出Pythagorean模糊不确定语言加权Heronian平均算子（PFULWHM）和Pythagorean模糊不确定语言加权几何Heronian平均算子（PFULWGHM）。

第三是将传统多属性决策方法拓展到Pythagorean模糊环境，提出基于Pythagorean模糊评价的多属性决策方法。Zhang等[3]提出Pythagorean模糊TOPSIS法；Chen[30]构建Pythagorean模糊VIKOR法；Liang等[31]提出基于理想解的Pythagorean模糊三支决策方法；李美娟等[32]提出一种基于新得分函数和累积前景理论的Pythagorean模糊TOPSIS法；后续研究还涉及到Pythagorean模糊QUALIFLEX法[33]、基于信息熵的Pythagorean模糊LINMAP法[34]、带有可能度的区间Pythagorean模糊决策方法[35]、基于前景理论的Pythagorean模糊TODIM法[36]、基于前景理论和新距离测度的Pythagorean模糊决策方法[37]、基于前景理论的Pythagorean犹豫模糊不确定语言ELECTRE决策方法[38]、Pythagorean模糊投影法等[39]；李娜等[40]定义区间Pythagorean模糊数的相对熵并提出一种基于相对熵的AQM多属性决策方法，并考虑决策者的后悔规避和失望规避心理行为，基于构建的Pythagorean模糊熵提出风险型多属性决策方法。所提出的多种类型多属性决策方法已应用于投资决策、风险评估、医疗诊断、绿色供应商选择、人力资源选拔推荐等领域，取得了良好决策效果。

综上所述，当前关于Pythagorean模糊集决策理论与方法的研究取得了较为显著的研究成果。其中，关于算子理论及应用的研究，一类是在属性间相互独立、互不关联的假设前提下，提出基于Pythagorean模糊集的加权平均算子、加权几何算子、有序算子、广义算子或混合型算子，证明了各类算子的具体表达式，并详细讨论各算子的置换不变性、幂等性、单调性、有界性等性质，提出相应的多属性决策方法；另一类是针对属性间存在冗余、互补、偏好关系等关联性的多属性决策问题，将Choquet积分、Heronian平均算子、幂Bonferroni平均算子、Hamacher平均算子等扩展到Pythagorean模糊环境，提出了一系列信息集成算子及多属性决策方法，部分算子具有较强的一般性，通过讨论算子所含参数取值的变化对方案排序结果的影响进行灵敏度分析和对比分析，从而验证决策方法的有效性与可行性，参数取值变化体现出决策者的风险偏好或主观态度，此类算子具备良好的动态性和灵活性；但此类研究偏重于集成算子的定义、计算公式推导、性质、应用范围及特点分析，少部分算子的计算结果缺乏封闭性，所提出的决策方法往往假设决策者权重或属性权重完全已知，较少涉及如何确定决策权重的问题。其次，所提出的Pythagorean模糊多属性决策方法中使用到的距离测度往往是对直觉模糊集的欧式距离、Hamming距离等的平行推广，当对各备选方案与正理想解、负理想解或其他参考点进行偏差度量时，容易造成逆序情形的发生，即通过计算各备选方案与正理想解的距离测度所得排序结果，同各备选方案与负理想解的距离测度所得排序结果并不一致，甚至两种优劣次序存在较为明显的差异。再次，模糊熵尚未充分扩展到Pythagorean模糊多属性决策方法中，已有研究通过定义Pythagorean模糊熵确定属性权重，亦或是根据各方案与正、负理想方案的相对熵，构建所有方案满意度最大化的规划模型确定属性权重，但基于Pythagorean模糊熵的偏差度量仍然会产生逆序问题，也在一定程度上造成决策信息的损失。

鉴于以上分析，本文通过定义Pythagorean模糊对称交叉熵取代欧式距离等距离测度来度量各方案与正、负理想方案的偏差，有效规避两种方案排序结果不一致的不合理现象，将Pythagorean模糊数之间的对称交叉熵纳入灰色关联贡献度的计算，以确定各属性权重；通过各备选方案到正、负理想方案的标准化加权投影，由双向投影构造贴近度获取各方案优劣次序，从而提出一种基于Pythagorean模糊对称交叉熵及标准化加权投影的多属性决策方法。

1 基本概念

（1）若s(α1)＞s(α2)，则α1＞α2；

（2）若s(α1)＜s(α2)，则α1＜α2；

（3）若s(α1)=s(α2)，则 比 较π1和π2的 大 小，当π1＞π2，则α1＜α2；当π1＜π2，则α1＞α2。

该得分函数兼顾决策参与者的从众心理，同时将隶属度、非隶属度和犹豫度纳入Pythagorean模糊数之间大小的比较，无需通过精确函数进行二次比较，避免出现与直觉相悖的比较结果，具有较强的区分能力。

2 Pythagorean模糊对称交叉熵

根据Pythagorean模糊集A、B的定义，易知H(A,B)≥0，H(A,B)=0当且仅当A=B；但很显然，A到B的Pythagorean模糊交叉熵并不满足对称性，即H(A,B)一般不等于H(B,A)，因此，H(A,B)虽可作为两个Pythagorean模糊集A、B之间差异程度的度量，但H(A,B)并不是两个Pythagorean模糊集之间真正的距离。在定义4的基础上，同理可定义如下Pythagorean模糊集B到A的模糊交叉熵：

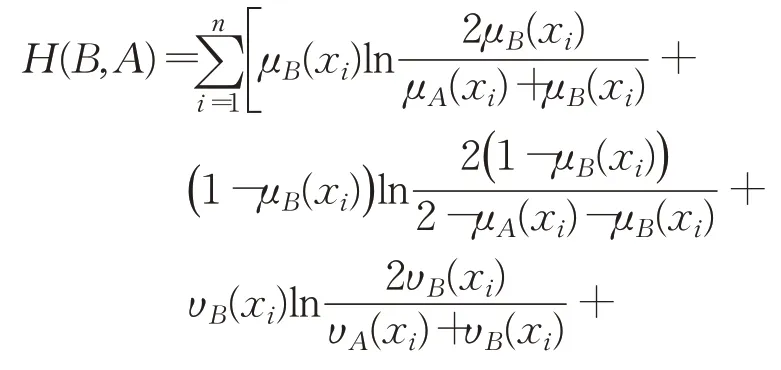
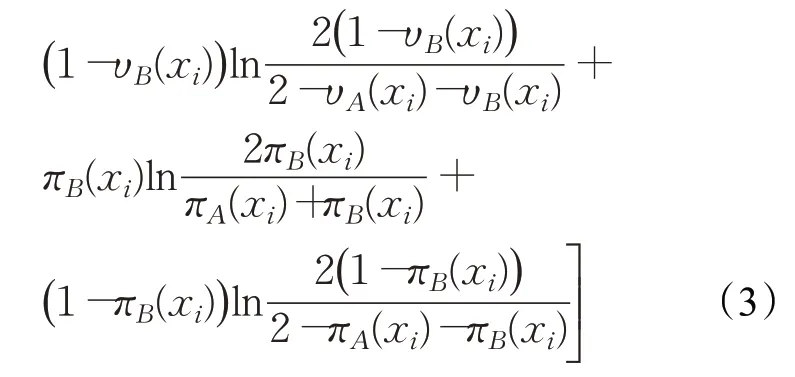
从而得到如下包含H(A,B)和H(B,A)且满足对称性的Pythagorean模糊对称交叉熵：

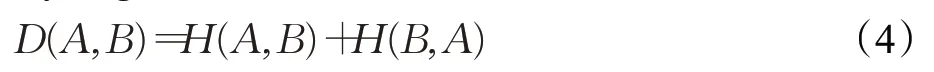
定理1Pythagorean模糊集A与B的对称交叉熵D(A,B)满足如下性质：

（1）D(A,B)≥0，D(A,B)=0当且仅当A=B；

（2）D(A,B)=D(B,A)；

（3）D(A,B)≤6n。

证明首先，根据Pythagorean模糊对称交叉熵的定义，显然D(A,B)≥0；若已知D(A,B)=0，则必有H(A,B)=0且H(B,A)=0，从而可得A=B；反过来，若A=B，则有H(A,B)=H(B,A)=0，那么D(A,B)=0。其次，根据式（2）～式（4），显然有D(A,B)=D(B,A)成立，从而（1），（2）得证。下面证明（3），由于：

同理，可得H(B,A)≤3n，因此可得D(A,B)≤6n，从而（3）得证。

由Pythagorean模糊集A与B的对称交叉熵D(A,B)的定义及性质，可知D(A,B)不仅是A与B之间偏差程度的度量，且满足对称性和有界性，能够避免出现A或B→{ 0,1),…,(0,1)}（或{(1,0),…,(1,0)}）时交叉熵的值趋向于无穷大的情况。

定理2Pythagorean模糊集A与B的加权对称交叉熵Dω(A,B)满足如下性质：

（1）Dω(A,B)≥0，Dω(A,B)=0当且仅当A=B；

（2）Dω(A,B)=Dω(B,A)；

（3）Dω(A,B)≤6。

证明其中（1）、（2）与定理1类似，显然成立。对性质（3），有：

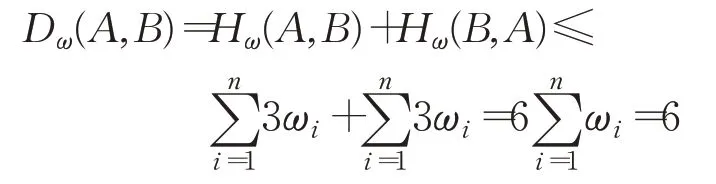
即（3）成立。

3 基于Pythagorean模糊对称交叉熵及标准化加权投影的多属性决策方法

3.1 基于Pythagorean模糊对称交叉熵及灰关联确定属性权重

针对决策专家给出的Pythagorean模糊决策矩阵M，设效益型属性集为I1，成本型属性集为I2，且C=I1⋃I2，对各属性评价信息进行规范化处理，可得：

在PF-TOPSIS法、PF-VIKOR法或其他衡量备选方案差异的多属性决策方法中，往往采用欧氏距离作为距离测度度量不同方案与理想解的差异程度，容易出现与正理想解距离更近的方案同时与负理想解的距离也更近，也即通过备选方案与正理想解、负理想解的距离测度所得两种方案排序结果存在差异，导致排序结果并不能真实反映各备选方案的优劣程度。与此相反，由于方案Ai与正理想方案A+、负理想方案A-的Pythagorean模糊对称交叉熵满足对称性、有界性及三角不等式，排除备选方案Ai本身是正理想方案或负理想方案的特殊情况，通过各方案与正理想方案A+的Pythagorean模糊对称交叉熵所得方案优劣次序，和各方案与负理想方案A-的Pythagorean模糊对称交叉熵所得方案优劣次序保持一致，能够避免出现逆排序的决策结果。因此，将Pythagorean模糊对称交叉熵替换欧式距离等作为两个或多个Pythagorean模糊集（数）距离测度的度量具有显著优势。以下将Pythagorean模糊对称交叉熵纳入灰色关联贡献度分析，并以此确定各属性权重。

在式（7）基础上，定义方案Ai与正理想方案A+关于单个属性Cj的Pythagorean模糊对称交叉熵为：

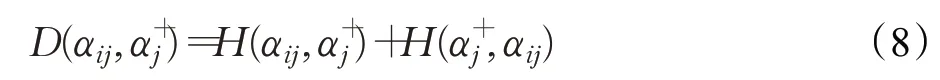
计算方案Ai与正理想方案A+关于属性Cj的灰色关联系数为：

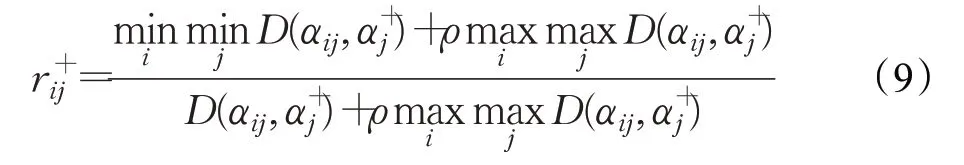
其中，ρ∈[0,1]为分辨系数，通常取值为0.5，其作用在于提高方案Ai与正理想方案A+关于不同属性评价所得关联系数之间的差异显著性。

可得属性Cj的灰靶贡献度为：

单个属性的灰靶贡献度越大，则该属性对方案排序的贡献越大，对方案评价结果的重要程度越大。因此，可依据各属性的灰靶贡献度来衡量各属性的权重大小，灰靶贡献度越大的属性，其权重也越大，从而得到属性Cj的权重为：

3.2 基于标准化加权投影的Pythagorean模糊排序方法

则备选方案Ai在正理想方案A+上的投影可定义为：

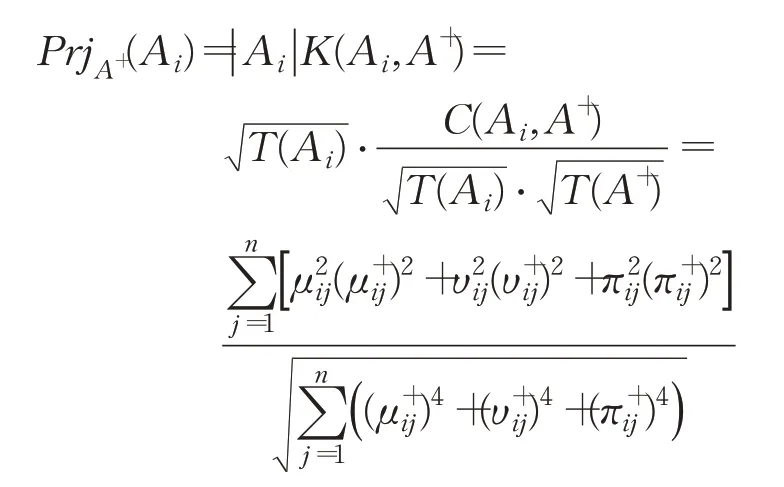
其中，K(Ai,A+)表示备选方案Ai与正理想方案A+的相关系数。

更进一步，考虑到多属性决策问题中各属性权重的差异，从而定义备选方案Ai在正理想方案A+上的加权投影为：

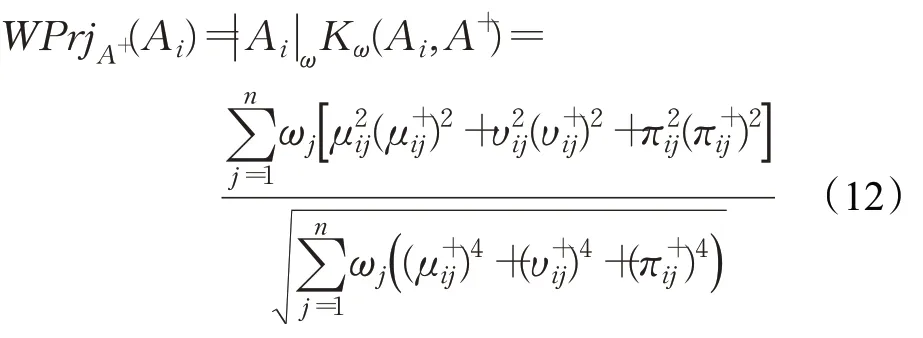
其中，|Ai|ω表示备选方案Ai作为Pythagorean模糊集的加权模，K(Ai,A+)表示备选方案Ai与正理想方案A+的加权相关系数，具体表达式如下：

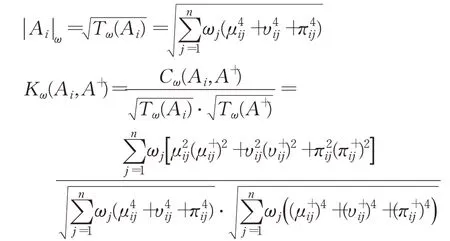
由投影理论在模糊多属性决策中的应用，可知投影值计算结果可能会出现WPrjA+(A+)＜WPrjA+(Ai)，而从直觉和实际出发，正理想方案A+到自身的投影值应该更大，显然该结果是不合理的。因此，将式（12）标准化处理，提出如下备选方案Ai在正理想方案A+上的标准化加权投影。

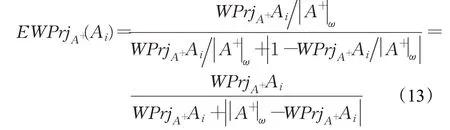
同理，备选方案Ai在负理想方案A-上的标准化加权投影定义为：

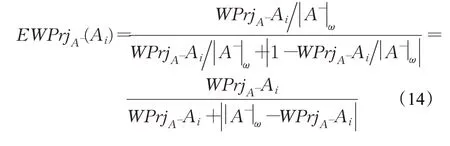
根据以上Pythagorean模糊加权投影和标准化加权投影的定义，可知E WPrjA+(Ai)越大，方案Ai与正理想方案A+越接近；EWPrjA+(Ai)越小，方案Ai与正理想方案A+越远离。同时，EWPrjA-(Ai)越大，方案与负理想方案A-越接近；EWPrjA-(Ai)越小，方案Ai与负理想方案A-越远离。由此，定义贴近度为：

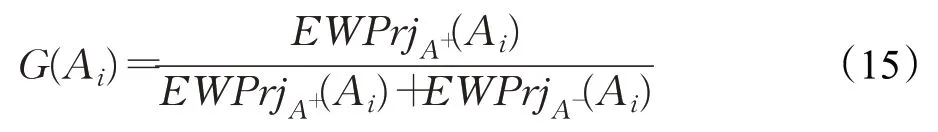
贴近度G(Ai)越大，方案Ai越优，从而得到各备选方案的优劣次序。

3.3 决策步骤

步骤1针对决策者以Pythagorean模糊数对各备选方案关于各属性开展评价的多属性决策问题，由式（5）对Pythagorean模糊决策矩阵M进行标准化处理，针对规范化的Pythagorean模糊决策矩阵，由式（1）计算方案Ai(i=1,2,…,m)在属性Cj(j=1,2,…,n)下Pythagorean模糊值的得分函数，从而由式（6）确定正理想方案A+和负理想方案A-。

步骤2由式（2）～式（4）及式（7）、式（8）计算方案Ai与正理想方案A+的对称交叉熵，进而由式（9）得到方案Ai与正理想方案A+关于属性Cj的灰色关联系数。

步骤3根据式（10）计算属性Cj的灰靶贡献度，进一步由式（11）对灰靶贡献度归一化处理，并确定各属性权重。

步骤4由求得的各属性权重，通过式（12）计算各备选方案在正理想方案上的加权投影值WPrjA+(Ai)，并由式（13）得到标准化加权投影值EWPrjA+(Ai)；进一步，由式（14）计算各备选方案在负理想方案上的标准化加权投影值EWPr jA-(Ai)。

步骤5通过式（15）计算各备选方案的贴近度G(Ai)，并依据贴近度大小对方案排序择优。

4 实例分析

自我国进入新发展阶段，亟需落实新发展理念、构建新发展格局，这就要求新时代的经济特区要坚定不移实施创新驱动发展战略，抓住粤港澳大湾区建设重大历史机遇积极作为，在经济特区发展中作出新贡献。假设经济特区内某政府、高校、科研院所和大型企业，联合开展规划设计并谋求合作，从而促进区域经济高质量发展，其中较为重要的实施途径是开展一系列的R&D项目。现假设有6个R&D项目可供选择，记为Ai(i=1,2,…,6)，决策专家拟从技术水平C1、公司和战略规划C2、监管机构设置状况C3、市场发展水平及趋势C4、财务状况C5、项目应用前景C6这6个指标展开评估，拟以Pythagorean模糊数给出各备选R&D项目在所有指标下的评价信息，具体如表1所示。

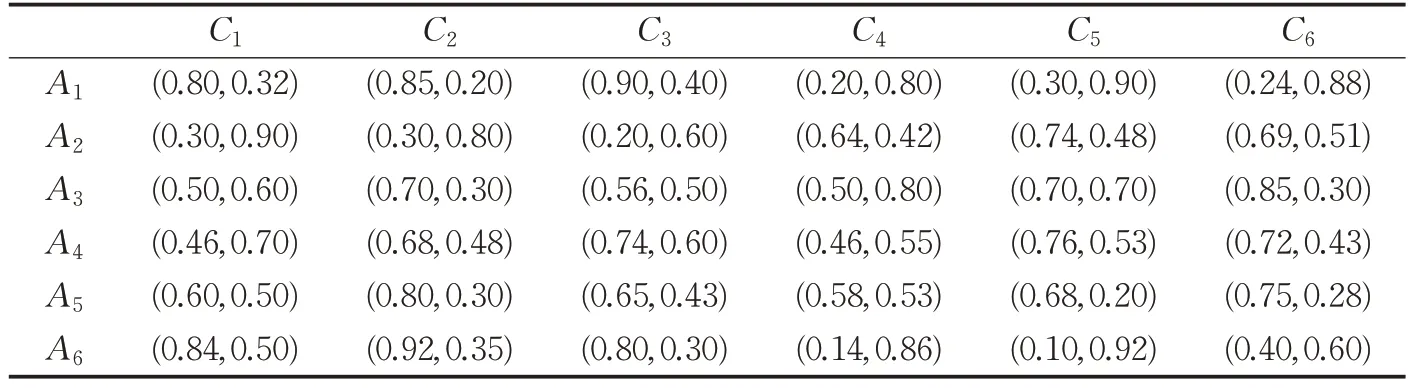
表1 专家提供的Pythagorean模糊评价信息Table 1 Pythagorean fuzzy evaluation information provided by expert

4.1 决策步骤

步骤1由于各属性均为效益型属性，无需进行规范化处理，直接由式（1）计算所有Pythagorean模糊评价值的得分函数，并由式（6）得到该决策矩阵的正理想方案A+和负理想方案A-分别为：

步骤2为将Pythagorean模糊交叉熵与灰关联分析相结合确定各属性权重，由式（2）计算方案Ai到正理想方案A+的关于属性Cj的交叉熵H(αij,α+j)，其构成的交叉熵矩阵记为H1；同时由式（3）计算正理想方案A+到方案Ai关于属性Cj的交叉熵H(α+j,αij)，其构成的交叉熵矩阵记为H2，从而可得：

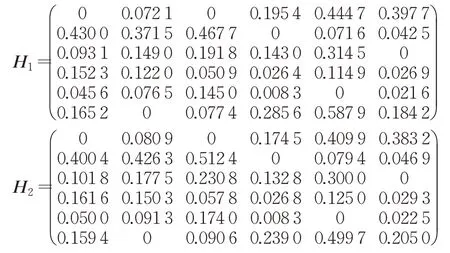
由式（4）、式（7）及式（8）计算方案Ai与正理想方案A+关于属性Cj对称交叉熵D(αij,α+j)，其构成的交叉熵矩阵D为：

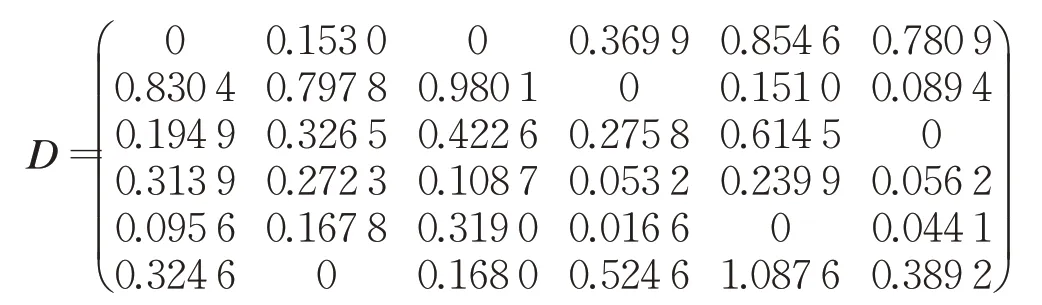
进一步，由式（9）得到各方案与正理想方案A+关于属性Cj的灰色关联系数r+ij(i=1,2,…,m;j=1,2,…,n)，其构成的矩阵R+为：

4.2 比较分析

首先，在上述决策步骤4分别计算各备选方案在正理想方案和负理想方案上的加权投影时，使用到各备选方案与正理想方案、负理想方案的加权相关系数，其计算结果分别为：

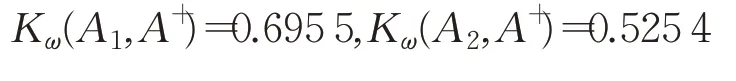
备选方案与正理想方案的加权相关系数越大，方案越优，所得方案排序结果为A5≻A4≻A3≻A1≻A6≻A2；相反，备选方案与负理想方案的加权相关系数越小，方案排序越靠前，所得方案排序结果为A5≻A4≻A6≻A1≻A3≻A2。两种方案排序结果中，前者与本文决策方法在所得结果在A1、A6的排序上存在差异；后者与本文所得结果在A1、A3、A6的排序上存在差异，但最优方案始终是A5且最劣方案始终为A2，验证了本文决策方法的有效性与合理性。

其次，将文献[3]提出的PF-TOPSIS法、文献[31]提出的基于理想解的Pythagorean模糊三支决策方法以及文献[32]提出的基于新得分函数和累积前景理论的TOPSIS法用于解决本文算例，由各备选方案的贴近度获取的方案排序结果如表2所示。

表2 不同决策方法下各备选方案的贴近度及排序结果Table 2 Closeness degree and ranking results of all alternatives under different decision-making methods

由上述对比分析结果可知，本文决策方法所得排序结果与文献[31]、文献[32]完全一致，与文献[3]只在方案A1、A6的先后次序上存在差异，其余方案优劣次序也保持一致，相比于这3种决策方法，本文方法在度量各方案与正理想解或负理想解的距离时，采用Pythagorean模糊交叉熵代替欧式距离等距离测度，使得依据所有备选方案与正理想解、负理想解的Pythagorean模糊交叉熵所得两种排序结果保持一致，不会造成某些方案逆排序现象的发生，决策结果更加科学合理。

再次，将本文决策方法与基于Pythagorean模糊集成算子的多属性决策方法进行对比分析，主要涉及到PFIWA算子[5]、PFHWG算子[6](γ=0.5)、PFHWA算子[6](γ=0.5)、PFEWG算子[13]、PFWG算子[20]，具体比较情况如表3所示。

由表3可知，5种类型算子所得方案排序结果与本文决策方法所得排序结果虽在部分方案的优劣次序上存在差异，但最优方案始终是A5，再次验证了本文决策方法的有效性。方案具体排序存在差异，主要是由于本文决策方法与基于不同类型Pythagorean模糊集成算子的多属性决策方法的决策机制不同；本文方法采用Pythagorean模糊交叉熵取代欧氏距离等距离测度度量各方案与正、负理想解之间的距离，能够使得与正理想解距离更近的备选方案一定与负理想解的距离更远，避免产生逆序问题，进而基于灰色关联贡献度确定各属性权重，计算各方案与正、负理想方案的标准化加权投影，通过构造贴近度得到最终决策结果。而基于算子理论的决策方法是通过不同类型的Pythagorean模糊集成算子得到各方案的综合属性值（仍以Pythagorean模糊数表示），依据得分函数对各方案排序择优；例如，PFIWA算子考虑到Pythagorean模糊数中隶属度和非隶属度之间可能存在的交叉影响；PFHWG算子和PFHWA算子以Pythagorean模糊Hamacher运算为基础构造，是一类范围更广的t-模和t-余模，是对PFEWG算子和PFWG算子的推广，更具有一般性；各类算子所包含参数的取值变化体现出决策者主观判断或对决策对象风险态度的变化趋势。相比之下，本文决策方法对方案优劣关系的判断更为精细，所得方案优劣次序更为稳定，符合实际决策情境。

表3 不同集成算子下各备选方案的综合属性值及排序结果Table 3 Comprehensive attribute values and ranking results of each alternative under different integration operators

5 结束语

考虑到传统欧式距离等距离测度的不足之处，与正理想解的距离更近的备选方案可能与负理想解的距离也更近，即通过各方案与正理想解的偏差大小所得优劣次序和各方案与负理想解的偏差大小所得优劣次序并不一致，导致排序结果并不能真实反映多个备选方案的优劣关系。本文以各备选方案与正理想方案的Pythagorean模糊对称交叉熵，作为各方案与正理想方案在单个属性下的评价偏差，通过灰色关联分析中的属性贡献度大小确定各属性权重；计算各备选方案到正、负理想方案上的加权投影值，将所得两类加权投影值进行标准化，通过各备选方案与正、负理想方案的标准化加权投影值构造贴近度，最终实现对各方案的排序择优。下一步，可将Pythagorean模糊对称交叉熵和加权对称交叉熵扩展到Pythagorean犹豫模糊集、Pythagorean模糊不确定语言变量等决策环境下，并针对未知的决策者权重或属性权重，基于Pythagorean模糊对称交叉熵构建多属性决策模型，解决相应的多属性决策问题。