Synchronization in multilayer networks through different coupling mechanisms
Xiang Ling(凌翔) Bo Hua(华博) Ning Guo(郭宁) Kong-Jin Zhu(朱孔金)Jia-Jia Chen(陈佳佳) Chao-Yun Wu(吴超云) and Qing-Yi Hao(郝庆一)
1School of Automotive and Transportation Engineering,Hefei University of Technology,Hefei 230009,China
2School of Mathematics and Computational Science,Anqing Normal University,Anqing 246133,China
Keywords: coupling mechanisms,synchronization phenomena,coupled networks
1. Introduction
Synchronization is a collective dynamic phenomenon in which the rhythms of multiple oscillating units adjust and adapt to each other under weak coupling; it has been intensively investigated over the past 40 years.[1]Since the discovery of the small-world characteristics (by Watts and Strogatz[2]) and scale-free characteristics (by Barab´asi and Albert[3])of complex networks,researchers began to combine the dynamic properties of nodes with the complex structure of networks to study the synchronization behavior of complex networks. The basic mechanism behind many cooperative actions derives directly from synchronization in complex and nonlinear systems. The synchronization of complex networks has become an important area of research in network science.
In this paper we investigate the phenomenon of transition to synchronization in two-layer coupled networks. Synchronization in complex systems is characterized by the transition from an incoherent state to a synchronized state with an increase in coupling strength, andvice versa. In particular, explosive synchronization (ES),i.e., an abrupt irreversible and discontinuous synchronous transition with a hysteresis loop,can occur.
Although many studies have focused on the synchronization of complex networks, the research is still not thorough and needs to be continued.[4-11]The common mathematical models of complex dynamic network synchronization include the coupled differential equation model and the Kuramoto oscillator model, which mainly describe the complete synchronization and phase synchronization of network nodes. There are three main research methods for investigating complex dynamic networks: global synchronization stability analysis using the Lyapunov function method,[12,13]the local synchronization main stability function method[14,15]and the global synchronization connection graph stability method of timevarying networks.[16]With the development of complex networks,the Kuramoto model has become one of the most popular synchronization models using coupled dynamic systems for synchronization research.
Recently,the majority of the studies have looked at coherent behavior within a single network, where each node in the network reaches the same steady state. This kind of synchronization within a network is called inner synchronization.[17]It ignores a very important factor that the components of a complex system may interact simultaneously through two or more dynamics, and these dynamics depend on each other in specific ways. There also exist other kinds of network synchronization to describe interconnected networks, such as outer synchronization between two or more networks.[18,19]In 2010 Muchaet al.[20]proposed a new type of network,a multiplex network,which can also be synchronized.Xuet al.[21]investigated the synchronizability of two-layer networks. Nicosiaet al.[22]introduced a framework to intertwine the dynamical processes of a multilayer network, which can induce spontaneous ES. In particular, there is growing interest in studying the phenomenon of ES in multilayer networks since Zhanget al.[23]extended ES to adaptive and multilayer networks; this includes intralayer synchronization,[24]synchronization in frequency displaced,[25]synchronization enhanced by delay[26]and ES induced by inhibition.[27]Multilayer networks can better describe the reality of interconnected networks than singlelayer networks with the connection of their links showing rich synchronization phenomena. However,there are massive nodes of a complex network in the real world. It would be costly and impractical to control all nodes to manipulate the dynamics of the network. Therefore, we choose two independent scale-free networks and propose the coupled network mechanism according to three specific coupling mechanisms which show a unique synchronization phenomenon. It is more feasible to control some nodes of the network. We then investigate whether the coupled networks are affected under different frequency distributions. Finally, we verify the robustness of the scheme by considering different network topologies in coupled networks.
The paper is organized as follows. In Section 2 we describe the network model with three different coupling mechanisms and the adaptive Kuramoto model in a multilayer network in detail. In Section 3 we discuss the simulation results.In Section 4 we summarize our work and discuss it.
2. The model
2.1. Network model and coupling mechanisms
A scale-free network is generally considered to be the backbone of many complex systems and encompasses two important general concepts: growth and preferential attachment[28,29]Without loss of generality, we consider the coupled networks in this paper as two interconnected networks(I and II); these are generated by the Barab´asi-Albert (BA)network model to capture the essence of many network systems in the real world. Layers I and II have the same network size(i.e.the same number of nodesNI=NII=Nand the same average degree〈kI〉=〈kII〉=〈k〉). These two interconnected networks are connected by adding links that provide paths for the synchronization process between them. Here, we assume that the interconnection is one-to-one. This means that a node in layer I can have at most one link connecting it to a node in layer II.We use the coupling probabilityPdefined by

whereNisandNare the number of interconnected nodes and the network size, respectively. It is obvious that 0≤P ≤1.WhenP=1, all nodes in layer I have interconnected neighbors in layer II.WhenP=0.5,the nodes in layer I have half of the neighbors connected in layer II.WhenP=0, the coupling system is simplified to two independent networks.
In two-layer networks,apart from the density of the interconnected nodes,the connection mode of these nodes also has a significant impact on the dynamics of the coupled networks.Previous studies have shown that coupling mechanisms affect traffic network dynamics.[30-32]Nodes between two-layer networks are coupled in the order of degree. This reflects different coupling mechanisms. What we are interested in here is the rich synchronization dynamics that arise from these different mechanisms of coupling in network systems. We first sort the nodes into networks I and II in descending order of degree. Then the nodes are coupled one by one until the coupling probabilityPis reached. The three coupling methods studied in this paper are as follows:
(i)Assortative coupling: the node with the largest degree of network I is connected with the node with the largest degree of network II,the node with the second largest degree of network I is connected with the node with the second largest degree of network II,and so on.
(ii)Disassortative coupling: the node with largest degree of network I is connected with the node with the smallest degree of network II,the node with the second largest degree of network I is connected with the node with the second smallest degree of network II,and so on.
(iii)Anti-assortative coupling: the nodes of two networks are connected following ascending order of degree. The node with the smallest degree of network I is connected with the node with smallest degree of network II,the node with the second smallest degree of network I is connected with the node with the second smallest degree of network II,and so on.
2.2. Adaptive Kuramoto model in multilayer network
The synchronization behavior of oscillators can be studied mathematically,[33]and a large amount of work has been carried out on this subject.[34-37]Kuramoto proposed that the synchronization of a coupled system with a finite number of oscillators can be described by a simple phase equation.[38,39]In recent years the Kuramoto model has become one of the most popular models for studying the synchronization dynamics of complex networks.[40]
According to the above network model and coupling mechanism, we select nodes from two layers with a certain coupling probabilityP, then they are coupled to each other by forming dependency links. For convenience, the coupled node pairs have the same indexi. In the absence of interlayer interaction, the dynamics of two layers are governed by the adaptive Kuramoto model.θi,1andθi,2denote the phases of thei-th oscillator(i=1,...,Nis)in layers I and II,respectively(the dot represents the temporal derivative and subscripts 1 and 2 stand for layers I and II).Here,their evolutions are governed by the following differential equations:
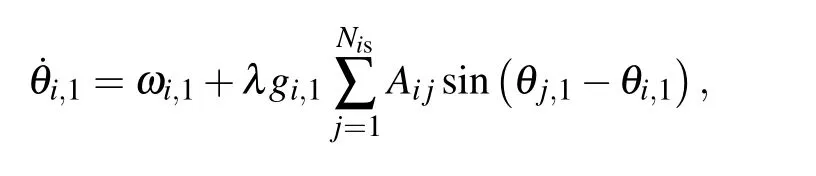

whereki,1andki,2denote the degree of thei-th node of the layers I and II,respectively,andφ1andφ2are the average phase of the ensemble of all neighbors of thei-th node of layers I and II.
To measure the synchronization level in the two-layer networks we use the order parametersR1andR2(global order parameters)

where 0≤R1,R2≤1, whileψ1andψ2denote the average phases of layers I and II,respectively,of all phases in this system.
3. Simulation results
To investigate the synchronization phenomena of twolayer networks with the three specific coupling mechanisms we perform extensive numerical simulations of Eq. (2) using the fourth-order Runge-Kutta algorithm with time stepδh=0.01. We perform forward (backward) numerical continuation as the coupling strengthλincreases (decreases) by increments (decrements) ofδλ=0.01. Then the stationary values of the global order parametersR1andR2for eachλare calculated. Each numerical simulation needs sufficient time(2×105time steps). After the steady state of a certain coupling strength has been calculated,this calculated steady state is taken as the initial state of the new coupling strength calculated in the next iteration.
For the proposed investigation, we consider two heterogeneous Barab´asi-Albert (BA) networks with the same network sizeNI=NII=1000 and the same average degree〈kI〉=〈kII〉=12,which are coupled through the three different coupling mechanisms with specific coupling probabilityPmentioned above,namely assortative coupling,disassortative coupling and anti-assortative coupling. The initial phase and natural frequency of the Kuramoto oscillator are uniformly distributed randomly in the interval[-π,π].
Figure 1 shows the dependence of the global order parametersR1andR2in two-layer networks on the coupling strengthλduring forward and backward continuation. The coupled networks consist of two different BA networks with four coupling probabilities,p(0.1, 0.4, 0.8, 1), for three different coupling mechanisms. The upper and lower rows represent layers I and II of the network, respectively. The left,center and right columns represent assortative coupling,disassortative coupling and anti-assortative coupling, respectively.It can be seen from Fig.1 that the synchronization phenomena in the two-layer networks are different under different coupling mechanisms, but the phenomena are basically the same at layers I and II.Under the assortative coupling mechanism,ES occurs in both layers of the network with the increase of coupling strength(see Figs.1(a)and 1(d)). The critical points of forward and backward transitions in ES increase with the increase in coupling probabilityp. Moreover,we observe that the area of the hysteretic zone increases with the increase ofp, indicating thatphas an enhancement effect on ES. Under the disassortative coupling mechanism,a smooth synchronous transition occurs in both layers of the network with the increase in coupling strength (see Figs. 1(b) and 1(e)). With the increase in coupling probabilityp,the transition of nodes in the network to synchronization requires a larger coupling strength. It can be inferred that the small synchronous clusters in the network are suppressed in both layers I and II under the disassortative coupling mechanism. Under the anti-assortative coupling mechanism,the smooth synchronous transition phenomenon also occurs in both layers of the network with increase in the coupling strength(see Figs.1(c)and 1(f)). However, ES occurs when coupling probabilitypis equal to 1 in both layers of the network because the structure of the twolayer networks in anti-assortative coupling is the same as the structure of the two-layer networks in assortative coupling.

whereT ≫1. Figure 2 shows the evolution of the global order parametersR1andR2in layers I and II, the effective

Fig. 1. Dependence of global order parameters R1 and R2 on λ for three different coupling mechanisms during forward and backward continuations. Panels(a)-(c)represent assortative coupling,disassortative coupling,and anti-assortative coupling of layer I,respectively,and panels(d)-(f)represent assortative coupling,disassortative coupling,and anti-assortative coupling of layer II,respectively. Synchronization transitions in coupled networks comprise two different BA networks with four coupling probabilities p(0.1,0.4,0.8,1).
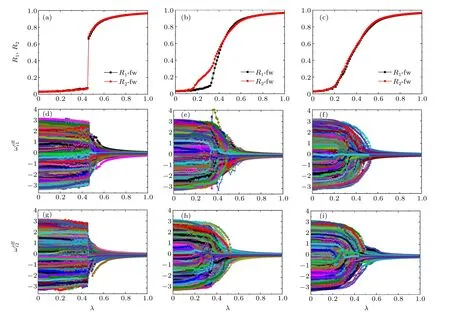
Fig. 2. Global order parameters R1 and R2 (top row), effective frequency (middle row), and effective frequency (bottom row) of nodes for three different coupling mechanisms when the increment of coupling strength δλ =0.01. The panels in the left, middle, and right columns represent assortative coupling,disassortative coupling,and anti-assortative coupling,respectively. Panels(a)-(c)show the global order parameters R1 and R2 versus the coupling strength λ during forward continuation. Panels(d)-(f)show the effective frequency versus the coupling strength λ during forward continuation of layer I.Panels(g)-(i)show the effective frequency versus the coupling strength λ during forward continuation of layer II.

Fig.3. Dependence of the global order parameters R1 and R2 on λ for three different coupling mechanisms during forward and backward continuation with coupling probability p=0.5. The three columns from left to right correspond to three different coupling mechanisms, assortative coupling, disassortative coupling, and anti-assortative coupling, respectively. The four rows (a)-(c), (d)-(f), (g)-(i), and (j)-(l) from top to bottom correspond to four different frequency distributions,the Gaussian distribution,Lorentzian distribution,Rayleigh distribution,and power-law distribution,respectively.


We pay particular attention to the influence on the dynamical transitions caused by several frequency distributions for the three different coupling mechanisms. All parameters studied in this part are consistent with Fig.1,except for frequency distributions and coupling probabilityp= 0.5. We choose two symmetric distributions,the Lorentzian and Gaussian distributions, and two asymmetric distributions, the power-law and Rayleigh distributions. Figure 3 shows the dependence ofR1,R2,andλduring forward and backward continuations for four different frequency distributions.The three columns from left to right correspond to assortative coupling, disassortative coupling,and anti-assortative coupling,respectively. The four rows from top to bottom correspond to the Gaussian,Lorentz,Rayleigh, and power-law distributions. It can be seen from Fig.3 that,except for the power-law distribution under assortative coupling in Fig. 3(j), other simulation results are basically consistent with those discussed above. In the assortative coupling mechanism,the simulation results show that the area of the hysteresis region is different from the explosion in Lorentzian,Gaussian,and Rayleigh distributions,but ES still occurs except for the power-law distribution. To explore the simulation results in Fig.3(j),we replaceδλ=0.01 by 0.001 and run the simulation again. The simulation results are consistent with Fig.3(j). Thus,we deduce that this is a characteristic phenomenon of assortative coupling because there are no negative numbers in the power-law distribution. In disassortative and anti-assortative coupling,the simulation results show that the phenomena of two different coupling mechanisms under different frequency distributions are consistent with the above.

Fig.4. Synchronization diagram for two-layer networks adopting different network topologies under three different coupling mechanisms. Panels(a)and(d)in the left,(b)and(e)in the middle,and(c)and(f)in the right columns represent assortative coupling,disassortative coupling,and anti-assortative coupling,respectively. The top and bottom rows represent coupled networks comprising BA and ER networks and coupled networks comprising two different ER networks. Networks of the same size and average degree are considered in both layers.
From the results presented above,we mainly focus on the phenomenon of synchronization in coupled networks. Here,we test the robustness of the scheme by changing the network structures in two-layer networks. For this purpose, we consider two different pairs of network structures and perform similar numerical experiments. In Figs.4(a)-4(c),we fix layer I to a BA network as studied above and fix layer II as a random ER network. These networks have the same network sizeNI=NII=1000 and the same average degree〈kI〉=〈kII〉=12.We use different network types to observe synchronization under three different coupling mechanisms with coupling probabilityp=0.5 for the two different layers by exploring the behavior of order parameters as a function ofλ. From a similar numerical experiment,figure 4 shows the variations of the order parameter in networks for forward and backward continuations. We can clearly see that ES occurs simultaneously in two layers under assortative coupling in Fig.4(a). The forward and backward critical coupling points of the two layers are the same, that is, the width of the hysteresis loop is the same. However,the area of the hysteresis loop in the BA network is obviously smaller than that in ER network. In addition, the two layers of networks show different synchronization phenomena than previous results for disassortative and anti-assortative coupling mechanisms. The nodes in both layers I and II under disassortative coupling show sudden synchronization due to sufficient coupling strength in Fig. 4(b).Under the anti-assortative coupling mechanism,a critical coupling strength of 0.377 appears. As the coupling strength increases to 0.377,the global order parameter of the BA network is larger than that of ER network. When the coupling strength reaches 0.377,the two-layer networks have the same global order parametersR1=R2=0.46 and when the coupling strength exceeds 0.377,the global order parameter of the BA network is smaller than that of ER network. As shows in Figs.4(d)-4(f),we fix layers I and II as two random ER networks with the same network sizeNI=NII=1000 and the same average degree〈kI〉=〈kII〉=12. The synchronization phenomena of the two-layer networks are equally obvious under the three different coupling mechanisms. In Figs.4(d)and 4(e),ES occurs in both layers,but the areas of the hysteresis regions are significantly different under assortative coupling and anti-assortative coupling mechanisms. There is also no ES for two-layer networks in Fig. 4(f). Therefore, the proposed scheme is quite robust and efficient,and can produce a rich variety of different synchronization phenomena.
4. Conclusion
In summary, we have investigated synchronization phenomena in coupled networks under three specific coupling mechanisms. The structure of the multiplex networks is determined by the intralayer connection and interlayer connection.Under the three coupling mechanisms proposed in this paper,the coupled networks exhibit rich synchronization phenomena.In addition, we have studied the synchronization of coupled networks under different frequency distributions. Under this strategy,the proposed scheme is also found to be robust and efficient in a multilayer network. The proposed synchronization models under different coupling mechanisms have potential significance for understanding the complex dynamics of realworld network systems,and may be suitable for designing the optimal coupling probability for synchronizing two-layer networks.This could lead to further ideas for multilayer networks and possible time and cost savings.
Acknowledgments
Project supported by the National Natural Science Foundation of China (Grants Nos. 71801066 and 71704046), the Natural Science Foundation of Anhui Province,China(Grant Nos. 1808085QG225 and 1908085MA22), the Fundamental Research Funds for the Central Universities, China (Grant Nos. JZ2020HGTB0021 and JZ2021HGTB0065), and the Outstanding Young Talent Support Program in Universities of Anhui Province in 2020 year.
- Chinese Physics B的其它文章
- Quantum walk search algorithm for multi-objective searching with iteration auto-controlling on hypercube
- Protecting geometric quantum discord via partially collapsing measurements of two qubits in multiple bosonic reservoirs
- Manipulating vortices in F =2 Bose-Einstein condensates through magnetic field and spin-orbit coupling
- Beating standard quantum limit via two-axis magnetic susceptibility measurement
- Neural-mechanism-driven image block encryption algorithm incorporating a hyperchaotic system and cloud model
- Anti-function solution of uniaxial anisotropic Stoner-Wohlfarth model

