求解一类投资组合模型的混合算法
郭文秀,张崇涛
(韶关学院 数学与统计学院,广东 韶关 512005)
Markowitz投资组合模型由Markowitz在1952年提出,该模型首次将统计方法应用到投资组合选择的研究中,使收益与风险的多目标优化达到最佳的平衡效果. Markowitz投资组合模型是著名的风险投资模型,在实际中有着广泛的应用,其建模过程以及求解方法一直都是学者们研究的热点[1-3].
按照Markowitz投资组合模型的观点,在收益和风险的权衡中,投资者要么在期望收益相同的条件下选择风险最小的投资策略,要么在风险相同的条件下选择期望收益最大的投资策略. 以第一个策略为例,Markowitz投资组合模型本质上是一个含有非负约束的二次规划问题,经过模系变换,其KKT条件[4]可以转化为一个绝对值方程的求解[5],这是笔者的研究对象.
绝对值方程在科学计算、工程等领域有着广泛的应用[6].对绝对值方程的数值算法设计是近年来学者们的研究热点.文献[7]通过利用光滑函数逼近模项构建了全局平方收敛的Newton法;文献[8]给出了一类广义的Gauss-Seidel迭代法;文献[9]利用一类特殊的线性搜索过程构建了Levenberg-Marquardt方法;文献[10]通过求解线性方程组和线性规划混合的方式建立了混合算法.
尽管绝对值方程本质上是线性的,但由于模项|x|的存在,求解常规线性方程组的一些高效算法并不能使用,如Krylov子空间迭代法.另一方面,如果能知道绝对值方程的解的分量符号信息,绝对值方程本质上就是一个线性方程组,这样对其应用线性方程组的高效数值算法即可明显提高计算效率. 本文在矩阵分裂迭代框架下提出一种聚类的技巧,用于获取绝对值方程的解的符号信息,进而构建混合数值算法,用以求解一类Markowitz投资组合模型,数值试验结果表明,聚类技巧的引入可以明显改善算法的收敛速度.
1 K-means聚类和矩阵分裂迭代混合算法
一般的绝对值方程数学定义如下:给定矩阵A,B∈Rn×n以及向量b∈Rn, 求向量x∈Rn,使得:

这里绝对值运算的定义为:|x|=(|x1|,|x2|,…,|xn|)T.
为了给出本文的混合算法,先给出一个引理.
引理1设绝对值方程的真实解为x*∈Rn,记x*分量的正、负和零指标集依次为η,ξ,ζ.那么式(2)成立:

这里Aηξ表示矩阵A分别以η,ξ为行、列指标的子矩阵.
证容易看出,存在一个置换矩阵P,使得:
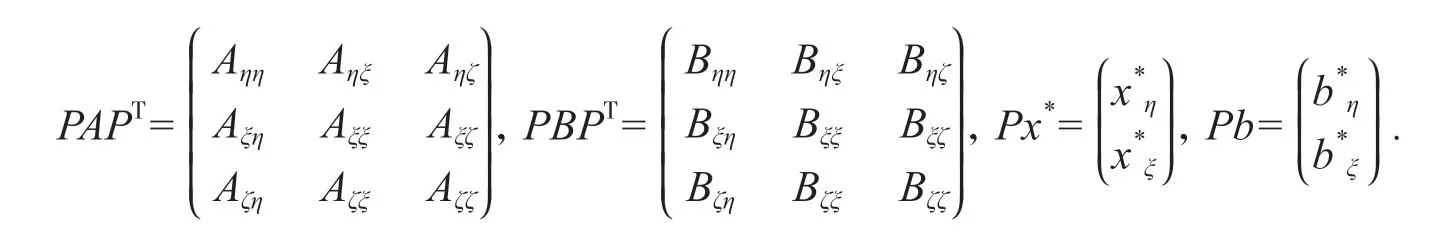
把上式代入Ax+B|x|=b,直接计算化简即可得到式(2).
由引理1的结果可见,只要能提前获取指标集η,ξ的信息,求解绝对值方程(1)即等价于求解线性方程组(2),此时可以采用求解线性方程组的高效数值算法. 但注意到η,ξ是由绝对值方程本身所决定的,理论上并不能在求解之前提前获取.为了克服这一困难,考虑采用全局收敛的矩阵分裂算法去获取符号指标的部分信息.
记x(t)表示某个全局收敛的矩阵分裂迭代法的第t步迭代近似向量,注意到:
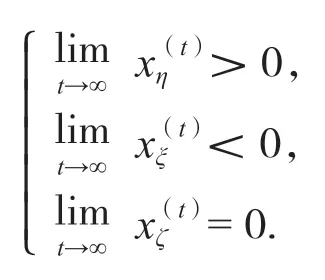
由于迭代是全局收敛的,因此当迭代步数t充分大时,应有xζ(t)≈0,则:
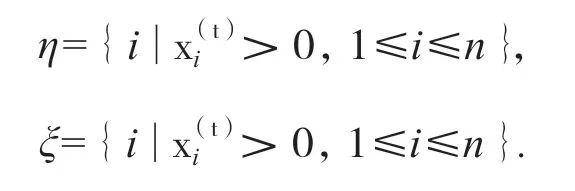
如果上述条件成立,有:

因此,式(3)可以看成是得到η,ξ的一个必要条件.
对于零元素的指标集ζ,注意到xζ(t)≈0,这表明:
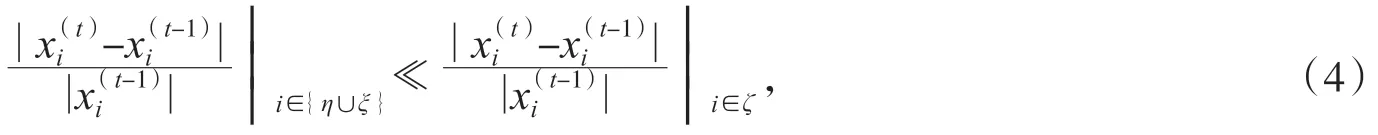
这里“≪”的意思是远远小于. 也就是说,条件(4)是获取ζ的一个必要条件. 因此,由条件(3),考虑引入聚类技巧在η,ξ中去获取ζ,这里采用K-means聚类方法把x(t)的分量指标分成2类.
综合上述讨论,可以给出K-means聚类和矩阵分裂迭代混合算法.
算法1K-means聚类和矩阵分裂迭代混合算法
(1)输入A,B,b,kmax,x(0).
(2)运行2步全局收敛的迭代算法得到近似迭代向量x(1),x(2). 初始化t=2.
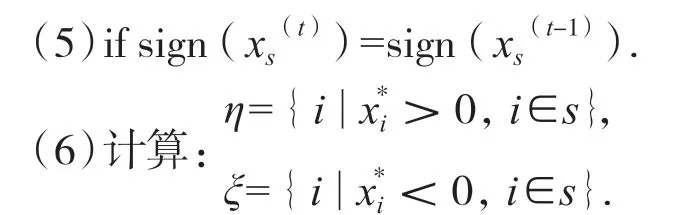
(8)如果残量误差是超线性收敛,取新的x(t+1)为下一步迭代向量;否则取旧的x(t+1)为下一步迭代向量.
(9)end if .
(10)如果迭代收敛,算法终止;否则t=t+1,回到(3).
对于算法1的细节,给出以下说明:
在第(2)步,为了充分利用绝对值方程的线性性质,选择基于矩阵分裂的迭代,即:

此处A=M-N表示矩阵A的一个分裂.
高职院校虽然对机制专业的改革做出了一些有益的探索,但人才培养模式单一,课程体系僵化,忽视了高职学生素质参差不齐的现实,不利于充分挖掘高职生的求知潜能,不利于高端技能型机械制造专门人才的培养。
第(4)步是基于式(4)所构建的,众所周知,K-means聚类的计算量不超过O(n2), 因此聚类技巧的引入不会增加整个算法的计算时间.
第(5)步中的sign表示对相应的向量各分量求符号.
第(6)~(7)步是根据式(3)所构建的,式(3)的成立可以保证当t充分大时第(8)步迭代向量更新策略的合理性.
如果聚类技巧不能发挥作用,算法1的最差情形也是退化为全局收敛的数值算法. 因此聚类技巧的引入不会降低原来算法的计算效率.
2 数值试验
本节先通过一个测试例子展示上节给出的聚类技巧的有效性,进一步把本文的算法应用到沪深股市光伏建筑一体化版块的Markowitz投资组合模型求解中.
例1考虑以下绝对值方程,设:
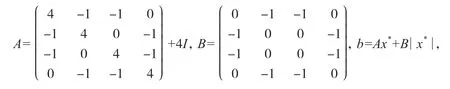
其中,为了便于观察混合算法运行结果的准确性,设定该绝对值方程的真实解为:x*=(-1,1,0,0)T.
在式(5)中使用Gauss-Seidel 迭代,即M=D-L,N=U.这里D,L和U。分别表示矩阵A的对角部分、严格下三角部分和严格上三角部分.令迭代初始向量x(0)=(1,1,1,1)T,停机准则设置为残量误差不大于10-5.
算法1的数值结果见表1.
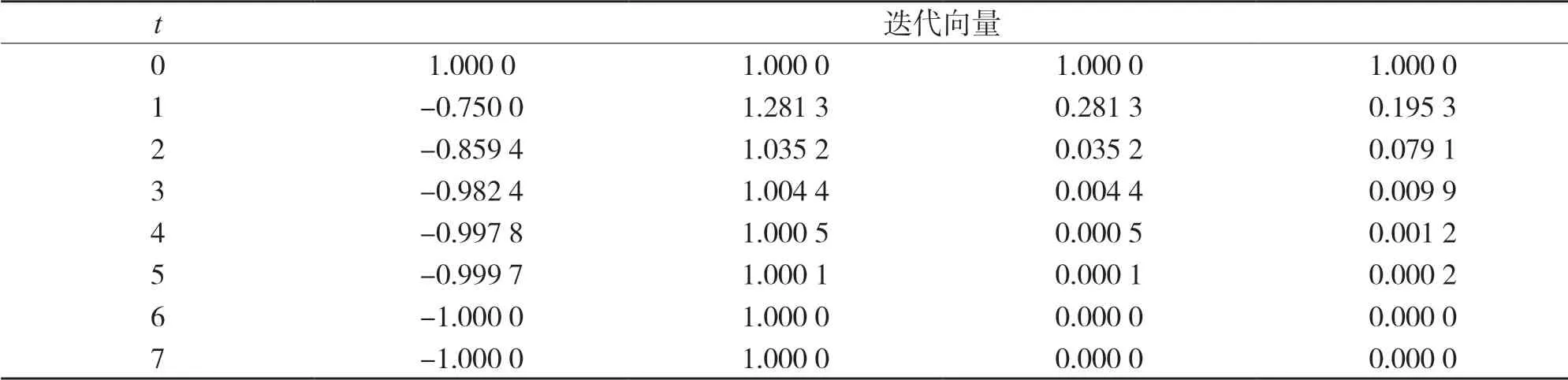
表1 例1的逐步迭代向量
Gauss-Seidel迭代在第7步达到了误差精度,通过观察迭代向量x(t)的各分量,可看出条件在第2步就已经满足了,这表明可以干预迭代过程使得该迭代提早终止(见表1).

表2 对yi(t)进行K-means聚类后例1的结果
应用聚类技巧以后,条件sign(x(t))=sign(x*)在迭代的第2步就已经满足了(见表2).另一方面, 随着迭代步数的增加,两个类的中心之间的距离越来越大,这表明聚类技巧发挥了作用.
例2考虑一类特殊的Markowitz投资组合模型,选取沪深股市光伏建筑一体化版块的37支股票在2019年6月-2021年5月期间的交易数据,通过计算个股的价格振幅并归一化得到37阶的协方差矩阵,进而可建立以下Markowitz投资组合模型:minwTQw,s.t eTw=1,rTw=ρ,w≥0.其中Q∈R37×37表示协方差矩阵,w∈R37表示对版块个股的投资权重向量,r∈R37表示个股的收益率期望,ρ∈R表示总收益,e∈R37是分量全为1的向量. 通过模系变换得到形如式(1)的绝对值方程,其中两个系统矩阵的结构为:
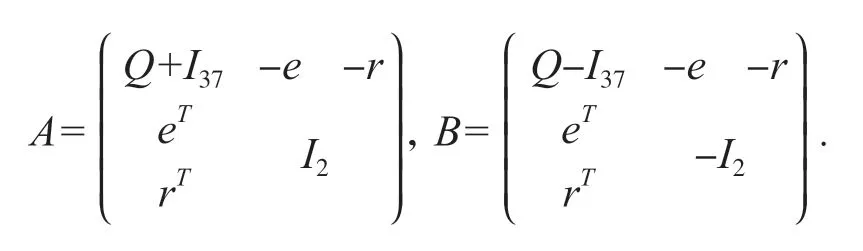
设置算法1的残量误差为10-5. 跟Gauss-Seidel迭代对比,例2的数值结果见表3.

表3 例2的结果
由表3可见,算法1比Gauss-Seidel迭代收敛更快, 这再次表明了聚类技巧的有效性.
3 结语
通过分析迭代向量的分量符号信息,应用K-means聚类分析技巧对求解绝对值方程的矩阵分裂迭代过程进行了加速,构建了混合算法. 在数值测试试验中,聚类技巧的应用是有效的,同时,笔者构建的算法还用于求解一类Markowitz投资组合模型,数值结果展现了混合算法的优越性.

