线性随机系统状态和参数鲁棒估计算法研究

耿跃峰

(许昌学院 电气与机械工程学院，河南 许昌 461000)

众所周知，工业中复杂的非线性系统一些物理参数很难确定，甚至有些参数完全未知，如某些部件的尺寸、泄漏系数、摩擦系数等等，这给系统的控制带来很大困难[1].复杂非线性系统的动态行为通常由一个具有时变参数的线性随机状态空间模型来描述[2].因此，需要同时获得参数和状态估计的方法.

卡尔曼滤波(KF)是目前最常用的一种滤波方法，均需要具有线性模型的实时卡尔曼滤波框架，在车辆控制[3]、疲劳检测[4]、网络安全[5]、机器人控制[6]等领域广泛应用.当模型参数与过程参数不匹配时卡尔曼滤波估计精度则会大大下降甚至发散.粒子滤波器(PF)是一种基于概率密度的点质量(或“粒子”)表示的序列蒙特卡罗法(SMC)联合状态参数估计技术，可应用于任何状态空间模型.PF的应用使得状态实时跟踪和未知系统参数准确识别成为可能[7].文献[8]提出一种序列蒙特卡罗联合状态和参数估计方法，能有效地处理参数突变.文献[9]把改进的卡尔曼滤波器应用于系统状态和参数估计.文献[10]研究了在存在高斯噪声的情况下非线性系统的联合参数状态估计.

但是非高斯噪声的存在会破坏线性递归算法的良好特性，因此需要设计一种对非高斯噪声不太敏感的鲁棒估计算法，对复杂系统状态和参数进行精确估计.为了追求精确的鲁棒估计，针对含有元件和传感器故障的线性随机时变系统，以MMF为基础，设计出一种鲁棒估计算法，对被研究系统的状态和参数进行联合估计.

1 线性随机时变系统的鲁棒估计算法

考虑的含有元件和传感器故障的线性随机时变系统为

x(k+1)=A(k)x(k)+B(k)u(k)+C(k)θ(k)+w(k)，

(1)

y(k)=D(k)x(k)+Γ(k)θ(k)+e(k)，

(2)

式中，x(k)∈Rn、θ(k)∈Rp分别是未知状态向量和参数向量，元件故障fC(k)=C(k)θ(k)，传感器故障fS(k)=Γ(k)θ(k)，并见图1.

从图(1)可以看出，系统未测量输出yS(k)在数学上可以描述为yS(k)=D(k)x(k).从实际的角度来看，对故障特征进行假设而不将其视为未知的时间函数是不合理的.因此线性随机系统参数变化的一般形式定义为θ(k+1)=Gθ(k)+η(k)，其中G是一个先验已知的非奇异矩阵，包含了所识别现象的先验信息.随机过程η(k)为零均值白噪声，其协方差矩阵Φ(k)为η(k):N(0,Φ(k)).系统输入向量和测量输出向量分别为u(k)∈Rm、y(k)∈Rr，一般情况下，A(k)、B(k)、C(k)、D(k)、Γ(k)已知且为具有适当维数的时变矩阵.假设过程噪声为零均值高斯白噪声w(k):N(0,Q(k))，其中Q(k)为协方差矩阵.测量噪声e(k)具有近似正态分布的非高斯分布[11].

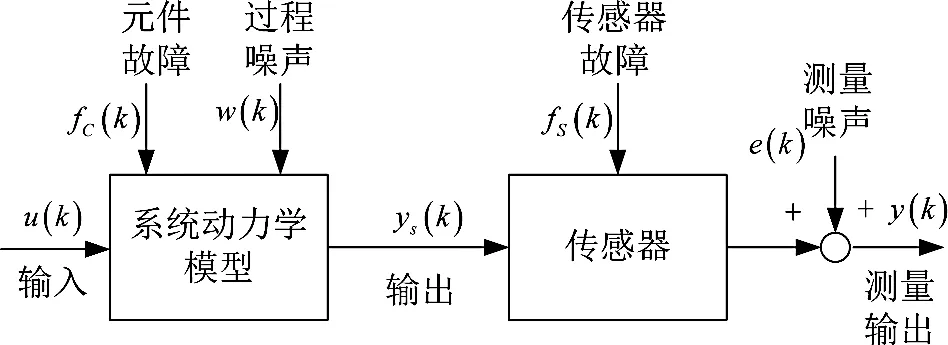
图1 研究系统

(3)

式中，概率密度p(e)表示首项概率密度p1(e):N(0,R1(k))和污染概率密度p2(e):N(0,R2(k))的集合，污染度ε的取值范围为0<ε<1，而R1(k)和R2(k)分别是非高斯分布公式(3)中首项和污染项的协方差矩阵.

对于系统(1)-(2)，对θ(k)和x(k)进行联合估计的简单方法是考虑扩展系统.

(4)

y(k)=H(k)z(k)+e(k)，

(5)

目标是在存在非高斯噪声时推导出线性随机系统状态和参数的鲁棒估计算法，并保持较低的灵敏度.Masreliez和Martin针对上述情况提出了鲁棒Kalman滤波器[12].与标准KF相比，当w(·)和v(·)具有高斯分布时，该滤波器对非高斯噪声的存在具有较小的灵敏度.扩展线性系统公式(4)和公式(5)的滤波方程为

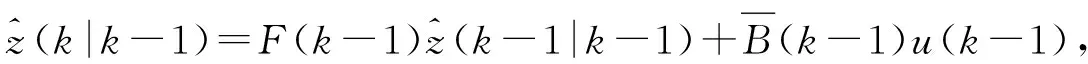
(6)

P(k|k-1)=F(k-1)P(k-1|k-1)FT(k-1)+Ξ(k-1)，

(7)

K(k)=PT(k|k-1)HT(k)TT(k)，

(8)

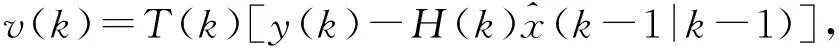
(9)

(10)

P(k|k)=P(k|k-1)-P(k|k-1)HT(k)T2(k)×H(k)P(k|k-1)Ef0{ψ′(v(k))}，

(11)

(12)

E(v(k))=T(k)E(ε(k))=0，

(13)

E(v2(k))=T2(k)[H(k)P(k|k-1)HT(k)+R1(k)]-1/2.

(14)

因此T(k)转换为

T(k)=[H(k)P(k|k-1)HT(k)+R1(k)]-1/2.

(15)

转换残差的协方差矩阵为I.

基于上述导出的方程，很容易地表示状态向量和参数向量的估计.

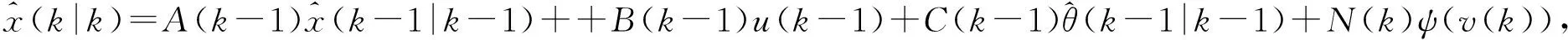
(16)

(17)

用这种方法导出了具有元件和传感器故障公式(1)和公式(2)的线性随机系统状态和参数的鲁棒估计算法.

2 实例仿真

将所研究算法应用于液压系统中进行验证，液压系统示意图如图2所示.将相关算法代入后，三种不同算法对液压伺服系统的状态估计、参数辨识以及污染值为ε1=ε2=0.15时的均方误差如图3、4所示.

图2 液压伺服系统示意图

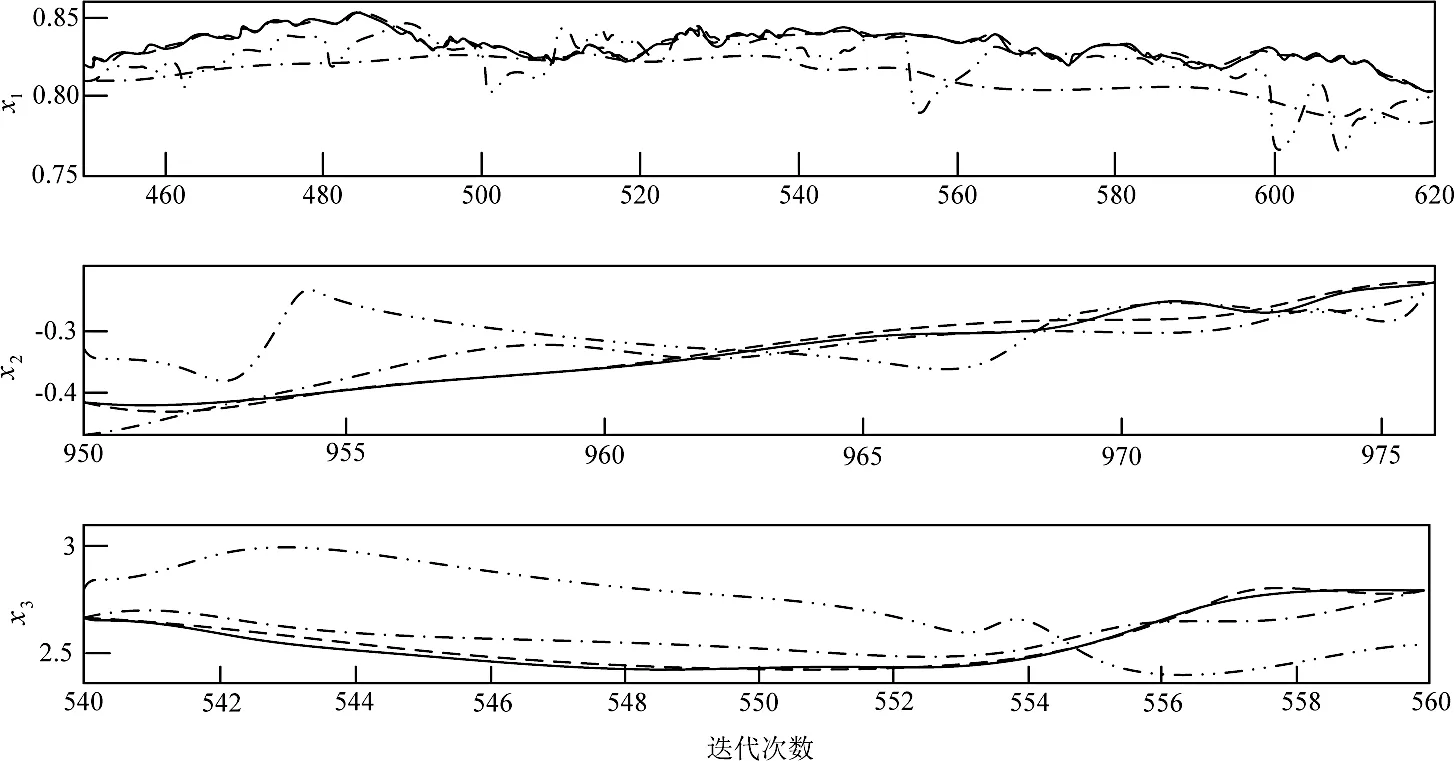
图3 状态估计

图3和图4分别为状态估计输出曲线和参数辨识输出曲线.在两个图中，实线、虚线、点划线、双点划线分别代表状态真值或参数真值、所提出的鲁棒估计算法、高斯混合粒子滤波算法、基于MMF联合算法.从图3中可知，所提出的鲁棒估计算法，能很好地跟踪伺服系统状态，从而得到状态的近似无偏估计值.而另外两种算法与系统状态真值误差较大.从图4中可以看出，所提出的鲁棒估计算法，可以对系统真值进行很好的辨识，而另外两种算法辨识输出与真值误差较多.图3和图4仿真结果表明，所提出的鲁棒估计算法对非高斯噪声和故障的存在敏感性较低，说明算法鲁棒性和容错能力较强.

为了更准确地说明所提出鲁棒估计算法(REA)的优越性，将其与扩展卡尔曼滤波器(EKF)、粒子滤波器(PF)、交互式多模型滤波器(IMMF)、高斯混合粒子滤波器(GMPF)、Masreliez-Martin滤波器(MMF)在迭代1 000次，污染度ε分别为0.05、0.1、0.2时的输出进行双比，具体结果见表1.

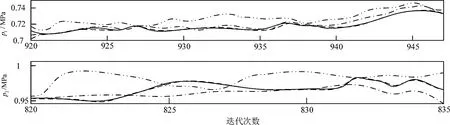
图4 参数辨识

表1 不同污染程度的均方误差

从表1可以看出，当污染度ε分别为0.15、0.26时，REA得到的最差结果分别为-3.832 1、-3.525 3，甚至优于其他算法得到的最佳结果(如EKF输出的-0.957 6、-0.921 0)，还有，REA输出值方差也远远低于其他算法.此外，从表1也可以看出，在有较高的污染程度时REA仍具有较低的方差.因此，从数据上说明了REA对非高斯噪声和故障的存在具有较低的敏感性和较好的鲁棒性.

3 结语

针对含有元件和传感器故障的线性随机时变系统，以Masreliez-Martin滤波器(MMF)为基础，提出了存在非高斯噪声时系统状态和参数鲁棒估计算法.通过液压伺服系统的例子，验证了所提出的鲁棒估计算法辨识得到的状态空间模型参数的效果.仿真结果表明，所提出的鲁棒估计算法能很好地辨识液压伺服系统状态和参数，并且当非高斯噪声出现时，所提出的鲁棒策略灵敏度低，从而证明了该算法优于其他如卡尔曼滤波器等，在存在元件和传感器故障值的随机线性时变系统中具有广泛的应用前景.