一类非线性时间分数阶扩散方程反问题的变分型正则化*

柳 冕，程 浩，石成鑫

（江南大学 理学院，江苏 无锡 214122）

引 言

近年来分数阶微分方程引起了数学、物理、化学、金融和水文等各个学科的广泛关注.相较于整数阶，分数阶微分算子具有非局部性，从而能更精准地模拟实际应用中具有记忆和遗传性质的模型.目前分数阶微分方程已经在分形理论[1]、随机游走[2]、高频金融数据[3]、黏弹性[4]和反常扩散[5]等各个领域取得了广泛应用.在反常扩散中，由于介质的复杂性如非均匀、各向异性介质等使得粒子的随机运动受到了限制，因而不能简单地通过均匀介质的标准统计方法来刻画，而分数阶扩散方程则能较为准确地模拟在异质多孔介质中表达反常扩散的真实模型.

分数阶扩散方程正问题已经获得了广泛的研究，包括有限元方法[6]、有限差分数值解法[7-8]以及解的存在唯一性研究[9]等，对于反问题的研究相对较少.很多文献都考虑过如下时间分数阶扩散方程反问题：

Murio[10]通过磨光正则化方法稳定求解了阶数γ=1/2时的情形，并给出了相应的收敛性分析.Cheng 等[11]利用迭代正则化方法得到了先验和后验参数选取规则下的误差估计.Liu 等[12-13]利用修改核方法研究了该问题，并分别给出了先验和后验假设下的收敛性分析.此外，Zheng 等[14]利用谱正则化方法得到了正则近似解与精确解之间的Hölder 型误差估计；Tuan 等[15-16]通过滤波正则化方法研究了该问题在不同源项的情形，并分别给出了收敛性分析.

上述问题研究的是一维半无限域情形，而在实际应用中，粒子扩散过程大多发生在空间非均匀环境中，特别是环境随着时间或空间位置变化而变化的情况，这就需要在研究的扩散方程中包含时空非均匀平流系数和非线性反应项.对于二维非线性分数阶扩散方程反问题的研究结果还相对较少，本文考虑如下问题：

这里a(·)表示与空间变量x相关的平流速度，F(x,y,t,u(x,y,t))是非线性源项，Dγt u(x,y,t)表示阶数为γ(0 ＜γ≤1)的Caputo 分数阶导数[17]，定义如下：

本文要研究的反问题是：假如a(x),F(x,y,t,u(x,y,t)), 终值φ(y,t)以及边界条件已知，来反演u(x,y,t),0≤x＜1的信息.

与一维的问题（1）类似，反问题（2）也是不适定的，这便导致我们无法稳定求解该问题，因而需要进行正则化方法求解.Vo 等[18]利用Fourier 截断正则化方法研究了该问题，并给出了误差估计.本文采用变分型正则化方法来稳定求解，将问题（2）转化成算子方程，并给出了三种变分形式.以罚项内函数G(ξ,s)=1为例，得到正则近似解与精确解之间的收敛性分析，并给出了数值仿真结果.

本文组织结构如下：第1 节，给出了一些辅助知识和基本假设；第2 节，给出了变分型正则近似解，同时给出了正则近似解的存在性与唯一性结果，并得到正则近似解与精确解之间的误差估计；第3 节，通过数值算例说明了方法的有效性；第4 节为本文的结论.

1 辅助知识

y＜0,t＜0R2

在本文中，我们将所有函数在时的值设为0，以此来将其拓展到 .

定义1设f是Lebesgue 可测函数，则

设u(x,·,·)∈L2(R2),x∈[0,1]是一个连续函数,则

C([0,1];L2(R2))={u(x,·,·):[0,1]→L2(R2)}

是一个有如下范数的Banach 空间：

f∈L2(R2)

定义2设，定义如下二维Fourier 变换：

引理1[17]设f∈L2(R2) ，γ ＞0，则

其中

引理2[19]假设α是一个正数且b＞a＞0，那么

在本文中，我们还将对问题（2）中的函数做如下假设：

(S1)：假设∃p＞0,q＞0，使得函数a(x)满足

(S2)：假设F是全局Lipschitz 函数，即对∀u,v∈R，∃k＞0，使得

(S3)：对于ε ＞0，我们假设测量数据φε∈L2(R2)与精确数据φ满足

‖φε-φ‖≤ε.

2 正则化方法和误差估计

容易看出非线性积分方程（5）包含了一些不稳定项.事实上，函数ψγ(x,ξ,s)的实部为，由此不难得到

这表明测量数据φ(y,t)的任何微小扰动都会导致解u(x,y,t),0≤x＜z＜1发生巨大变化，表明问题（2）是不适定的，因此需要通过正则化方法来恢复解的稳定性.

首先我们考虑问题（2）的齐次情形（F=0），即

对于固定的x，定义如下算子方程：

其中K:L2(R2)→L2(R2),u(x,y,t)→φ(y,t).

结合式（6）和算子方程（7）可得

为了稳定求解算子方程（7），我们构造了一个变分型正则近似解：

它等价于

其中*表示卷积，α是正则化参数，G(ξ,s)为罚项内函数.

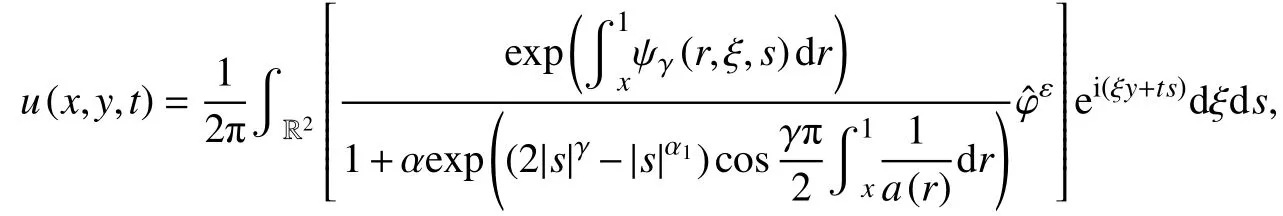
此时该方法为指数型变分正则化[20].

此时该方法为对数型变分正则化[21].

3） 特别地，当罚项内函数G(ξ,s)=1时，不难得到

该方法为Tikhonov 正则化.

以罚项内函数G(ξ,s)=1为例，类似上述求解齐次情形的方法推导问题（2），然而直接通过式（8）的求解过程很难得到正则近似解与精确解之间的误差估计.于是我们对其改进，并定义问题（2）的变分型正则近似解为

这里m＞1是一个常数.

2.1 解的存在唯一性

定理1假设函数a(x)与源项F分别满足假设(S1)和(S2)，那么积分方程(9)在C([0,1];L2(R2))上存在唯一解uα,ε.

证明对于任意的uα,ε∈C([0,1];L2(R2))，定义映射W:

W(uα,ε)(x,y,t)=uα,ε(x,y,t).

当w=1时，由引理2、假设(S1)和(S2)，则有

假设当w=n时,成立.

则当w=n+1时，

成立，从而

2.2 误差估计

定理2设u∈C([0,1];L2(R2))是问题（2）的唯一精确解，uα,ε∈C([0,1];L2(R2))是由式（9）给出的正则近似解，假如∃E＞0使得同时选取正则化参数其中m＞1，则可以得到如下误差估计：

证明由三角不等式，有

‖uα,ε-u‖≤‖uα,ε-uα‖+‖uα-u‖.

首先看第一项.根据引理2 和Parseval 等式，可以得到

下面我们分别估计G1和G2.

由Hölder 不等式，我们不难发现

由此我们可得

根据Grönwall 不等式，易得

所以

下面看三角不等式的第二项：

由此根据Grönwall 不等式，易得

所以

证毕.

3 数值算例

本节将通过数值算例验证变分型正则化方法对处理二维非线性时间分数阶平流扩散方程反问题的有效性.首先给出如下分数阶平流方程正问题：

如果

则我们可以得到正问题（10）的解如下：

测量数据 φε按如下方式得到：

φε(·,·)=φ(·,·)+ε·φ(·,·)·(2rand(size(φ(·,·)))-1),

其中ε反应相对误差水平.为了说明正则近似解的精确性，我们定义在点x0处的相对误差：

问题（2）的正则近似解由式（9）给出，其中

由于正则近似解带有非线性项，很难直接计算出正则近似解uα,ε(x,y,t)，采用如下的Picard 型迭代法进行计算：

数值计算中，我们取y∈[0,5],t∈[0,5]，相应的离散点数为M=21,N=21，步长分别为正则化参数由给出,其中m=2.

在图1 中，我们分别给出了精确解u和误差水平分别取ε=1E-1, 1E-2, 1E-3时的正则近似解在x=0处的数值结果.在图2 中，我们固定y=0，比较了在不同x取值下的数值结果.在表1 中，我们给出了不同误差水平下的相对误差.

从图1 可以看出，误差水平ε越大，正则近似解对精确解的逼近效果就越差；从图2 和表1 可以看出，随着x的增大，正则近似解的逼近效果也越好，这与理论结果相符合.

表1 不同误差水平下的相对误差ErTable 1 Relative errors corresponding to different error levels

图1 在x=0时的精确解和不同误差水平下的正则近似解uα,εFig.1 Exact solution u at x=0 and regularized approximate solution uα,ε curves corresponding to different error levels

图2 正则化解和精确解在不同x 取值下的比较(y=0)Fig.2 The exact solution and its regularized solution curves corresponding to different x values ( y =0)

4 结 论

变分正则化方法是求解数学物理方程反问题的一种有效方法，其中以经典的Tikhonov 正则化为代表.本文考虑了一类非线性时间分数阶扩散方程反问题，将不适定问题的求解转化成算子方程，给出三种不同的变分形式，即指数型变分正则化、对数型变分正则化和Tikhonov 正则化.以罚项内函数G(ξ,s)=1为例，对得到的正则近似解改进，并得到了正则近似解与精确解之间的收敛性分析.数值实验部分验证了所提方法的有效性.此外该方法还可推广到其他不适定问题，如非线性数学物理反问题和高维方程等情形，这有待于进一步研究.