矩形的特殊性,动点的不变性

广东省佛山市南海区里水镇和顺第一初级中学(528241) 陈有奋

1 题目呈现

如图1,在矩形ABCD中,AB=3,AD=4,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E,F.求PE+PF的值.

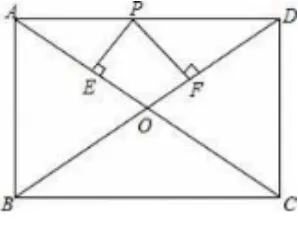
图1

本题来源于北师大版义务教育教科书九年级上册第一章“特殊平行四边形”第二节第三课时的课后练习题5.

2 教学价值

矩形的第三节课,是一节综合了性质与判定的练习课,而这一道题目侧重巩固矩形的特殊性质:对角线相等,同时,融入了动态的问题.在动态的过程中,需要学生抽象出本质的东西,找到变化中的不变量,再证明求解,培养逻辑推理能力.在矩形为背景的几何图形中,寻找求线段和的基本图形,培养几何直观素养.

3 功能分析

本题的其中一个条件是四边形ABCD是矩形,如何根据条件与结论找到矩形作用于本题的有效性质,是解决这道题目的关键因素之一,所以这道题目提供了特殊平行四边形性质运用的范例,也为如何抽取有效信息提供参考.

近年来,许多地方中考的压轴题都出现“动态问题”.学生对于动点问题,心理上存在畏惧.这需要平时教学循序渐进地进行动点问题的练习.而本题不存在多种情况的分类,适合学生建立动点问题的信心,建立“以静制动”的意识.

本题中所求线段为PE,PF都是垂线段,并且求PE+PF的值,这些都是几何题常见的问题:垂线段的用法,线段求和问题.通过本题,归纳出相关的方法.

4 教学措施——课堂呈现

4.1 给予充分的时间

这是一节练习课课后习题,由于题目具有较强的综合性,需要在课堂解决.对于能力强的学生应给出充足独立思考思想,老师不应该过多的干预,而对于数学基础较弱的学生应给予一定的帮助引导,让不同的层次的学生得到不同的发展.对于暂时找不到方法的同学,设计如下问题:

问题1.过点P分别作AC和BD的垂线这个条件应与题目的另一条件“矩形ABCD”怎么结合运用?

(关注矩形的对角线相等平分的性质,即OA=OD.)

问题2.条件中的垂直应如何应用? 垂直有哪些用法?

问题3.P点在运动,所求的两线段长度在变化,那么所求的和会变吗?

4.2 展示解题过程

课堂上各抒己见,百花齐放.同时要避免学生平铺直叙的分享自己的方法,不能引起其他学生的共鸣,所以要根据学生的方法适当的设计问题,引起大家的思考,从中体会不同的解题方法.

4.2.1 特殊值法

当P运动到AD的中点时,线段PE与PF的长度确定下来,并且两线段相等.然后可设AE为x,根据RtΔAPE和RtΔAOE勾股定理,以PE为等量关系建立方程.或者运用等面积法求得AE.

这种方法虽然不具有一般性,局限于选择填空题,但是动点问题,选择某个特殊的瞬间,这是以静制动的入门.

4.2.2 等面积法

由于本题不存在多种情况,所以我们可以选择P点在某一位置时,用静态的具体的图形研究问题,抽象出动态中的不变量.

运动过程中,矩形的相关的量是不变的,PE始终垂直于AC,PF垂直于BD(位置上的不变).当思路不明朗时,回忆垂直的用法(图2),通过排除,选择用等面积法.

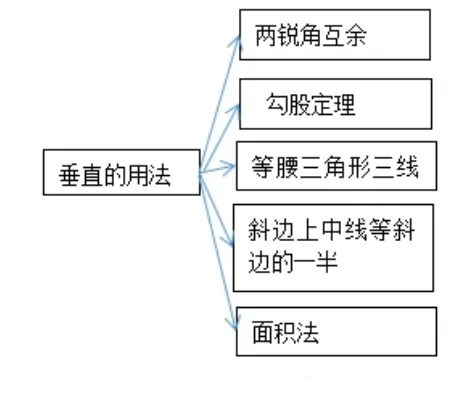
图2

PE是哪个三角形的高呢? (ΔAEP,ΔAOP,ΔACP)选择哪个三角形呢?

目的:通过设计问题,让学生思考解决问题的突破口.

ΔAEP的底边AE随着P的变化也在变化而另外两个三角形的底边AO,AC都没有变化,同时考虑另一以PF为高的三角形面积,ΔAPC和ΔBPD的面积,两者建立不了联系.所以选择用ΔAOP的面积建立PE的关系.

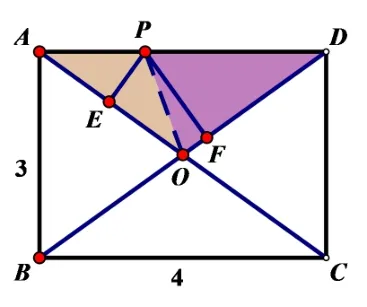
图3

本题在矩形的背景中运动,抽象出运动中垂直这一位置的不变性,联想到高,运用面积问题,发现两三角形面积相加为定值,根据对同一图形面积算二次的等面积法进行代数运算,由矩形的性质推导的OA=OB是出现PE+FF的关键,从而求得两线段之和.

4.2.3 极值法

生:根据求PE+PF的值,所以两线段之和为定值.把P无限的接近D点(图4),发现PF无限接近零,而PE的长度接近D到AC的距离.所以PE+PF的值为DE的长度.

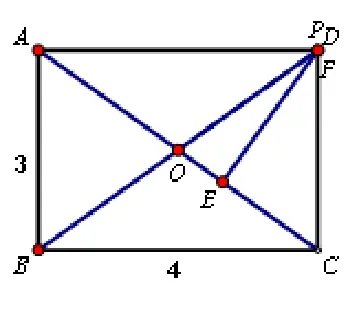
图4

对于初中学生而言,极值法比较抽象,难以理解.

师:怎么说明PE+PF就是D到AC的距离? 证明线段和等于有某一线段有哪些方法?

生:截长补短法.

给与学生思考新的求法.

4.2.4 截长法

生:过D作DI⊥AC,过P作PJ⊥DI(图5),根据三个角是直角的四边形是矩形,判定四边形PEIJ是矩形,所以PE=JI,相当于在DI上截取IJ=PE.只要证明DJ=PF即可.通过证明ΔPFE∽=ΔDJP.其中PD=PD,∠PFD=∠PJD=90°,根据PJ//EI,所以∠2=∠3,而OA=OD,所以∠1=∠3,所以∠1=∠2,全等可证.所以PE=JI,DI的长度为PE+PF的值.

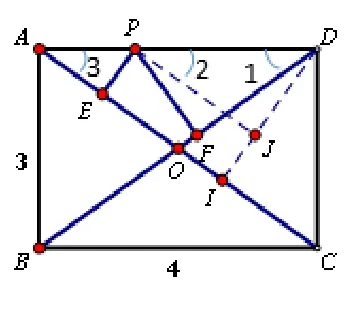
图5

师:P点在运动,始终有这个结论吗?

这个问题的提出是让学生再次感受以静制动是解决动点问题的关键.无论P运动在哪里,可以进行上述操作,矩形ABCD是不动的,矩形PEJI虽然在运动,却始终是矩形,PJ//EI是不变的关系,所以动态的PF=DJ.

4.2.5 补短法

生:延长EP到I使得PI=PF(图6),所以PE+PF就转化成PE+PI,也就是求IE的长度.连接ID.

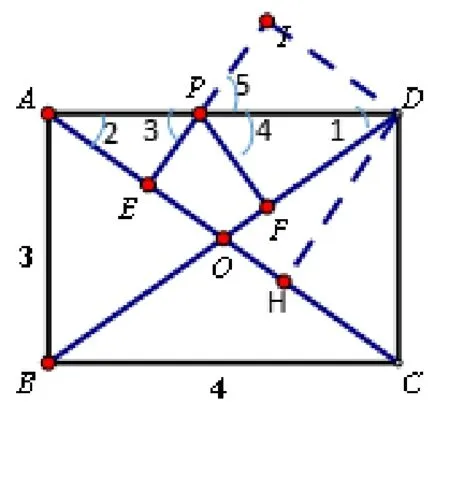
图6

师:为何想到连接ID.

生:因为延长PE后,我觉得是把ΔPFD通过AD对称到ΔPID,所以就连接DI,然后联想到∠I是直角.也就是所求的线段IE是ID,AC两平行线间的距离.过D作DH⊥AC,也产生了一个矩形IEHD,求IE的长度就是求DH的长度.

学生通过把PE进行补短法,把PE,PF放在同一线上,整个思维过程是一种直觉思维为主,如“感觉把ΔPFD通过AD对称到ΔPID,也就是要证明这两个三角形全等.我们还需进行逻辑推理.

由于OA=OD,∠1=∠2,ΔAPE和ΔPDF都是直角三角形,所以∠4=∠3,而∠3=∠5,从而∠4=∠5,PD=PD,PF=PI,所以ΔPFD∽=ΔPID,可得∠I是直角.

此方法是补短法,一开始,目标就很明确,而学生的“图形感”——图形的对称性,构造矩形等,这一系列的直觉思维为证明指出了方向,再根据矩形的性质进行严谨的逻辑推理,两种思维交替进行,这往往是解决综合性几何题常用的手段.

4.2.6 函数思想

4.3 各种方法小结

知识层面,上述的4 中方法,都用到了矩形的对角线相等的性质.这是有题目本身的条件所决.

方法层面,在动态中需要抽象出不变的量,绝对静态的不变量是矩形ABCD及其相关联的量,相对不变的量有PE⊥AO,PF⊥BO,以及在运动过程中,某一动态的线段或者角度始终跟另一量相等,从而建立数量关系.所以动态的题目需要“以静制动”,找到某个瞬间作为解题的图形,把问题转化为普通的几何题.

求线段的长度或者是求线段和的问题,本习题运用了等面积法,截长法,补短法等典型的方法,解题后的反思应从方法层面进行小结,让学生能够通过一道题目,衍生出多种解决问题的方法,实现以小胜多.本题是以矩形背景的动点题目,通过最后的结论,发现所求是一个定值,而整个运动并非围绕整个矩形展开,所以可让学生归纳出一般性的结论:等腰三角形的边上的一点,到两腰的距离之和为一定值,这一定值等于一腰上的高.

由抽象的动点问题到某个瞬间的静态几何图形,再由具体到一般的归纳,使整道题目上升到一个结论的高度,培养学生的抽象能力,语言表达能力,使学生透过运动的表象看到了本质属性.

4.4 以变促巩固

如图7,在矩形ABCD中,已知AD=4,AB=3,点P是射线AD上的一点,当P经过点D后,PE⊥AC,PF⊥BD,E,F分别是垂足,求PE-PF的值.

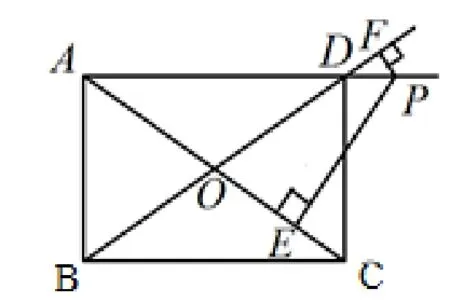
图7

此变式既源于本题又高于本题,上述的所归纳的知识层面和方法层面,都可以在变式题中再次运用.同时变式题的构图比原题稍复杂,原题是“加法”(面积和,线段和),变式是“减法”.不是一味地照搬,而是把原题的方法进行迁移,培养学生灵活运用知识与方法.

5 教学反思

通过题目的条件以及图形的位置关系,结合特殊图形(如本题的矩形)的性质,能迅速联想到其所需的性质,这正是思维敏捷性的体现,并与题目相关条件进行有机结合,这是提高解题能力的关键.

本题通过一题多解,对于求线段和的问题,建立不同的方法,通过条件的不同的组合建立起与结论的关系,这个过程就是推理的不同表现形式,有利于学生通过同一知识的不同求法建立这一问题的知识体系,提高学生的推理能力.

从不用的方法中,体现了同一知识间的相互转化,如本题中的动点问题的处理,虽然方法有所不同,却是同样概括运动中的不变量,归纳出不同方法间的共性,从不同解题方法中培养学生的概括能力.

学生能力的提升并非一蹴而就,必须充分发挥例习题的功能,而不仅仅是知识层面上的巩固,更应该从每道题目中都要有所收获,能力在潜移默化中提升.