利用相似日小波变换和多层感知机的短期光伏功率预测

陈辉煌，陈志聪，吴丽君，程树英，林培杰

(福州大学物理与信息工程学院，微纳器件与太阳能电池研究所，福建 福州 350108)

0 引言

近年来，太阳能因其清洁、无污染、丰富和取之不尽的特性受到广泛关注[1-2]. 根据国际能源署(IEA)发布的报告，到2019年底，全球光伏系统的装机容量至少为627 GW，其中2019年为115 GW[3]. 然而，太阳能的不确定性、间歇性、波动性和不可控性不利于电网的安全稳定运行，阻碍了光伏发电的大规模应用. 准确预测光伏功率是光伏系统大规模应用和电网合理规划的前提，通过预测光伏发电量，可以提前配置电网，减少太阳能波动对电网的影响[4-5].

根据使用原理可以将光伏功率预测方法分为物理方法和统计方法两类. 物理方法首先根据物理公式建立电厂的物理模型，然后将通过数值天气预报获得的气象数据代入模型以预测发电厂的功率，它无需历史数据，并且可以在电厂实际建设之前获得电力预测值[6-7]. 但是，该方法在模型构建过程中需要考虑许多因素，比如： 电厂设备本身的参数、电厂设备的老化、外部环境的影响等，这使得建模工作变得困难，而且模型的抗干扰能力和鲁棒性也较差[8]. 统计方法基于光伏电站的历史数据，通过相关分析、参数估计和曲线拟合来建立预测模型，而对光伏系统的复杂光电转换过程不需要有清晰完整的理解，与物理方法相比，它具有建模简单、通用性强的优点[9].

传统的统计方法常用的技术有时间序列法[10-11]、模糊逻辑法[12]、回归分析法[13-15]和马尔可夫链法[16]. 时间序列分析基于系统观测获得的时间序列数据，通过曲线拟合和参数估计(例如非线性最小二乘)建立数学模型，可以从时间序列中找出变量的特征和发展规律，从而有效预测变量的未来趋势. 缺点是随着时间尺度和输出维度的增加，预测结果将变差. 模糊逻辑模仿了人脑的不确定性概念判断和推理思维方式，实现了模糊综合判断，解决了传统方法难以处理的常规模糊信息问题，不需要建立研究对象的精确数学模型，从而使模型简单，易于被接受、理解和应用. 缺点是为复杂系统建立模糊规则和隶属函数非常困难且耗时. 回归分析利用数据统计原理处理大量统计数据，确定因变量与一些自变量之间的相关性，建立具有良好相关性的回归方程，可用于预测因变量的未来变化. 但是，回归方程的形式只是一种推测，这使回归模型的可靠性在某些情况下降低了. 马尔可夫链是一种典型的随机过程，模型的当前状态仅与其前一时刻的状态有关，它使用转移概率矩阵来预测系统的状态及其发展趋势，尽管某些情况下它可以很好地预测系统状态，但并不适用于中长期预测.

基于人工智能算法的新型统计方法可有效克服传统统计方法的缺陷[17-20]. 人工智能模型可以提取高维复杂非线性特征并将其直接映射到输出，与物理模型和传统统计模型相比，它在预测准确性、稳定性、通用性等方面都有很大的进步[21-23]. 但是，目前的大多数研究没有充分结合不同算法的优点，这限制了预测的准确性. 针对这一问题，本研究基于相似日小波变换和多层感知机(wavelet transform on similar days and multilayer perceptron, WTSD-MLP)建立智能光伏功率预测模型，它将小波变换的多分辨率特点和多层感知机(multilayer perceptron, MLP)的非线性拟合能力结合起来，有效地提高了预报的可靠性. 首先，选取相似日数据并归一化，然后使用小波变换对数据进行预处理. 其次，训练多层感知机模型学习气象因素与光伏功率之间的映射关系，使用的训练算法为自适应矩估计算法. 最后，基于沙漠知识澳大利亚太阳能中心(DKASC)的大型数据集[24]验证所提模型的有效性. DKASC于2008年开始运营，位于澳大利亚中部一个拥有丰富太阳能资源的沙漠小镇，是一个光伏电池类型丰富的太阳能技术示范基地.

1 总体方案介绍

图1 设计的总体框图Fig.1 Overall block diagram of the design

为提高光伏功率预测的准确性，本研究将小波变换的多分辨率特点和多层感知机的非线性拟合能力结合起来，提出基于相似日小波变换和多层感知机的新型光伏功率预测模型. 实验过程分为4个步骤：

1) 根据全局水平辐照度的欧氏距离选取相似日数据并归一化，然后使用小波变换对数据进行预处理，将气象因素和光伏功率数据分解成一组分量信号，即近似信号和多个细节信号.

2) 训练多层感知机模型学习气象因素分量信号与对应光伏功率分量信号之间的映射关系，使用这组模型在预测时可以获得光伏功率各个分量信号的预测值，然后再进行信号重构，即对所有预测分量进行求和，其中，气象因素为模型输入，光伏功率为模型输出，且使用的训练算法为自适应矩估计算法.

3) 使用训练好的模型来预测测试集.

4) 使用平均绝对误差、平均偏差误差、均方根误差等6个指标进行模型性能评估和误差分析，以反映模型综合性能.

设计的总体方案如图1所示.

2 数据集预处理

2.1 沙漠知识澳大利亚太阳能中心数据介绍

DKASC位于澳大利亚北领地爱丽丝泉(Alice Springs)的沙漠知识区，该技术基地的太阳能发电设备包含38个站点, 具体信息详见文献[24]. 以22号光伏电站(容量为16.8 kW)为研究对象，其详细信息如表1所示. 自2010/11/8的0:00:00起，电厂数据系统全天连续记录，每5 min记录一个数据点，本研究下载的数据截至2018/11/18的3:45:00. 数据包含电气参数，如所接收的有功电能(kW·h)、电流相位平均(A)、有功功率(kW)，以及相关气象因素.

表1 22号光伏电站的详细信息

2.2 输入气象因素选择

光伏电池是利用光伏效应将太阳辐射转化为电能的设备[25]，其发电量主要受辐照度和温度的影响，此外，还有许多其他因素会间接影响光伏发电，例如风速、风向、相对湿度和每日降雨量. 尽管这些因素将在不同程度上影响光伏电站的电力，但如果考虑所有因素，模型的复杂性将会增加，也难以确保这些数据的完整性. 本研究通过计算Spearman相关系数来选择最佳输入气象因素，即计算气象因素和光伏功率之间的Spearman相关系数，选择最为相关的4个气象因素作为模型的输入，其计算方式如下：

1) 将两个N维列向量X和Y对应的元素Xi和Yi转换为在各自列向量中的排名，记为R(Xi)和R(Yi)；

2) 根据

(1)

计算两个列向量X和Y中对应元素的R(Xi)和R(Yi)之间的绝对差异di，并相加得到d；

3) 根据

(2)

计算出两个列向量之间的相关性Rs.

使用2018年的光伏电站数据进行计算，气象因素和光伏功率之间的Spearman相关系数为: 风速NaN; 温度为0.216; 相对湿度为-0.348; 全局水平辐照度为0.834; 散射水平辐照度为0.334; 风向为0.002; 日降雨量为-0.185. 其中，由于该年风速数据全部缺失，无法计算风速的Spearman相关系数. 所以，与光伏功率最为相关的四种气象因素为： 全局水平辐照度、相对湿度、散射水平辐照度和温度.

2.3 相似日选择

在许多研究中[26-27]，相似日法被认为是提高短期功率预测准确性的有效预处理步骤. 在此过程中，选择相似日的依据至关重要. 根据2.2节中的演算，选择与光伏功率最为相关的全局水平辐照度作为选择相似日的依据. 通过计算测试集与训练集之间全局水平辐照度的欧式距离，选择训练集中欧式距离最小的前80%数据作为新的训练集. 欧氏距离的计算如下式所示.

(3)

其中：d是欧氏距离；X1和X2是离散序列，即全局水平辐照度序列；N是样本数.

2.4 数据归一化

由于光伏功率及各种气象因素的单位各不相同，并且取值范围变化很大，因此需要进行归一化以减少误差. 归一化公式为：

(4)

其中：y为归一化后的变量，ymax=1，ymin=0；x为光伏功率或各种气象因素.

2.5 小波变换

小波变换继承和发展了短时傅里叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间-频率”窗口，是进行信号时频分析和处理的理想工具. 采用Biorthogonal小波系中的bior 6.8对数据进行预处理，这个系列的小波函数具有线性相位性，主要应用在信号与图像的重构中，利用其将气象因素和光伏功率数据分解成一组分量信号，即近似信号和多个细节信号.

3 基于多层感知机的光伏功率预测建模

3.1 多层感知机及自适应矩估计算法简介

多层感知机在单层神经网络的基础上引入了一到多个隐藏层. 隐藏层位于输入层和输出层之间，单隐藏层的多层感知机结构如图2所示. 多层感知机的参数通过监督学习进行调整，分为两个步骤： 正向传播和反向传播. 正向传播的公式如下式所示.

图2 多层感知机的结构Fig.2 The structure of multilayer perceptron

ot=g(Vht)

(6)

其中：U和V为权重矩阵；xt是t时刻的输入向量；ht是t时刻的隐藏层输出向量；ot是多层感知机在t时刻的输出向量；g(·)是输出层的激活函数，通常选择线性函数；f(·)是隐藏层的激活函数，通常选择Sigmoid函数，其表达式为：

f(x)=Sigmoid(x)=1×(1+exp(-x))-1

(7)

考虑到功率不会为负，输出层将在训练和预测期间选择不同的激活函数，在训练期间将选择线性函数，而预测期间将选择正线性函数，如下式所示.

(8)

自适应矩估计算法[28]是一种对随机梯度下降法的扩展，在计算机视觉和自然语言处理的深度学习模型中得到了广泛应用. 它与经典的随机梯度下降法是不同的，随机梯度下降保持一个单一的学习速率，用于所有的权重更新，并且在训练过程中学习速率不会改变； 而自适应矩估计算法的每一个网络权重都保持一个学习速率，并随着学习的展开而单独地进行调整，该方法利用梯度的一阶矩和二阶矩计算不同参数的自适应学习速率.

3.2 模型配置

为了验证所提基于相似日小波变换和多层感知机的功率预测模型的有效性，将其与普通多层感知机(MLP)[29]、小波神经网络(wavelet neural network, WNN)[30]、长短期记忆网络(long short-term memory, LSTM)[31]、小波粒子群优化支持向量机(wavelet, particle swarm optimization and support vector machine, Wavelet-PSO-SVM)[2]及蚁群优化Elman神经网络(ant colony optimization algorithm and Elman neural network, ACOA-Elman)[20]进行了对比. 通过对气象因素的分析，可知模型的输入气象因素为4种，所以输入层神经元数为4，输出层神经元数为1. WTSD-MLP、MLP和WNN的隐层数为3，隐层神经元数为64； ACOA-Elman的隐层数为2，隐层神经元数为8. 损失函数为均方误差MSE，训练迭代次数为100. WTSD-MLP、MLP、WNN和LSTM的训练算法为自适应矩估计算法(该算法有3个内部参数：β1和β2为指数衰减率，其值分别是0.9和0.999；ε为一个避免除以零而使用的小数，通常为10-8)； ACOA-Elman的训练算法为量化共轭梯度法.

4 实验验证

4.1 性能指标

平均绝对误差(mean absolute error, MAE)、平均偏差误差(mean bias error, MBE)、均方根误差(root mean square error, RMSE)、平均绝对百分比误差(mean absolute percentage error, MAPE)、皮尔逊系数(R2)和技能得分(skill score, SS)来评估模型的性能，如下所示.

(9)

其中：Ppred是预测功率；Pmeas是实测功率；N是样本数；P0是发电厂的容量； MAE0是基准模型的平均绝对误差； MBE0是基准模型的平均偏差误差； RMSE0是基准模型的均方根误差； MAE1是对比模型的平均绝对误差； MBE1是对比模型的平均偏差误差； RMSE1是对比模型的均方根误差； 且基准模型为普通多层感知机，对比模型为包含本文所提模型在内的另外五种模型.

4.2 实验结果

为了验证本模型的有效性，以DKASC的22号光伏电站为研究对象进行了对比实验，将数据集分为两类： 训练集和测试集. 考虑到光伏电池将随着时间的流逝而老化，本实验使用2018年的数据更真实地反映光伏电站的最新状态. 随机选择测试集如下： 春天选择2018/09/29； 夏天选择2018/02/08； 秋天选择2018/05/21； 冬天选择2018/08/21. 并将测试集之前20 d的白天数据(6:00—19:00)选择为训练集. 通常，预测分辨率为15 min可以满足市场需求，因此上述数据的时间间隔为15 min. 四个季节的光伏功率预测结果曲线图如图3所示，对应的误差详细信息如表2所示.

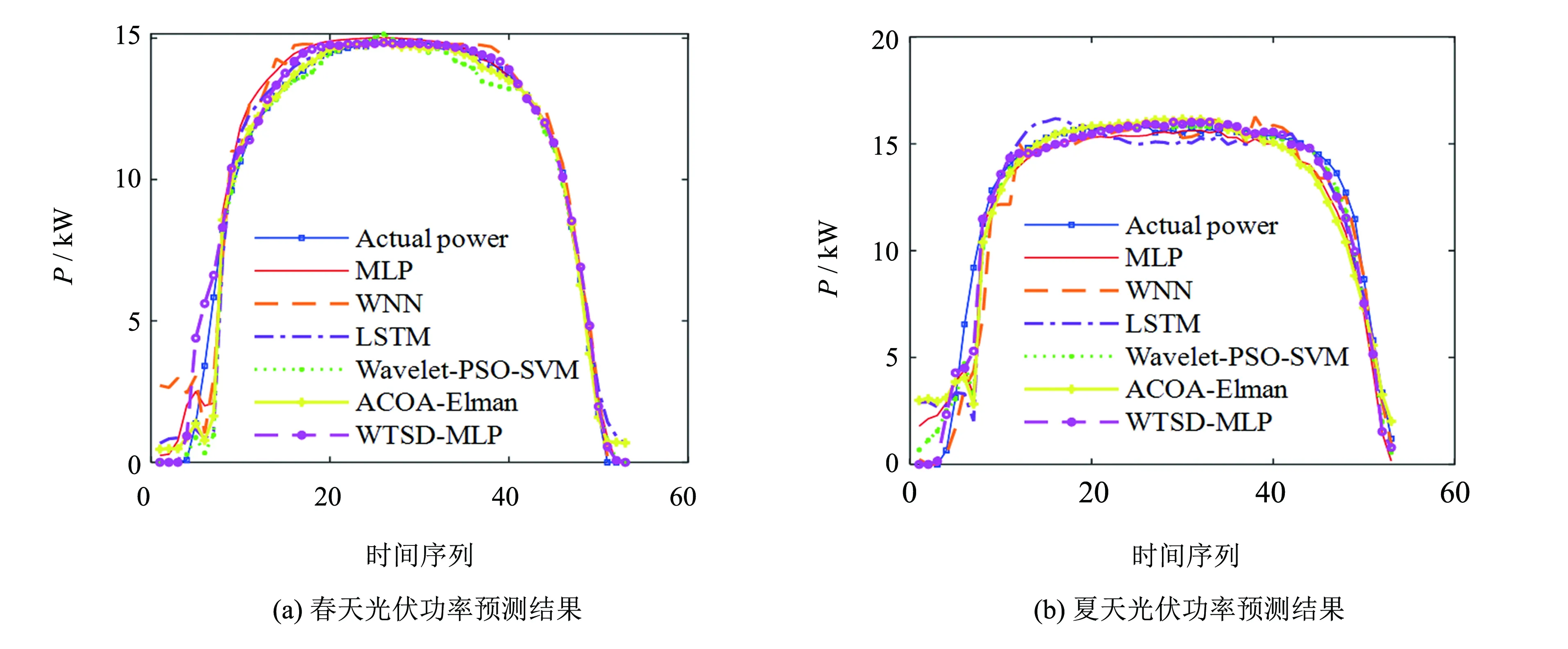
图3 四个季节的光伏功率预测结果曲线Fig.3 PV power forecast results in four seasons

表2 四个季节下六种模型光伏功率预测的实验结果

从表2中的实验结果可知，对于典型的指标RMSE，MLP模型为0.128～1.308 kW，平均为0.783 kW； WNN模型为0.136～1.159 kW，平均为0.793 kW； LSTM模型为0.208～1.445 kW，平均为 0.847 kW； Wavelet-PSO-SVM模型为0.132～1.045 kW，平均为0.674 kW； ACOA-Elman模型为0.144～1.467 kW，平均为0.883 kW； WTSD-MLP模型为0.103～0.836 kW，平均为0.538 kW. 对于结合了MAE、MBE和RMSE三者的综合评价指标SS，MLP模型为基准模型，所以为0； WNN模型为-0.402～0.172，平均为-0.001； LSTM模型为-0.607～0.095，平均为-0.101； Wavelet-PSO-SVM模型为0.033～0.340，平均为0.170； ACOA-Elman模型为-0.312～0.272，平均为0.045； WTSD-MLP模型为0.221～0.427，平均为0.284. 综上所述，本模型总体预测效果要好于其他的对比模型，从SS来看，相较于MLP、WNN、LSTM、Wavelet-PSO-SVM和ACOA-Elman平均分别改善了28.4%、28.5%、38.5%、11.4%和23.9%.

5 结语

基于相似日小波变换和多层感知机建立了以15 min为间隔的短期光伏功率预测模型. 首先，选取相似日数据并归一化，然后使用小波变换对数据进行预处理. 其次，训练多层感知机模型学习气象因素与光伏功率之间的映射关系，使用的训练算法为自适应矩估计算法. 最后，为了验证所提出模型的有效性，基于沙漠知识澳大利亚太阳能中心的实际大型数据集，将所提出的模型与基于多层感知机、小波神经网络和长短期记忆网络的其他预测模型进行了比较. 实验结果中的技能得分表明，本预测模型相较于多层感知机、小波神经网络、长短期记忆网络、Wavelet-PSO-SVM和ACOA-Elman平均分别改善了28.4%、28.5%、38.5%、11.4%和23.9%，在预测准确性和可靠性方面具有更好的性能.