从直观想象到逻辑抽象: 基于GeoGebra的立体几何教学




【摘 要】立体几何的教学,需要引导学生在直观感知、操作确认中发展空间想象能力,在度量计算、推理论证中提升逻辑抽象能力。以GeoGebra为平台的立体几何教学,可以创设情境,为概念理解提供直观;变换视角,为问题解决寻求路径;联系推理,为规律论证启发思路;交流分享,为自主学习创造机会。
【关键词】立体几何;GeoGebra;数学教学;直观想象;逻辑抽象
【中图分类号】G633.6 【文献标志码】A 【文章編号】1005-6009(2022)27-0015-04
【作者简介】张加红,江苏省常州市田家炳高级中学(江苏常州,213001)教师,高级教师,江苏省首届师德模范,江苏省“五一劳动奖章”获得者。
立体几何是研究现实世界中物体的形状、大小与位置关系的,虽然三维世界更贴近生活实际,但囿于空间想象力和表达手段的欠缺,尤其是空间图形的平面表达(直观图)的制约,立体几何一直是高中数学教与学的难点。《普通高中数学课程标准(2017年版2020年修订)》强调要让学生学会“运用直观感知、操作确认、推理论证、度量计算等认识和探索空间图形的性质,建立空间观念”[1],这就需要发挥信息技术的动态可视化特性。
作为一款专为教与学而设计的动态数学软件,GeoGebra内嵌计算代数系统和指令输入方式,可以对几何对象进行直接代数化处理,使数学教学更为方便快捷,从而实现“形”(Geometry)与“数”(Algebra)的完美融合,可以说“懂得GeoGebra,她就给你独到眼光,让你洞悉数学世界”[2]。
对应立体几何的教与学,GeoGebra有专门的 3D Graphics绘图区。在这一绘图区,我们可以构建逼真的三维几何体,并呈现不同视角下的线面位置关系(在几何体旋转滚动的过程中,线面自动虚实切换),构建“多元联系表征”的立体数学情境,并且可以突破表象的制约深入学科内部洞悉数学本质,从而实现从直观形象到逻辑抽象的升级。
本文以GeoGebra为平台,通过具体的教学案例呈现从“形”到“数”的探索,从而破解立体几何教学难点,提高学生的学科素养。
一、创设情境,为概念理解提供直观
数学本质上是对概念的理解和运用,立体几何中也有很多概念,但这些概念多是以柱、锥、台、球等空间几何体为载体而生成的。因此,“通过丰富的实物模型或利用计算机软件呈现空间几何体,帮助学生认识它们的结构特征”成为我们的重要任务。
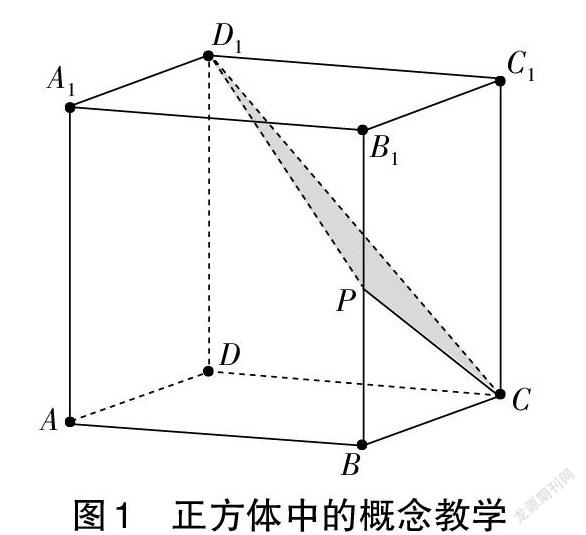
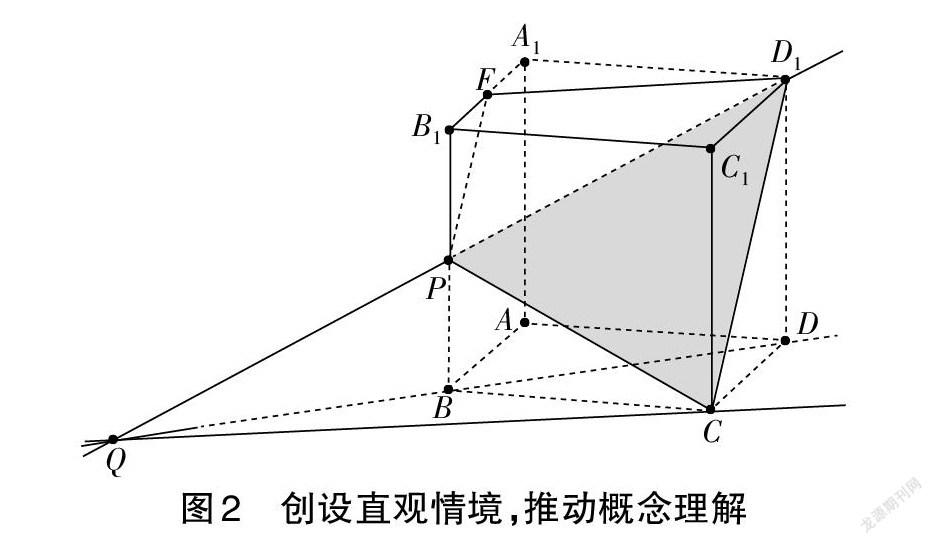
如教学异面直线的概念时,可以以图1中正方体ABCD-A1B1C1D1(P为BB1的中点)为载体,展示棱之间的位置关系,引导学生发现相交、平行之外的另外一种关系——异面;辨析D1P、DB间的位置关系,可提炼出异面直线的概念(不同时处在任何一个平面内的两条直线)。以空间图形为背景来学习概念,因有具体的样例支持而容易被学生接受。但这样的教学也可能会因视觉受限而造成学生的思维障碍,如图1中很多学生会误以为D1P和AB相交。此时,教师可以利用GeoGebra创设更加直观的情境,拖曳改变正方体的位置(见图2),避免因视角受限而导致的错误理解。因此,立体几何需要的是动态的直观背景,以突破“横看成岭侧成峰,远近高低各不同”的视觉障碍。在此基础上,对平面D1CP的认识应突破三角形的限制,也不限于等腰梯形D1CPF,而应在整个平面内构造平面D1CP与平面ABCD的交线——延长D1P、DB相交于点Q,QC即为两平面的交线。
立体几何的学习离不开图形,考虑到空间图形平面表示(直观图)的局限性,用信息技术来描述问题、理解概念、解决问题便显得尤为重要。GeoGebra 3D Graphics绘图区就是为立体几何教学量身定制的软件平台,通过它能构建动态的直观情境,不仅为概念生成提供丰富的样例,更为概念理解提供想象空间。而空间观念正是在这样的“可视化”感知中得以落实,从而真正培养学生的数学思维,提高学生解决问题的能力。
二、变换视角,为问题解决寻求路径
数学学科中,没有方法就没法解题,如何掌握数学解题的方法?张景中院士提出教育数学三原理,即“在学生头脑里找概念,从概念里产生方法,方法要形成模式”[3]。对立体几何的教学亦是如此,概念要能迅速转化为方法,需要让学生认识到问题的全貌,从而从整体上认识问题,在比较中找到最合理、最简捷的解题路径。
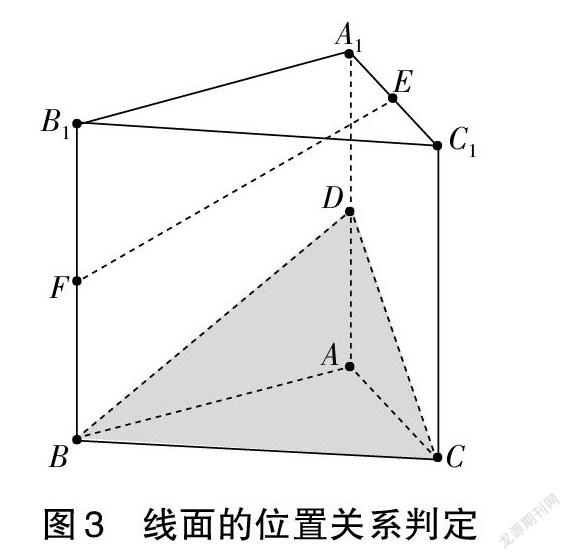
例1(线面的位置关系判定):如图3,三棱柱ABC-A1B1C1中,D、E、F分别为棱A1A、A1C1、B1B的中点,试判断直线EF与平面BCD的位置关系。
对照线面相交、线面平行的概念,判断直线EF与平面BCD的位置关系的关键在于“在平面BCD内找到一条直线l与EF平行或相交”,而直线l与EF构成了另一平面α,因此解题的方向在于构造平面α。于是便有了图4所示的解题路径,构造平面BFE,与CD交于点M,因为EM∥FB且EM≠FB,可知EF与MB相交,这样就可以说明直线EF与平面BCD相交。
不同的视角下,线面可能“呈现”不一样的关系,因此变换视角的目的首先就是要破除可能有的图形“欺骗”效应;同时转变问题解决的思路,从概念出发反向思考,借助GeoGebra的表征优势,让MB显而易见。这样,解题过程从直观走向抽象,在图形与图形关系中抽象出数学概念之间的关系,并用数学语言予以表征。
三、联系推理,为规律论证启发思路
立体几何的学习离不开图,基本方法是“直观感知(识图)—操作确认(画图)—度量计算(算图)—思辨论证(证图)”。一方面我们需要形成一些基本模型方便识别套用(如三垂线定理);另一方面更需要形成一些问题解决观念(如空间问题转化为平面问题),将低维的问题升格到高维的视角,形成一般的方法和统一的思路。
例2:如图5,正四面体A-BCF和正四棱锥A-BCDE棱长均相等,求证:AF∥面BCDE。
这个问题其实就是1982年美国数学学会遇到的丹尼尔模型,解决这个问题的关键是将空间问题转化为平面问题。[4]考虑到O点为正四棱锥底面的中心,于是构造平面OAF(与DE、BC的交点分别为P、Q),可知△APQ、△QAF为全等的等腰三角形,则不难证明AFQP为平行四边形,这样问题便可解决。
逻辑推理是数学素养的核心,立体几何则是发展学生逻辑推理素养的重要载体。我们的教学目标并不是要建立结构完善、逻辑严密的立体几何知识体系,而是引导学生在不断深化对空间图形的认识的过程中,通过类比、转化等方法,发现和提出研究立体图形位置关系的问题,实现由表及里、从定性到定量的深化,从而学会用数学的思维思考数学问题。
四、交流分享,为自主学习创造机会
GeoGebra可以为立体几何的教学营造一个“探索数学、体验数学”的真实环境,引导学生不再仅仅向书本、向老师学习数学,更可以向技术学习数学。例如,将图5所示的情境上传至GeoGebra镜像网站,学生可在任何终端访问https://ggb123.cn/m/fw52baqx后进行实验操作(无须下载安装软件)。
事实上,教育技术融合应用下的数学课堂,可以改变传统教学中学生被动学习的状态,学生从以往的听众变成了积极的参与者,真正成为课堂的主体。学生在教师引导下进行“再创造”,使其对数学有更深刻的认识,产生更强烈的求知欲,也进一步提高了学生学习数学的积极性。
例3:从任意三角形的内切圆到任意四面体的内切球。
空间中的任意四面体可以类比平面中的任意三角形,既然任意三角形有内切圆,那么任意四面体就自然有内切球。面对学生“如何构造任意四面体的内切球”的追问,笔者并没有直接回答问题,而是启发他们运用类比的思路尝试解决。
第一,用等积法计算半径。S△ABC = S△OAB + S△OBC + S△OCA ? r = [2SAB+BC+CA] ,于是四面体中也有类似的计算,由VP-ABC =VM-ABC + VM-PAB + VM-PBC + VM-PCA ,得R = [3VS1+S2+S3+S4]。
第二,以角平分面确定球心。三角形有三条角平分线,其交点为内切圆圆心;类似的,四面体有四个(二面)角平分面,于是可猜想角平分面的交点即为内切球的球心。这样的猜想可以通过GeoGebra得到证实(先后输入下列4个指令便可完成球心M的构造):
l=平面(旋转(A,角度(平面(A,B,C),平面(P,B,C))/2,直线(B,C)),B,C);
m=平面(旋转(B,角度(平面(B,C,A),平面(P,C,A))/2,直线(C,A)),C,A);
n=平面(旋转(C,角度(平面(C,A,B),平面(P,A,B))/2,直线(A,B)),A,B);
M=交点(相交路径(m,l),相交路径(m,n))。
毫无疑问,信息技术的广泛应用正在对数学教育产生深刻影响。于是,发挥技术优势、推进新技术与教育教学的深度融合理应成为当前教育教学改革的重要课题。一方面我们需要让技术赋能,在常态化应用中创新模式,让学生经历从具体到抽象的过程,既“看到”背后的“数据”更“看透”其中的数学“内容”,而数学的眼光、数学的语言、数学的思维恰可蕴含其中;另一方面,更要发挥技术的教育价值,从具体的教学内容出发,研究学生的认知难点和技术优势,因为唯有对技术应用的创造性理解才有课堂教学的“游刃有余”。诚如《荀子》所言,“道阻且长,行则将至;行而不辍,未来可期”,我们因“心向往之”而扎根课堂,不懈前行。
【参考文献】
[1]教育部.普通高中数学课程标准(2017年版2020年修订)[S].北京:人民教育出版社,2020:27.
[2]张志勇.高中数学可视化教学:原则、途径与策略——基于GeoGebra平台[J].数学通报,2018(7):21-24,28.
[3]张景中.张景中教育数学文选[M].上海:华东师范大学出版社,2021:5.
[4]李锦昱.丹尼尔·剪拼题·空间想象能力[J].高中数学教与学,2005(5):48-49.

