Wave function collapses and 1/n energy spectrum induced by a Coulomb potential in a one-dimensional flat band system

Yi-Cai Zhang(张义财)

School of Physics and Materials Science,Guangzhou University,Guangzhou 510006,China

Keywords: wave function collapses,flat band,infinite bound states

1. Introduction

It is well known that behaviors of density of states near threshold of a continuous energy spectrum play crucial roles in formation of bound states.[37]Due to infinitely large density of density of states of a flat band,the existence conditions of bound states can be affected significantly. For example, in two-dimensional flat band system,Gorbaret al.found that an arbitrary weak Coulomb potential can destroy the flat band.[38]Furthermore,Pottelberge found that the flat band gradually becomes a continuous band (uncountable set) with the increasing Coulomb potential strength,[39]In a one-dimensional spin-1 flat band system, the bound state problem for short-ranged potential (delta potential and square well potential) has been solved by Zhang and Zhu.[40]It was found that for a square well potential of type II, the infinitely large density of states and its ensuing 1/zsingularity of Green function result in an infinite number of bound states and a hydrogen atom-like energy spectrum. Now a natural question arises: How does the long-ranged Coulomb potential of type II change the energy spectrum in one dimension? For Coulomb potential of type I,what is the energy spectrum in a one-dimensional flat band system?

In this work, we investigate the bound state problem in a one-dimensional flat band system with a long-ranged Coulomb potential. It is found that for arbitrarily weak Coulomb potential of type I, similarly to that in the twodimensional case,[38]the flat band is destroyed completely.Consequently, the flat band states evolve into the localized states which form a continuous band, which is similar to the finding by Pottelberge in two dimensions. However, we find that the localized properties of these new states in continuous band are very similar to the original flat band states. In addition, the eigen-energies of a shifted Coulomb potential depends sensitively on the cut-off parameters due to the singularity of Coulomb potential near the origin. For Coulomb potential of type II,it is interesting that the long-ranged Coulomb potential also results in an infinite number of bound states(countable set),which is similar to that of shorted-range square well potential. However, it is found that the bound state energies are inversely proportional to the natural number, i.e.,En∝1/n, which is different from its shorted ranged counterpart,e.g.,En∝1/n2in square well potential.

The article is organized as follows. In Section 2, the model Hamiltonian and the localized wave functions of the flat band are given. The localized properties are discussed with some modified Bessel functions. Next, we solve the bound state problems for Coulomb potentials of two types in Section 3. At the end,a summary is given in Section 4.

2. The model Hamiltonian with a flat band

In this work, we consider a three-component flat band Hamiltonian[40]in one dimension,i.e.,

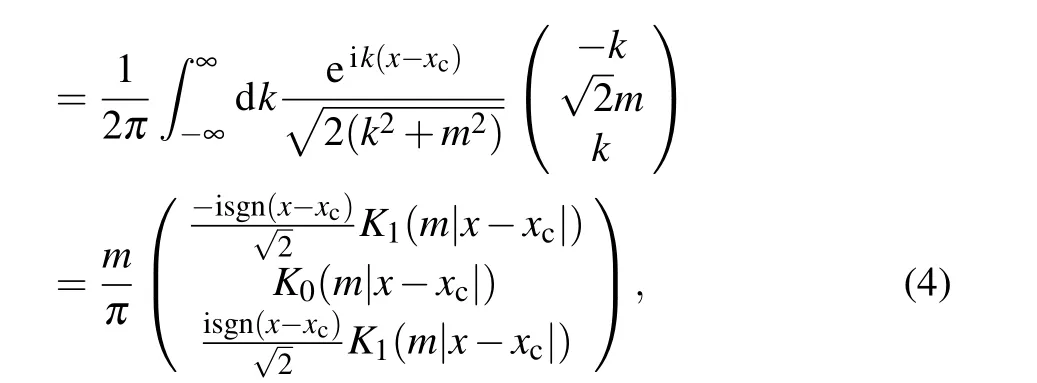
whereK0(x) andK1(x) are the zero- and first-order modified Bessel functions of the second kind,[42]respectively. The sign function sgn(x)=1 forx ＞0; sgn(x)=-1 forx ＜0 andxcdescribes the center position of the wave functionψ(x-xc)in flat band.Roughly speaking,the center position can be viewed as the particle position in the localized state(see Fig.2).

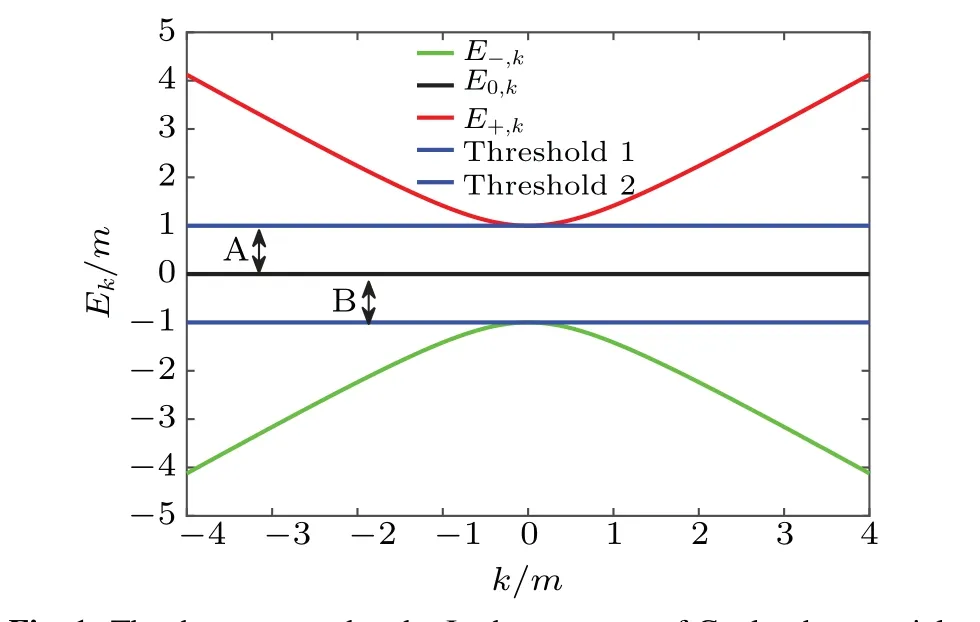
Fig.1. The three energy bands. In the presence of Coulomb potential,some bound states may exist in regions A and B.

Fig.2. Comparisons of wave functions φ2(x-xc)(un-normalized)between the trivial bound states in continuous band and the flat band states.The green,blue and red dashed lines are three flat band wave functions φ2(x-xc)for center position xc =5,10 and 15,respectively. Near the center position xc,the wave function has a logarithmic singularity,i.e.,φ2(x-xc)～-log(|x-xc|)→∞as x →xc. The green, blue and red solid lines are three corresponding wave functions for the trivial bound states in the continuous band with same center positions. The black solid line is the wave function of point indicated by black arrow of Fig.3. Here the potential strength α =0.25.

Figure 2 gives the second component wave functionsψ2(x-xc)in flat band for three differentxc=5,10,15(three dashed lines). It is shown that these flat band states are localized eigen-states,in which localized length 1/mis determined by the particle massm. Due to the logarithmic divergence of modified Bessel functionK0(x)near the originx=0,the wave function shows a logarithmic singularity near the center position,i.e.,ψ2(x-xc)～-log(|x-xc|)→∞asx →xc. In addition, in the following section, we will see that the singularity of wave function is robust even in the presence of Coulomb potential(three solid lines in Fig.2).

3. Bound states

In the following manuscript,we assume the potential energyVphas the following diagonal form in usual basis|i=1,2,3〉,namely,

3.1. Coulomb potential of type I

In this subsection,we assume that the Coulomb potential satisfiesV11(x)=V22(x)=V33(x)and

准备一杯牛奶、一大勺酸奶（最好是最新出厂的冷藏酸奶，以确保足够的活菌数）还有白糖，三者混在一起使劲搅拌，然后倒入玻璃瓶里。头一天晚上盖好盖子放到暖气上，第二天早上就能收获一大杯酸奶。整个发酵过程需要8～9 h。

whereαdescribes the Coulomb potential strength. Without loss of generality,in most of this article(except for Fig.4),we assume the potential strength to be positive,i.e.,α ＞0. Now the Schr¨odinger equation in the form of three component wave functions is

Now the non-vanishing first order derivative term would result in wave function collapses near the origin for an arbitrarily weak Coulomb potential. Consequently, the threecomponent flat band system has no well-defined bound states(near the originx=0). This is because,near the originx=0,the roots of indicial equation of the above second order differential equation[Eq.(9)]read(see Appendix A)

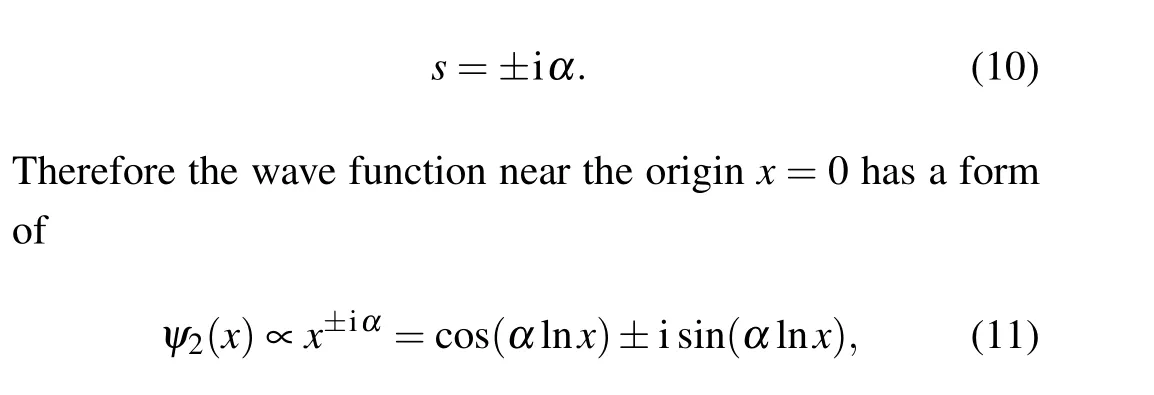
which has infinite nodes near the originx=0. It indicates that the wave function would collapse[44]for arbitrarily small Coulomb potential strengthα/=0. The Coulomb potential is too singular to have well-defined bound states in this threecomponent system. If one uses a shifted Coulomb potential,for example, 1/|x|→1/(|x|+x0) with the cut-off parameter 0＜x0≪1,[45]the bound states can exist. However, due to the wave function collapse for the true Coulomb potential,the eigen-energies would depend sensitively on the cut-off lengthx0(see Appendix A).

In order to further explore the properties of flat band states, we solve Eq. (7) numerically. The coordinate space is discretized with finite difference method. To be specific,we take the linear length of the system asL=20 and the number of spacial grids asN=2000. Therefore the spatial step Δx=L/N=0.01, and a 3N×3Nmatrix can be established with zero boundary conditions at two ends. Then we diagonalize it to get the eigen-energies and eigen-states. The results are reported in Figs.2 and 3.

It is found that once the Coulomb potential is turned on,the flat band gradually evolves into a continuous band (see the blue lines in Fig. 3), and then the flat band is destroyed completely by an arbitrarily weak Coulomb potential,which is similar to two-dimensional result.[38,39]At the same time,the original flat band states have been transformed into the states of the continuous band.

We plot the wave functions for three typical states in the continuous band(solid lines in Fig.2).It is found that the wave functions of these states are also localized with three center positionsxc=5,10,15,respectively.These localized states basically inherit the localized properties of original flat band states(see the dashed lines of Fig. 2), for example, the logarithmic singularity near thexc.This is because for the Coulomb potential of type I, the three diagonal matrix elements of potential are equal(in the usual basis)[see Eq.(6)]. One can also view the potential energy in the energy band basis(|+,k〉,|0,k〉and|-,k〉), consequently the diagonal form with three equal matrix elements is also unchanged approximately. Therefore for the three energy bands(flat band,upper and lower bands),they experience three same Coulomb potentials.

Due to the spatial localization of the flat band states,once the potential is turned on,the energies of these localized states atxonly shift a value ofV(x),i.e.,E=0→E=0+V(x)=α/x.Consequently,the localized properties are basically same to the original flat band states. Therefore, in this sense, we call them the“trivial bound states”. It should be remarked that these bound sates (localized atxc=α/E) are far away from the originx=0, then the wave functions are not affected by the wave function collapses near the origin.

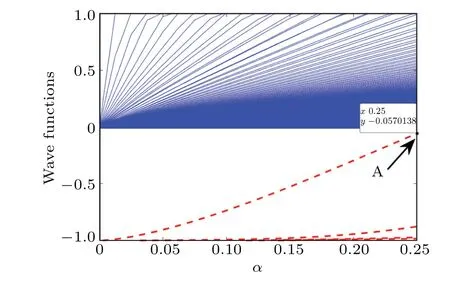
Fig. 3. The bound state energy of Coulomb potential of type I. The bound state energies are obtained with finite difference method. The flat band gradually becomes a continuous band (the blue solid lines).The red dashed lines are the bound states near the origin for the shifted Coulomb potential 1/(|x|+x0).

In addition, for positive (negative) potential strengthα,some states in lower(upper)band can be pushed(pulled)into the gaps,and then they form bound states(see the red dashed lines in Fig. 3). We should point out that these bound states are not true bound states for a true Coulomb potential with 1/xsingularity. These bound states are due to our finite difference method. In our numerical method, the spatial step Δxis always finite,so we could not faithfully simulate the true 1/|x|singularity of Coulomb potential near the originx=0. In fact,the true Coulomb potential would result in the wave function collapses. Consequently, any well-defined bound states near the originx=0 could not exist. Due to the finiteness of spatial step Δx,the 1/|x|singularity near the origin has been shifted,e.g., 1/|x|→1/(|x|+x0) with the cut-off parameterx0≪1.Then,the bound states can exist in the shifted Coulomb potential. Due to collapse nature of wave function near origin, the eigen-energy depends sensitively on the cut-off lengthx0(see Appendix). The wave function [ψ2(x)] for a typical bound state (corresponding to the point in Fig. 3 indicated by black arrow) in the shifted potential is reported in Fig. 2 (see the black solid line). In comparison with the trivial bound states,the wave function of the bound state near the origin has no logarithmic singularity.

3.2. Coulomb potential of type II

In this subsection, we assume the potential energy satisfiesV11(x)=V33(x)≡0 and

It is found that there exist infinite bound states generated from the flat band. For a givenn, whenα →∞, the energy approaches the thresholds of continuous spectrum, i.e.,En →±m,which is similar to that of short-ranged potential.[40]The wave function(see Fig.5)

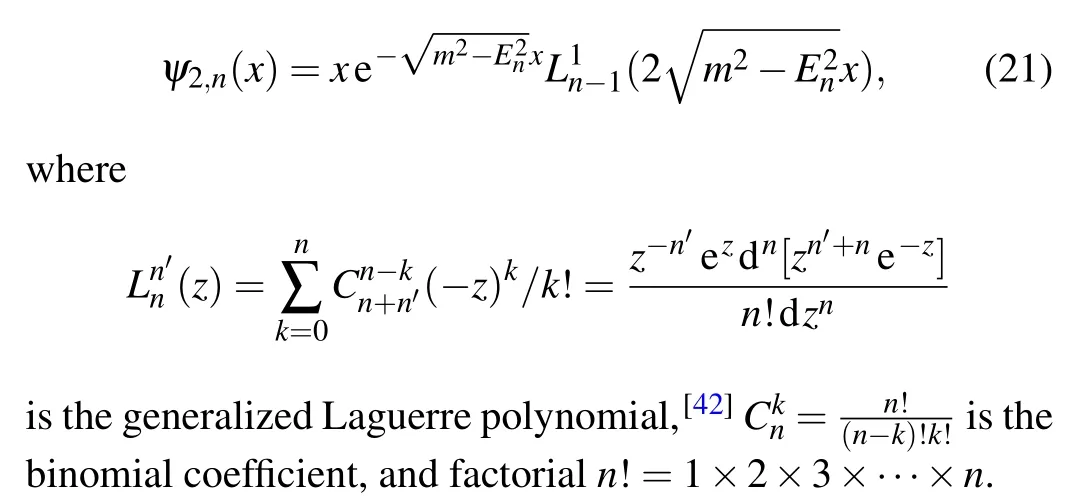
Fig. 4. The bound state energy of Coulomb potential of type II[Eq.(21)].

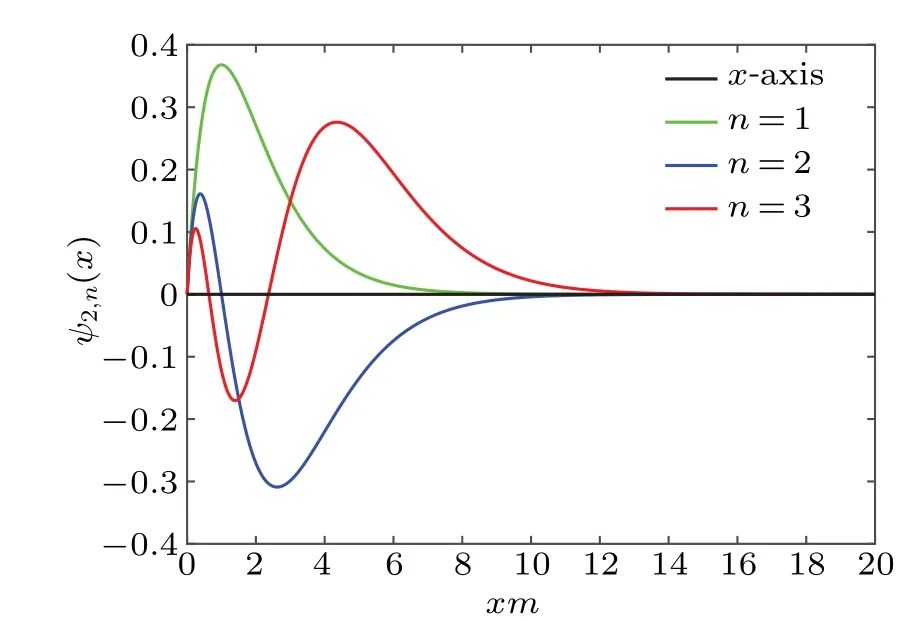
Fig. 5. The three (un-normalized) wave functions of Coulomb potential potential of type II[see Eq.(21)],with quantum number n=1,2,3.Here the potential strength α =0.25.

Whenα ≪n,the energy can be approximated with

where quantum numbern=1,2,3,.... For everyn, due to the presence of parity symmetry(x →-x),the eigen-energy is doubly degenerate, which corresponds two eigen-states with an odd parity and and an even parity. When the potential strengthαis small, the eigen-energy is proportional toα,which is similar to the short-ranged potential case.[40]In addition,it shows that,in the presence of long-ranged Coulomb potential, the bound state energy is inversely proportional to the natural number,i.e.,En∝1/n,which is different from that(En∝1/n2)in the case of short-ranged square well potential.En∝1/nof the Coulomb potential makes level distances between the adjacent states apart farther than that 1/n2of shortranged square well. It indicates that the long-ranged potential has more abilities to pull some states out the flat band than its short-ranged counterpart.

4. Conclusion

In summary, we have investigated the bound states in a spin-1 Dirac model with a long-ranged Coulomb potential. It is found in the presence of Coulomb potential of type I, the flat band is destroyed completely. Furthermore, the flat band evolves into a continuous band with the increasing of potential strength. The states in the continuous band have a similar logarithmic singularity as that of the flat band states. In addition,the Coulomb potential causes the wave function collapses near the origin. Due to collapses near the origin,the eigen-energies of shifted Coulomb potential depend sensitively on the cut-off length.

In the presence of Coulomb potential of type II,there exists an infinite number of bound states, which is generated from the flat band. Furthermore, when the bound state energies are near the zero energy of the flat band, the energies are inversely proportional to the natural number, e.g.,En∝1/n, which is different from that of its shorted-ranged counterpart, i.e.,En∝1/n2in square well potential. It is expected that the wave function collapses and 1/nenergy spectrum could be verified experimentally[46–49]in future. Finally,the Coulomb potential of type III would also result in the 1/nenergy spectrum,[50]and bound state in the continuous spectrum(BIC).[51]

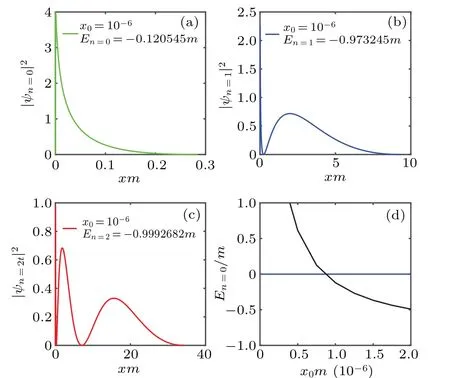
Fig. A1. The squares of (un-normalized) wave functions and eigenenergy for a shifted Coulomb potential α/(|x|+x0). The panel(a),(b)and(c)are the squares of three wave functions with x0=10-6,and the Coulomb potential strength α =0.25. The panel(d)shows the increasing eigen-energy E0 with the decreasing x0. Here the quantum number n is the number of nodes of wave function (except for two ends of interval,x0 and x1). The quantum number for the“ground state”is n=0.Due to the potential strength α ＞0 (repulsive potential), the ground state ψ0 has highest energy among these bound states.

The results are reported in Fig.A1. The panel(d)shows that the ground state energyE0grows up with the decreasing cut-off parameterx0. Due to the wave function collapses near the originx=0,the eigen-energies depend sensitively on the cut-offx0. In addition, the weights of wave functions accumulate gradually near the origin. This reflect that the wave function collapses,and the system has no ground state for true Coulomb potential.

Acknowledgements

We acknowledge the supports of startup grant from Guangzhou University. This work was supported by the National Natural Science Foundation of China (Grant No.11874127).