内角和定理的分层练习教学法初探

山东滨州实验学校（256600）张淑华

“自己有一桶水，才能给学生一瓢水。”教师必须知识渊博，见识不凡，同时具备优秀的教学设计能力，只有这样才能在教学中高屋建瓴，从大局出发，从细微处着眼，将精细的知识点合理巧妙地融合成知识体系，才能科学恰当地拓展学生思维，做到点到即止，恰到好处。为了提高三角形内角和专项练习的效率，笔者主要采取分层练习教学法，将单一的练习题做了延伸，使其覆盖面更广。现将试教的成果整理如下，供各位同行参考。

一、基础练习热身

练习1.请判断下面哪组的三个角能组成一个三角形。

①70°、60°、50° ②65°、65°、50°

③37°、53°、100° ④90°、40°、50°

（学生仔细分析研判每组角的度数，发现①②④三组角的和均为180°，判定它们可以组成三角形。与此同时，进一步仔细观察后发现，②组组成的三角形实为一个等腰三角形，而④组组成的三角形则是一个直角三角形。）

师（追问）：能画出④组数据所表示的三角形吗？（学生画图）

师（挑出两个大小不一的直角三角形投影到电子白板上）：为什么大小不一呢？

生1：因为边长可以灵活伸缩。

师：换言之，三角形的三个角永恒不变时，什么可以千差万别？

生2：面积大小以及各边的长。

（教师利用投影仪，将两个三角形的最小内角（40°）叠放在一起，然后沿水平方向平移较大三角形的直角边，与另一个三角形的非平行边相交形成一系列的组合直角三角形（如图1）。）

图1

师：仔细观察这些组合而成的直角三角形，哪些元素发生了变化？哪些元素维持原样？

生3：三角形的大小在变，但是三角形的三个内角没变。

练习2.推算图2中各个三角形中∠B的大小。

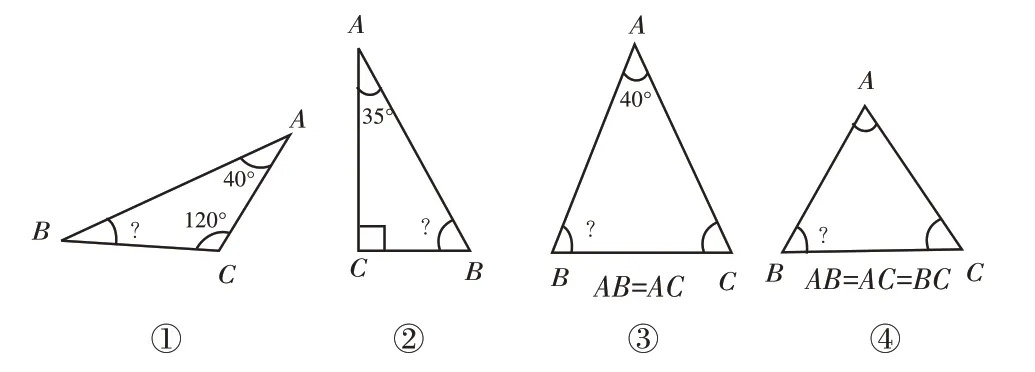
图2

（学生独自列式计算后，教师组织交流活动，并点拨学生根据②③④这三幅图的形体特征归纳便捷算法。）

【评析】通过运用“三角形内角和”定理推算内角，让学生迅速回顾旧知。值得肯定的是，教师让学生依据直角三角形的三个内角大小画出三角形图案，这貌似一个不起眼的画图举动，实际上隐喻了“相似三角形”的概念。学生在画图、对比、反思中发现，虽然三个内角始终恒定，但是边长却可以任意伸缩。通过投影显现三角形的三条边伸缩比例是同频同步同比的，这也隐含了相似三角形对应边成比例的定理。之后推算内角度数的练习，及时巩固了内角和定理，稍带回顾了特殊三角形的内角分布等知识。

二、拓展练习训练

1.利用内角和定理推算外角

电子白板显示一：内外有别，用三角形内角和定理可以推算它的外角，这叫内外兼修。

师（出示图3）：图3中的∠1、∠2、∠3都是延长三角形一边所得，称为三角形的外角。请同学们按要求答题。①分别推算出每个三角形中指定角的大小。②观察分析运算结果和所有角的度数，看看有没有什么规律可循。

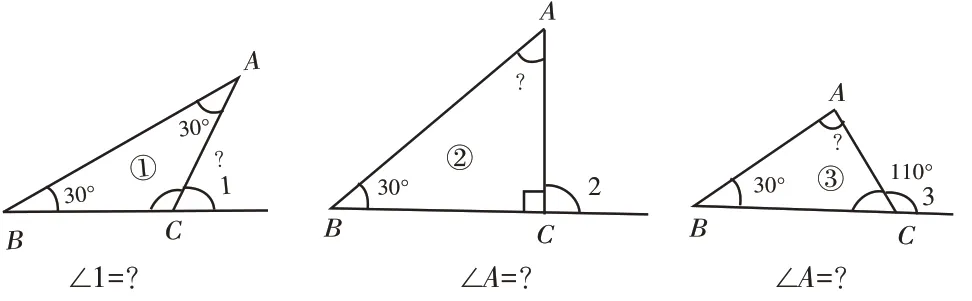
图3

（学生独自思索、演算，组内磋商，再交流反馈）

板书：图形①，先计算∠1的邻补角，180°-30°-30°=120°，再从平角中剪切得∠1=180°-120°=60°。图形②直观反映出∠2为直角，因此它的邻角应该是直角的补角90°，于是根据内角和定理推知∠A=90°-30°=60°。图形③，先根据外角求出内角∠C的度数，180°-110°=70°，再运用内角和定理求值，∠A=180°-30°-70°=80°。

生：三角形的外角正好等于不相邻的两个内角之和。

师：有根据吗？敢肯定吗？

（学生复核后确认。教师用光标点击图形①的C点，使其变成动点（A、B仍为定点），并沿着BC所在直线向右平移，使学生亲眼看见外角∠1由小到大的动态变化过程，而不相邻的内角∠A也会随之变化。）

【评析】教师引进外角的真实用意是让学生通过观察、利用外角与邻近内角的互补性以及对三角形内角分配的影响，掌握内角和定理。学生从中发现三角形的外角等于不相邻的两内角之和，这是自主探究的收获。让学生经历观察发现规律的过程，有效历练了学生的自主探究能力。

2.利用三角形内角和研究多边形的内角和

师：三角形内角和不但可以解决外角的问题，还能解决多边形的内角和问题。

电子白板显示二：运用三角形内角和来推导多边形的内角和定理。

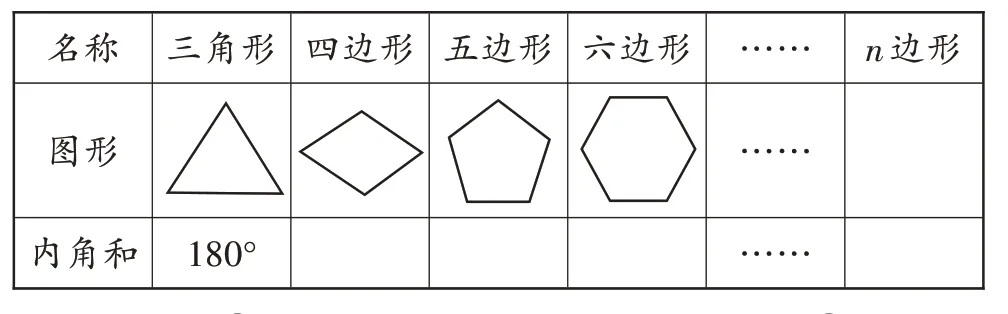
名称图形内角和三角形180°四边形 五边形 六边形 ………………n边形

要求：①观察表中各图有几个内角；②请你想办法求出各图的内角和；③寻找规律，探讨计算公式；④组内交流。

生：四边形沿着一条对角线可分割成两个三角形，因而它的内角和是2×180°=360°；从五边形的一个顶点出发，沿着2条对角线可将其分割成三个三角形，因此它的内角和是3×180°=540°；从六边形的一个顶点出发，沿着三条对角线可将其分割成四个三角形，因此它的内角和是4×180°=720°……

师（在表中的图上演示对角线连接法）：按规则把图形分成几个三角形后再计算，你们从中发现了什么规律？

（学生对比归纳类推，概括出“n边形”的内角和公式——（n-2）×180°。教师呈现“凹凸”两种多边形，以四边形和五边形为例（如图4）。）

图4

师：它们的内角和是否还能沿用上述公式？

（教师用图示法，使学生领悟这里的凹多边形仍然可以沿用上述公式求内角和（如图5），只是分割时要从凹点引线。）

图5

师：这个公式是否对任意凹多边形都管用？（暗示学生课后继续研究）

【评析】设计多边形内角和问题，用意是让学生通过观察、尝试、计算、分析，发现共性，提炼公式，丰富学生的数学操作活动经验。归纳凸多边形的内角和公式难度不大，但教师并没有止步于此，触角继续延伸到凹多边形，引导学生探究发现提炼出的公式“凹凸”通用，唯一不同的是，将凹多边形切分成三角形时，必须从凹点引线。教师用一个问题“这个公式是否对任意凹多边形都管用？”将研究范围延伸至课外。

三、由静到动，深化理解

1.研究顶角的变化

师：任意三角形的内角和始终是180°。图6是一个直角三角形。

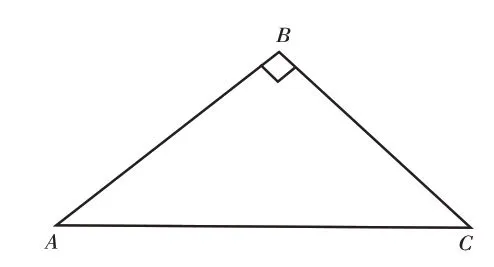
图6

师：现将顶点沿着高线上下平移，先后形成三角形AB1C和三角形AB2C（如图7）。

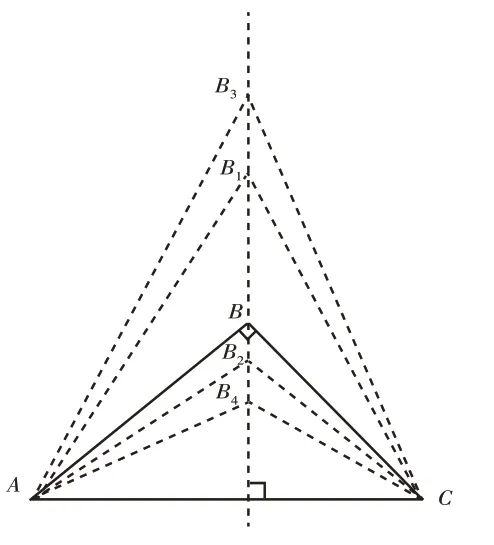
图7

师：观察三角形AB1C和三角形AB2C，它们的内角较之前有什么变动？平移顶点后形成的两个三角形是什么三角形？

（学生独自思索，合作探讨后汇报展示。）

生1：三角形AB1C的顶角缩小，底角变大。原图演变成锐角三角形。

生2：三角形AB2C的顶角变大，底角缩小。原图演变成钝角三角形。

师：发挥想象，若继续加大平移幅度，原三角形的顶角和底角会呈现什么变化趋势？

生：顶点越往上移动，顶角越小；顶点越往下移动，顶角越大。

2.研究与圆有关的三角形内角的变化

师：刚才顶点是沿着高竖直移动，假如沿着圆弧移动，会是怎样呢？

师（先投影一个圆，再画直径AB，在圆弧上任意取点C，并连接CA、CB，组成一个三角形，如图8）：这样内接在圆内的三角形会是什么形状？

图8

（学生不断画图试验，发现所画的三角形均为直角三角形。）

师：在圆弧上随意定点C，连接CA、CB，得出的三角形ABC仍是直角三角形吗？

（学生探究核查）

师：对比这些直角三角形，直角对应一条半圆弧，另外两个锐角对应的弧线合起来也是一条半圆弧，因为这两个锐角的和也是90°。

师：在圆外随意取点，再来连接三角形。此时的三角形又是什么形状？是什么三角形？

（学生操作探究，发现所得的三角形都是锐角三角形，如图9。）

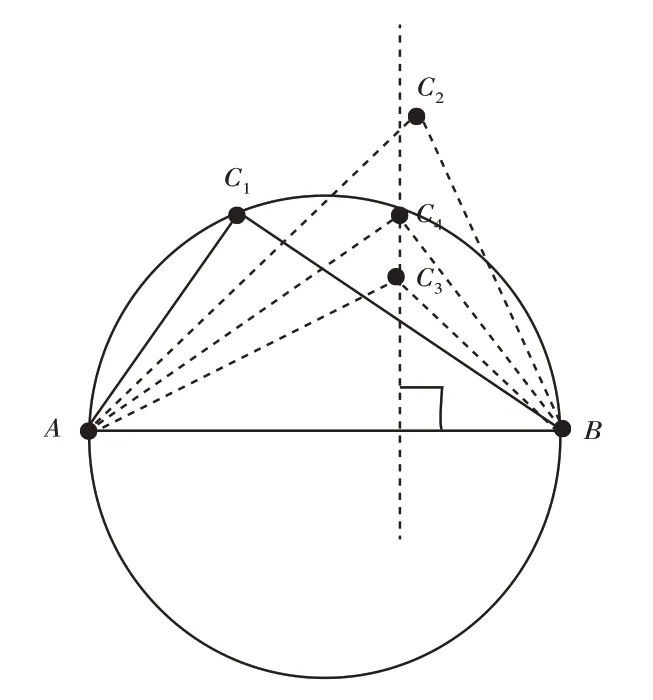
图9

师：请大家再在圆内取点，所得的三角形会是什么形状？

（学生又经过反复操作探究，发现其形状是钝角三角形，如图9。此时学生无比兴奋。）

师：过一个钝角三角形的钝角顶点，到对边画出垂线，与圆弧相交于C点，这一点与A、B连接成的是一个直角三角形。

师：通过刚才的操作，你明白其中原委吗？

【评析】在“图形与几何”教学中做到化静为动颇费功力。一般在展示动图之前，应先让学生对静态图形进行观察和想象，再来演示，这样就能使演示的图形与学生的设想形成对应。教师先让学生观察探究三个静态的三角形，再动态演示顶点上下平移，让学生直观感知顶角变化带来底角变化的过程，然后让学生想象加大平移幅度后的情景，为研究圆与三角形的相关知识进行了预热。