基于相邻单元高斯点方案的应力恢复方法

卿光辉，徐靖峪

（中国民航大学航空工程学院，天津 300300）

通常情况下，位移有限元法的节点位移精度高[1]，但由于导数运算后应变插值函数的阶次降低，导致应力结果精度低于位移结果精度。为了提高位移有限元法的节点应力精度，Oden 等[2]提出了将相邻单元在公共节点处的应力取平均值来获取改进的应力结果，但这种方法所得到的应力结果误差较大。Hinton 等[3]基于最小二乘法思想提出了总体应力磨平法，但该方法的计算量大，一般不被人们所采用。单元应力磨平法[3-4]可以方便地利用精度较高的高斯点（最佳应力点）的应力值，提高节点上的应力结果精度，将高斯点应力用节点应力改进值构造的插值函数表示，然后4 个节点的应力可由高斯点的应力外推得到，最后可将相邻单元在公共节点的不同数值结果取平均值作为该节点的应力结果[5]。 该方法也称为外推法，是目前最常用的一种应力恢复方法。外推法具有普遍适用性，但主要缺点是节点上的应力值是通过外推法得到的，未能充分利用单元最佳应力点精度高的特性，在应力梯度较大处或非均匀网格模型中，这种方法具有一定的局限性[6]。 文献[5]也指出外推法所获得的节点应力精度相对于高斯点上的应力而言并不十分理想。 文献[7-9]提出的分片应力磨平法和改进的平衡分片磨平法能较大幅度地提高节点的应力结果精度，但由于该方法较为复杂，且对规则的正交有限元网格无效，因此，包含这类应力恢复法的商用软件并不多见。Zhang 等[10]提出了一种对节点位移进行最小二乘拟合的应力恢复方法，可提高应力结果精度；徐小明等[11]结合辛对偶体系下的解析辛本征展开解，提出了一种关于二维问题的应力磨平方法，使得特定域内应力场具有与位移场相媲美的精度，但对于不同的问题，该方法中的应力解析函数不确定。

随着近年来研究的不断深入，一些新的应力恢复技术被提出。 Sharma 等[12]提出了一种低阶有限元应力恢复技术，通过平衡条件得到改进的恢复应力场；Moslemi 等[13]提出了一种基于每个高斯点应力值分布统计的误差估计方法，获得了有利于应力计算的最优有限元网格；赵亚飞等[6]应用高斯过程回归方法对有限元应力解进行了改善研究。

随着人工神经网络被广泛应用于有限元方法进行结构分析，Khoei 等[14]提出了一种采用前馈-反向传播多层感知器（MLP，multi layer perceptron）神经网络的应力恢复技术来提高节点处应力场的精度。该方法基于后验Zienkiewicz-Zhu 误差估计，实现了自动自适应网格细化， 适用于高应力梯度区域的应力场恢复，在应力奇异性问题上也能有效地改善应力场。

综上，针对二维非协调4 节点四边形单元模型，提出一种基于相邻单元高斯点应力精度高的特性应力恢复方法，并通过数值算例验证该方法的精度和有效性。

1 基础理论

1.1 4 节点四边形单元的非协调形函数

根据非协调位移元理论[15]，4 节点四边形单元的位移场u=[u1u2]T和应力场σ=[σxσyσxy]T可表示为

式中：N 是单元形函数矩阵；Nλ是内部点位移形函数矩阵；qe是单元节点位移列阵；λe是单元内部点位移列阵；pe是单元节点应力列阵。

1.2 二维问题非协调位移元列式

最小势能原理的表达式[16]为

式中：Δ为微分算子矩阵；C 为材料弹性矩阵；V 为结构体积；b 为物体所受的体积力；Sσ为结构表面积；为作用在结构表面积Sσ上的已知应力。

将式（1）代入式（3），得到离散形式最小势能原理表达式为

忽略内部节点力fλ[15]，式（4）分别对节点位移qe和内部节点位移λe变分，得到

由式（6），可将λe用qe表示为

将式（7）代入式（5）消去λe，得到非协调位移元的基本方程

2 基于相邻单元高斯点的应力恢复

2.1 单元高斯点的应力计算

位移有限元法的变量精度问题可归结为求解如下泛函

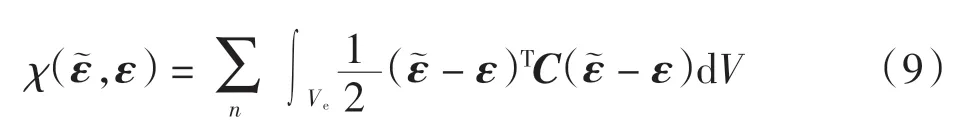
的极小值[3，17]，即求解

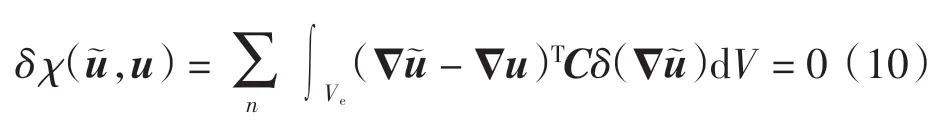
值得说明的是，以上理论的前提是单元的雅可比行列式是常数，且每个应力分量是独立假设的，所以该理论只适应于一维单元。 但对于二维四边形线性单元或三维六面体单元，实用结论是：在等参元中n+1阶高斯点上的应变或应力近似解比其他部位具有较高的精度，这些点习惯上被称为最佳应力点。 因此，通常情况下，一般首先利用本构关系求出单元具有高精度的高斯点应力，然后以高斯点应力值为基础再设法求节点的应力。

对于一般的等参元，由本构关系可得到单元精度较高的高斯点应力

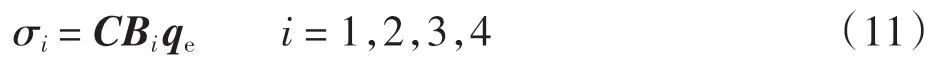
式中：Bi为代入每个高斯点自然坐标后的应变矩阵；qe为该单元节点位移列阵。 由式（11）可得到待求应力节点所有相邻单元的高斯点应力，在此基础上，可充分利用这些高斯点的应力，通过插值方法得到待求节点应力，该方法可称为相邻单元法。对于模型中不同位置的节点，可采取不同的插值方案。

2.2 内部节点的应力恢复

当待求节点为模型的内部节点时，围绕待求应力的内部节点的高斯点构造等参单元，然后应用内推法计算包含在此单元内部的节点应力。

图1 中，k 为一个内部节点， 是单元A、B、C、D 的公共节点，这4 个单元为节点k 的相邻单元，其中每个单元内都有Ⅰ、Ⅱ、Ⅲ、Ⅳ4 个高斯点。 从相邻单元的高斯点中选取距节点k 最近的4 个高斯点， 且这4个高斯点需要构成一个凸四边形。 这样，这4 个高斯点可构造出一个包围节点k 的四边形单元，如图1 中虚线所示，4 个高斯点是此单元的4 个节点。

图1 内推法新单元的构造方式Fig.1 The construction of the new unit of interpolation method

视新单元为等参元，令4 个高斯点的自然坐标：A（Ⅲ）为（-1，1），B（Ⅰ）为（1，1），C（Ⅳ）为（-1，-1），D（Ⅱ）为（1，-1），新单元中任意一点的总坐标可由等参元坐标公式给出

式中：（xi，yi）是高斯点i 的总坐标；Ni为高斯点i 对应的插值函数，（1+ξiξ）（1+ηiη），ξi和ηi表示高斯点i 的自然坐标（ξi，ηi）。

设（ξ，η）是节点k 的自然坐标，由于ξ 和η 均在（-1，1）区间内，则由式（12）可求出节点k 在新单元中的自然坐标。 图2 表示了等参元自然坐标系下节点k与4 个高斯点的位置关系。

图2 等参变换后的新单元Fig.2 The new unit after isoparametric transfer

基于等参元理论，单元内任意一点的应力可由4个节点的应力表示

将通过式（12）求得的节点k 的自然坐标代入式（13）中，即可得到节点k 的应力结果。 显然，相邻单元法避免了常规的外推法中相邻单元在公共节点处应力结果取平均值的过程，计算程序更加简便。

2.3 边界节点的应力计算

图3 所示，边界节点与最近的内部节点之间也分布着单元内的高斯点。如果采用线性拉格朗日插值法[19]求边界节点应力，则需要取两处已知的具有高精度应力值的点来构造线性插值函数向外插值出边界节点的应力。图3 中：c 点是距离待求边界节点a 最近的内部节点，假设内部节点c 已采用2.2 节的方法求得了应力值；b 点是内部节点和边界节点边线上的中点，该点应力的求解方法与2.2 节中内部节点应力的求解方法相同。

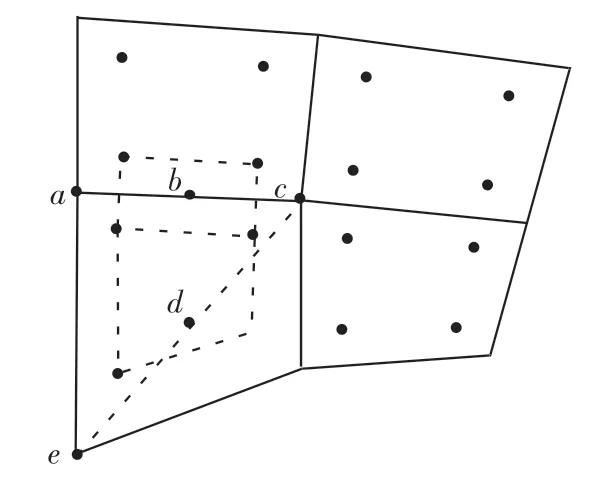
图3 外推边界节点应力过程Fig.3 Process of extrapolating the stress

图4 中，以σb表示中点b 的应力，横坐标取1，以σc表示内部节点c 的应力，横坐标取2，构造插值多项式，则满足

图4 外推法的插值函数Fig.4 Extrapolation function at external nodal

y=L（x）的几何意义即通过两点（1，σb）和（2，σc）的直线，L（x）的表达式为

由边界节点a、中点b 和内部节点c 的关系可知，L（0）即为所求边界节点a 的应力值。

若待求的边界节点是角节点（如图3 中的点e），同理，选取内部节点c、两点连线的中点d，应用2.2 节中的方法可以计算包围点d 的应力，再由式（15）可给出角节点e 的应力值。

值得说明的是，在使用相邻单元法进行应力计算时：一方面，虽然边界节点采用了外插法，但从理论上讲，对于线性插值方法，内部节点和外部节点的插值结果精度相同；另一方面，在实际问题中，不同应力分量沿不同方向的变化规律不同，且在非正交网格中构造插值函数时，边界节点、中点和内部节点连线方向具有任意性，且应力可能并不呈线性变化，但若边界的网格划分较密，线性插值法得到的应力值，通常不会出现较大误差[20]。

3 数值算例及分析

3.1 经典梁问题

算例1考虑平面应力状态下简支矩形梁（如图5所示）。 几何参数：梁的半宽c=1，梁的长度L=10，厚度t=1。材料参数：弹性模量E=1 000，泊松比v=0.25。载荷P=80，位移边界条件为：u1（L，0）=u2（L，0）=0，u1（L，c）=u2（L，-c）=0，应力边界条件[21]为：在x=0，-c ≤y ≤c 处

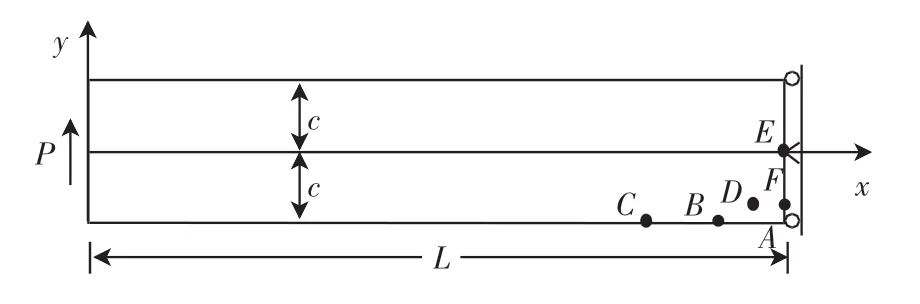
图5 简支矩形梁算例示意图Fig.5 Diagram of a simply supported rectangular beam

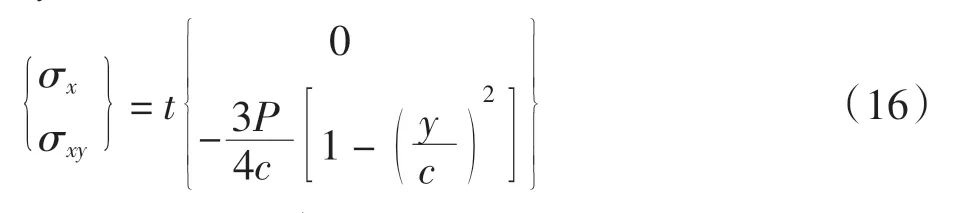
在x=L，-c≤y≤c 处

算例2考虑平面应力状态下一端固支的矩形梁（如图6 所示）。几何参数：梁的半宽c = 1，梁的长度L =10，厚度t=1。 材料参数：弹性模量E=1 000，泊松比v = 0.25。载荷P = 100，位移边界条件为：x = L，-c≤y≤c 时，u1=u2=0，应力边界条件[22]为：在x=0，-c ≤y ≤c 处

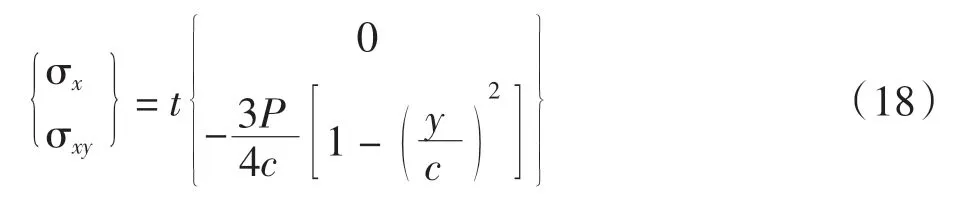
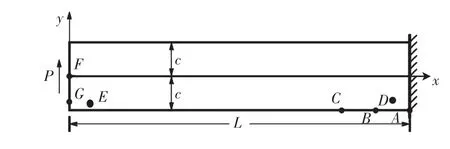
图6 一端固支的矩形梁算例示意图Fig.6 Diagram of rectangular beam fixed at one end

两个算例的有限元网格模型如图7 所示。 表1 和表2 分别列出了两个算例中的点A（x=L，y=-c），点B（x=0.9L，y=-c），点C（x=0.8L，y=-c）和点D（x=0.95L，y=-0.75c）的应力σx的值。表3 和表4 列出了算例1 中的点D（x = 0.95L，y = -0.75c），点E（x = L，y =0），点F（x=L，y=-0.75c）和算例2 中的点E（x=0.05L，y=-0.75c），点F（x=0，y=0），点G（x=0，y=-0.75c）的应力σxy的值。 算例1 精确解参见文献[21]，算例2精确解参见文献[22]。 两个算例中σy的精确解全域为0，故在此σy的计算结果不作对比。误差率计算公式为

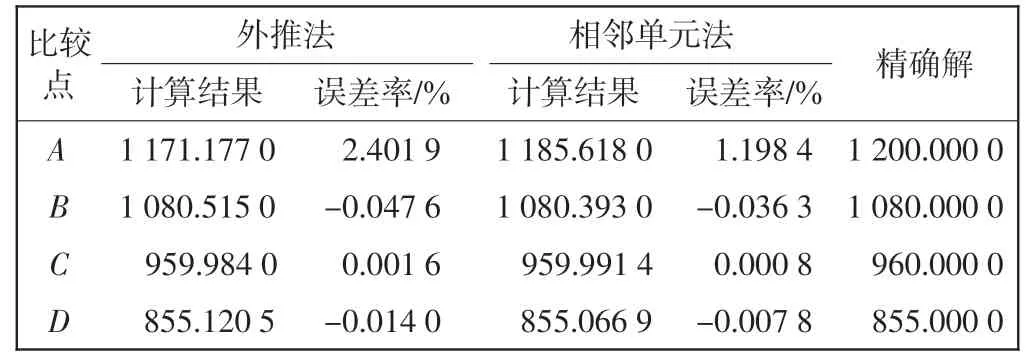
表1 网格模型1 A、B、C 和D 点的应力σx（算例1）Tab.1 Stress σx at points A，B，C and D（Case 1）of mesh 1

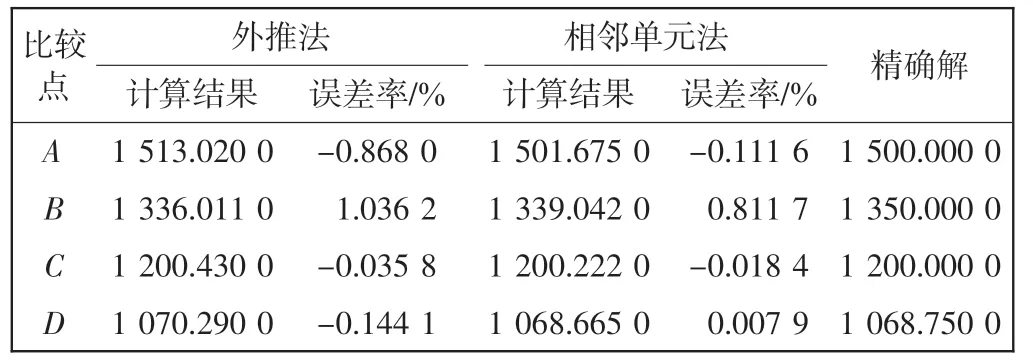
表2 网格模型1 A、B、C 和D 点的应力σx（算例2）Tab.2 Stress σx at points A，B，C and D（Case 2）of mesh 1

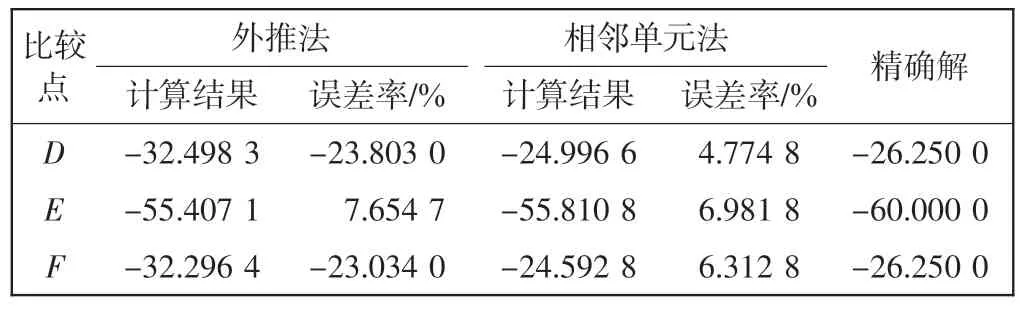
表3 网格模型1 D、E 和F 点的应力σxy（算例1）Tab.3 Stress σxy at points D，E and F（Case 1）of mesh 1

图7 网格模型1：20×4 正交四边形网格Fig.7 Mesh 1：20×4 orthogonal quadrilateral mesh

式中：σexact为应力精确解；σdata为应力有限元解。

从表1～表4 中可看出，相邻单元法的应力和结果精确度比外推法的结果精确度明显提高。

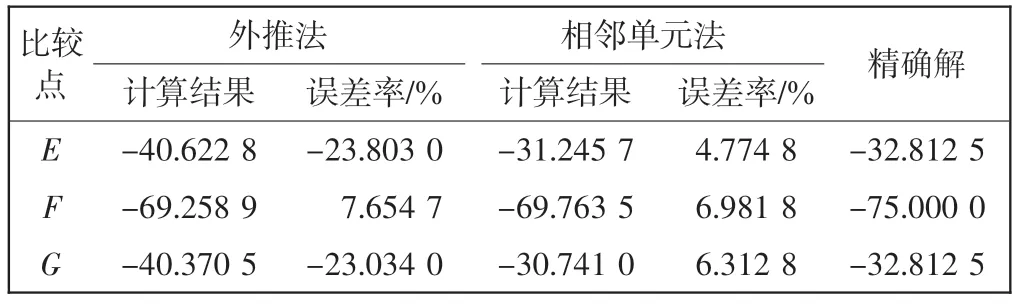
表4 网格模型1 E、F 和G 点的应力σxy（算例2）Tab.4 Stress σxy at points E，F and G（Case 2）of mesh 1

采用图8 所示的非正交网格模型时计算结果如表5～表8 所示。

图8 网格模型2：非正交四边形网格（157 单元）Fig.8 Mesh 2：non-orthogonal quadrilateral mesh（157 elements）

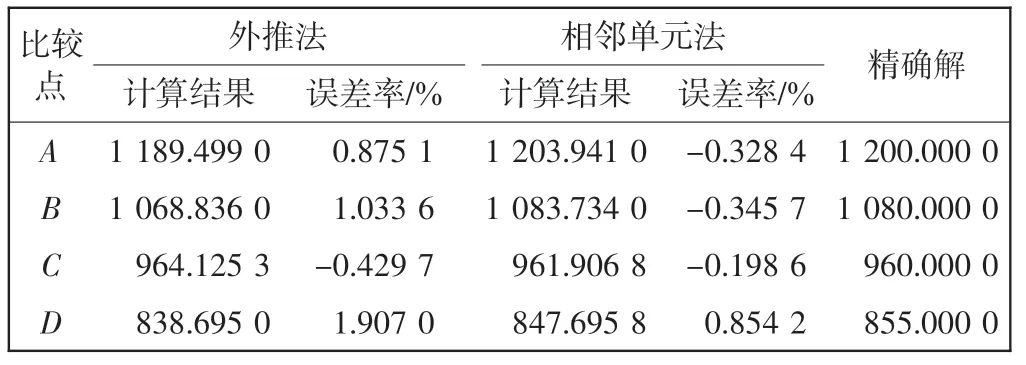
表5 网格模型2 A、B、C 和D 点的应力σx（算例1）Tab.5 Stress σx at points A，B，C and D（Case 2）of mesh 2

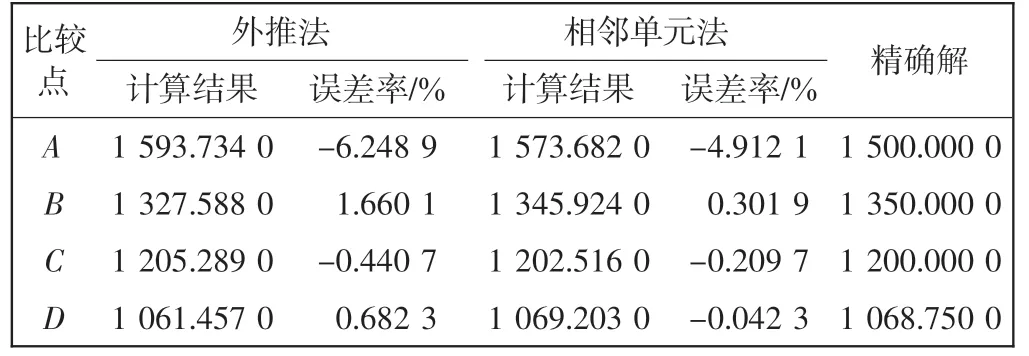
表6 网格模型2 A、B、C 和D 点的应力σx（算例2）Tab.6 Stress σx at points A，B，C and D（Case 2）of mesh 2

表7 网格模型2 D、E 和F 点的应力σxy（算例1）Tab.7 Stress σxy at points D，E and F（Case 1）of mesh 2

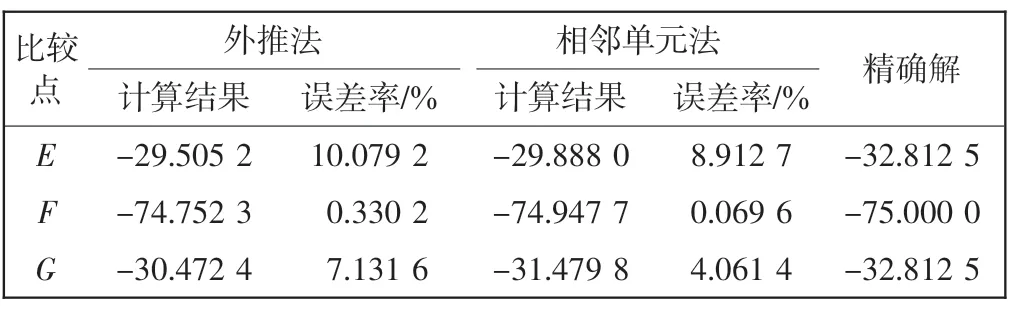
表8 网格模型2 E、F 和G 点的应力σxy（算例2）Tab.8 Stress σxy at points E，F and G（Case 2）of mesh 2

从表5～表8 中可以看出，对于不均匀的非正交网格模型，相邻单元法的结果精确度也优于外推法。

3.2 收敛性分析

考虑算例1，5 种均匀的正交网格模型分别为10×2，20×4，30×6，40×8，50×10。 图9 和图10 分别列出了5 种网格模型边界上的应力σx（L，-c）与σxy（L，0）的收敛情况，横坐标为单元x 方向尺寸的对数，纵坐标为误差率error。 图9 和图10 表明，相邻单元法在计算应力σx和σxy时均满足收敛要求，且在相同密度的网格下计算结果误差率要小于常规的外推法。

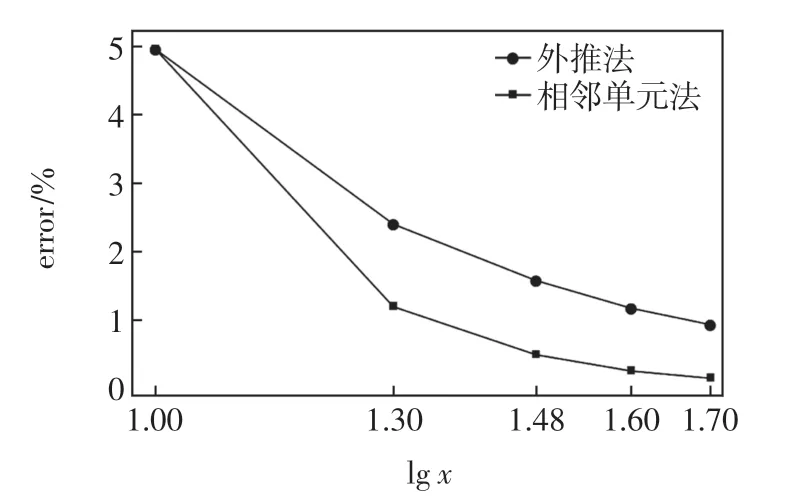
图9 σx（L，-c）收敛性Fig.9 Convergence of σx（L，-c）

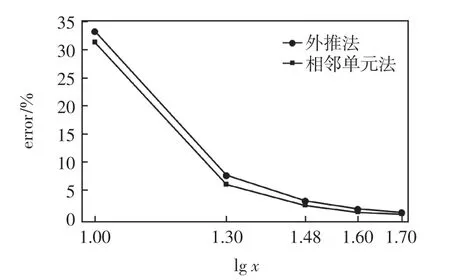
图10 σxy（L，0）收敛性Fig.10 Convergence of σxy（L，0）

3.3 板中含孔应力集中问题分析

算例3考虑如图11 所示中心含圆孔的方形板。板长、宽均为a=8；孔半径r=1；厚度t=1。材料参数：E=1 000，v=0.25。如图12 所示，采用其1/4 模型划分网格并进行分析，位移边界条件为：x=0 处，u1=0；y=0 处，u2=0；x=4 处，受均布载荷q=1。

图11 含圆孔的方形平板几何参数Fig.11 Geometric parameters of square plate with circular hole

图12 算例3 网格模型与受载情况Fig.12 Mesh and loads of case 3

为研究模型应力集中位置的应力结果精确度，表9 列出了点A（0，1）处的应力σx和点B（1，0）处的应力σy的有限元解和精确解[22]及误差率。 从表9 中可以看出，相邻单元法在计算应力集中位置的应力结果精确度优于常规的外推法。

表9 应力集中位置σx 和σy（算例3）Tab.9 Stress σx and σy at position of stress concentration（Case 3）

4 结语

基于位移结果得到的单元高斯点的高精度应力，提出了一种新的应力恢复方法。 具体结论有：计算内部节点应力的内推法避免了外推法中相邻单元在公共节点的应力结果取平均值的计算过程，计算边界节点应力采用线性插值方法，计算较为简便。 数值算例表明，在相同的网格模型情况下，所提出的相邻单元法比常规的外推法应力计算结果精确度高，该方法对正交网格与非正交网格均适用。 为了进一步验证方法的正确性，对边界上应力结果的收敛性情况进行了分析，应力结果满足收敛性要求且相较于外推法精度更高。在对含圆孔方形板应力集中问题的分析中，运用该方法计算所得的应力集中系数比外推法更接近理论解，可更有效地预测由应力集中现象引起的含孔结构纤维断裂规律。与常规的外推法一样，相邻单元法也是一种具有普遍适用性的方法。