立足构图 分类突破

邵乐华

[摘  要] 刚复习完某知识，学生面对考查此知识的复杂问题时却无从下手，这种现象经常出现. 文章以一道期末试卷压轴题为例，采用一定的教学手段，引导学生走出解题困境，并从中积累解题经验，促使他们提升数学核心素养.

[关键词] 压轴题;初中;教学;反思

在一次期末考试中，有一道压轴题，许多学生感到棘手，能全做对的学生少之又少. 刚复习完与此题相关的知识，为什么学生会一筹莫展呢？笔者对此题进行了认真研究，并思考了如下问题：如何引导学生走出解题困境？如何从中抽出基本几何模型？如何从中提炼基本数学思想方法？如何让学生从中积累解题经验，进而促进学生核心素养的提升？

原题再现

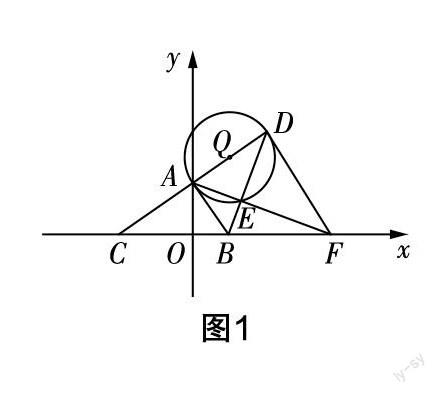
原题如图1所示，在平面直角坐标系xOy中，已知A（0，4），点B是x轴正半轴上一点，连接AB，过点A作AC⊥AB，交x轴于点C，点D是点C关于点A的对称点，连接AD，BD，以AD为直径作☉Q交BD于点E，连接AE并延长交x轴于点F，连接DF.

（1）求证：AE=AO;

（2）若AB-BO=2，求tan∠AFC的值;

（3）若△DEF与△AEB相似，求EF的值.

此题以平面直角坐标系为背景，把圆与三角形进行有机结合，考查全等三角形的判定与性质、相似三角形的判定与性质、勾股定理、锐角三角函数、等腰三角形的判定与性质、圆周角定理等数学主干知识. 同时，要求学生运用转化思想、数形结合思想、方程思想、分类讨论思想、模型思想解决问题. 其中第（2）题求tan∠AFC的值思维含量比较高，学生需要利用相似三角形的性质，逐步转化线段的比;第（3）题求EF的长，需要分类讨论，且每一种情况都需要找到与线段EF相等的线段. 那么解决此题，应如何构图、如何转化呢？有何规律？

解题教学

著名数学家华罗庚指出，解题退到最原始的状态，是解决问题的一个诀窍. 最原始的状态是什么呢？就是原题中的关键词，包括图形中的点与线段，图形的相对位置关系与数量关系，代数的特征与图形的对称性等，这些是数学思维的起点，既能促使解题思路自然形成，又揭示了解题方案的形成过程. 如“AC⊥AB”“点D是点C关于点A的对称点”“以AD为直径作☉Q”都是试题的重要信息，是思维的起点.

1. 审题

审题是解题的首要环节. 教学中，教师应重视审题环节，应引导学生学会审题. 问题的结构形式可以分为两种，一是并列式问题结构，即从原始题干出发，提出两个或多个并列的問题;二是递进式问题结构，即从原始题干出发，所提问题的难度不断增加，解决前一个问题能为解决后一个问题奠定基础.

2. 追本溯源

仔细品味这道题，会发现其基本素材源于教材的下面几个内容：

①如图2所示，AB是☉O的直径，∠ABT=45°，且AT=AB，求证：AT是☉O的切线;

②如图3所示，在Rt△ABC中，CD是斜边AB上的高，求证：△ACD∽△ABC，△CBD∽△ABC;

③如图4所示，AB=AC，∠A=40°，AB的垂直平分线MN交AC于点D，求∠DBC的度数.

命题人将教材的例、习题进行组合，把这些图形放在同一个图形中，并以平面直角坐标系为背景，将三角形、锐角三角函数与圆融合在一起. 对于原题的第（3）题，由于两个直角三角形相似时，直角必须对应相等，所以只需要分两种情况进行讨论.

3. 解法分析

对原题进行解法教学时，教师可提出如下3个问题.

问题1：解决平面直角坐标系中的几何问题时，应如何转化条件？

（预设答案：把点的坐标转化为对应线段的长，把斜放的直角三角形通过“改斜为正”转化为“一线三直角”模型，利用两坐标轴互相垂直构造直角三角形）

问题2：如何解决与圆相关的问题？

（预设答案：利用圆的性质，把有关圆的问题转化为三角形或四边形问题，然后利用三角形或四边形的性质求线段的长或角度）

问题3：如何求某个锐角的三角函数值？未指明对应关系的两个直角三角形相似，可能有几种情况？

（预设答案：欲求某个锐角的三角函数值，必须把这个锐角放置在直角三角形中，转化为直角三角形边与边的比. 当两个直角三角形相似时，可能有两种情况）

原题答案（1）因为点D是点C关于点A的对称点，AB⊥AC，所以AB是线段CD的垂直平分线. 根据线段垂直平分线的性质，得BC=BD. 根据等边对等角，得∠ACB=∠ADB. 又由条件易知∠BAC=∠BAD=90°，所以∠ABO=∠ABE. 因为AD是☉Q的直径，根据直径所对的圆周角是直角，得∠AED=90°. 所以∠AEB=90°. 因为∠AOB=∠AEB=90°，∠ABO=∠ABE，AB=AB，由角角边定理，得△ABO≌△ABE. 所以AE=AO.

（2）由（1）知△ABO≌△ABE，所以∠OAB=∠EAB. 根据同角的余角相等，得∠OAB=∠ACF，所以∠EAB=∠ACF. 又∠AFB=∠AFB，所以△AFB∽△CFA. 所以=. 设BO=x，则AB=2+x. 在Rt△ABO中，由勾股定理，得AB2=AO2+BO2，即（x+2）2=42+x2，解得x=3. 所以BO=3，AB=5. 所以tan∠ACF===. 设BF=3y，则AF=4y. 在Rt△AOF中，由勾股定理，得AF2=AO2+OF2，即（4y）2=42+（3y+3）2，解得y=或y=-1（不合题意，舍去）. 所以BF=，OF=. 在Rt△AOF中，由正切函数的定义，得tan∠AFC===.

（3）分两种情况讨论：①当△DEF∽△BEA时，∠BAE=∠DFE，所以AB∥DF. 所以∠ADF=∠CAB=90°. 过点F作FN⊥x轴，过点D作DM⊥y轴交y轴于点M，DM与FN交于点N，如图5所示，则四边形MNFO为矩形，∠DMA=∠COA=90°. 因为∠MAD=∠OAC，DA=CA，根据角角边定理，得△DMA≌△COA. 所以AM=AO=4，∠MDA=∠OCA. 因为∠ACB=∠ADB，所以∠MDA=∠ADB. 根据等角的余角相等，得∠FDE=∠FDN. 因为FE⊥BD，FN⊥MN，根据角平分线的性质，得EF=FN=OM=8. ②当△DEF∽△AEB时，∠FDE=∠BAE. 根据同角的余角相等，得∠BAE=∠ADB，所以∠ADB=∠FDE. 由等角的余角相等，得∠DAF=∠DFA. 所以AD=DF. 因为DB⊥AF，根据等腰三角形三线合一，得EF=AE=4. 综上所述，若△DEF与△AEB相似，EF的值为4或8.

评注解决第（2）题时，上述解法用到了两个相似模型，一是射影定理模型;二是反“A型”相似模型. 求线段长度时用到了两种基本方法，一是利用勾股定理建立方程求线段的长;二是利用相似三角形对应边成比例求线段的长. 在进行等比转化时，利用的是等角转化. 解决第（3）题时，上述解法首先应用分类讨论思想，把一个复杂的问题分解为两个小问题：△DEF∽△BEA与△DEF∽△AEB. 解决△DEF∽△BEA时，构建了“一线三直角”几何模型;解决△DEF∽△AEB时，构建了等腰三角形基本图形.

4. 模型、方法提炼

（1）全等模型

轴对称型：△AOB≌△AEB，△ACB≌△ADB，△EDF≌△NDF;

中心对称型：△AOC≌△AMD.

（2）相似模型

“三垂直”模型：△AOC∽△BOA∽△BAC;

“反A型”模型：△ABF∽△CAF;

“X型”模型：△AEB∽△FED，△AEB∽△DEF;

“一线三直角”模型：△MAD∽△NDF.

（3）特殊三角形模型

等腰三角形BCD，等腰三角形ADF，直角三角形ABC，直角三角形AOC，直角三角形AOB，直角三角形AED，直角三角形AOF，直角三角形MAD，直角三角形DNF等.

（4）运用勾股定理

在直角三角形中，已知一边及另外两边的关系，可以利用勾股定理求其他两边的长.

（5）等角对等比

比如，当∠OAB=∠ACF时，tan∠OAB=tan∠ACF.

5. 巩固提升

教学此题后，为了让学生巩固其中运用的知识、方法与技巧，教师可设计如下试题供学生练习.

（1）如图6所示，AB为☉O的直径，C，D是☉O上的两点，AC=BC，AD的延长线与CB的延长线交于点E. 若∠DAB=20°，求∠E的度数.

（2）如圖7所示，AB是☉O的直径，D是☉O上一点，DE是☉O的切线，过点B作BF⊥DE，垂足为F，分别延长AD，BF交于点C.

①求证：∠A=∠C;

②当BF=1，DF=2时，求☉O的直径.

（3）如图8所示，☉O是矩形ABCD的外接圆，∠ABC的平分线分别交AC，☉O，CD的延长线于点E、点F和点G，过点F作☉O的切线FH交CG于点H.

①求证：FH∥AC;

②若BA=BE，tan∠BAC=3，OE=2，求FH的长.

教后反思

1. 立足图形构造，为学生排忧解难

由于个体差异，学生解决同一问题时所出现的问题也有所不同，或知识断层，或没有发现隐含条件，或计算失误等. 教学中，教师应引导学生分步踩点得分，加强基本图形的构造，促使学生整合条件，利用图形思考与探究，进而把握解题的正确方向.

2. 加强变式练习，拓展思维空间

数学家希伯特指出，当解决一个问题时，一系列的新问题也随之诞生，当解题成功时，要善于提出新问题. 因此，教学中，教师不能就题论题，应深入领悟典型试题的编写意图，通过一题多解、一题多问、一题多变、多题一解等拓展学生的思维空间. 如本题就进行了一题多问、一题多变，使习题教学从浅层走向深层.

3. 关注思想方法，提升学生素养

数学思想是数学知识与方法的高度概括. 在教学中，教师应注重数学思想方法的提炼与渗透，从而提升学生的核心素养. 如本题教学渗透了转化思想、数形结合思想、方程思想及分类讨论思想.