数形结合思想在初中数学习题教学中的实践与思考

李 琰

(上海市国和中学，上海 200433)

一、关于初中数学“数形结合”思想的知识架构

数学思想是数学的灵魂。从某种意义上讲，学生怎样学习、怎样思考、用什么样的数学思想远比学习什么数学知识更重要。但在数学教学实践中，教师往往只注重讲解解题策略而忽略渗透数学思想。本文以初中数学综合题为载体，阐述“数形结合”思想在初中数学教学中的应用与渗透。

数形结合思想就是运用数的严谨和形的直观，将抽象的数学语言与直观的图形语言结合起来，使抽象思维和具象思维相结合，通过图形的描述、代数的论证来研究和解决数学问题的一种数学思想。“数形结合”是初中数学最重要的数学思想之一，很多教学内容中都有所体现，但要说起初中数学最能体现数形结合思想的数学知识，笔者认为有：直角坐标系、函数、锐角三角比、相似三角形以及勾股定理及其逆定理，这五部分知识中都自带“数”与“形”的属性。

二、关于初中“数形结合”思想的教学实践

初中数学被分为代数和几何两大分支，代数主要是对数与式的分析，而几何主要是对图形的研究。但教师需要通过思维引导、例题或练习设计、示范讲解等教学手段，让学生体会到代数与几何不是相互独立的，而是有着非常紧密的联系。很多代数问题直接计算运算量太大，甚至无从下手，但是如果转化成直观的图形之后，很容易通过图形的性质而得到解决。还有一些图形问题因为不会添加辅助线导致无法研究，但是往往通过坐标系的方法，转化成代数问题之后就很容易得到结果。数形结合是联系数与形之间良好的纽带，对于解决数学问题有着非常重要的作用，要让学生通过课堂体验、教师引导，形成“代数”“几何”灵活切换的意识，完成“数形结合”思想的渗透。[1]

1.界定“代数法”与“几何法”

笔者深感“数形结合思想”的博大精深，在教学实践中更是时刻铭记，不断尝试将“数形结合思想”融入日常教学、渗入学生的思维中。笔者在平时的习题教学中，常将例题和作业设计为一题多解，在例题讲解时，注意以代数、几何两种思路切入问题。主要运用方程(组)、函数解析式、运算公式等代数工具切入问题的方法，下文称之为“代数法”；主要以几何图形为思维支点，通过相似三角形、锐角三角比等几何手段切入问题的方法，本文称之为“几何法”。让学生形成一种条件反射，当一种思路遭遇瓶颈时，顺势转换思路，在“代数法”与“几何法”之间自由切换。

2.设计“可多角度切入”的综合问题

数学家波利亚说过：“一个专心备课、善于思考的老师能够拿出一个有意义但又不复杂的题目，去帮助学生挖掘问题的各个方面，通过这道题，就好像打开一扇窗，把学生引人一个完整的理论领域。”数学解题的有效性往往取决于问题本身的优劣，故习题教学中的题不在“多”而在于“精”和“透”。一个精挑细选的问题能够激发学生深入研究的兴趣，强化知识结构。同样，一道方法多样的题目能够加深学生对知识本质的理解，拓展思考问题的角度，提升思维品质。

在习题教学中培养学生的数形结合思想非常重要。为了更好地突显数形结合思想在数学问题中的作用，笔者设计了能充分运用“代数法”和“几何法”的函数综合题，带领学生将一道题充分“吃透”，在提问与思考的过程中，学生互为补充，从不同的角度切入问题从而激发出不同的解题思路。在综合问题的实践中，一题多解的教学才能“以一敌百”，将“数形结合”思想方法融会贯通，学生才能“百战百胜”。[2]

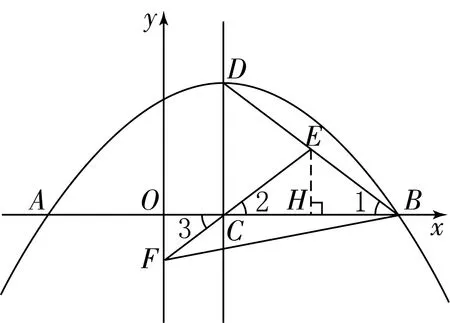
图1

例题：如图1，已知平面直角坐标系xOy，抛物线y=ax2+bx+2与x轴交于点A(-2，0)和点B(4，0)。

(1)求这条抛物线的表达式和对称轴；

(2)点C在线段OB上，过点C作CD⊥x轴，垂足为点C，交抛物线于点D，E是BD中点，联结CE并延长，与y轴交于点F。

①当点D恰好是抛物线的顶点时，求点F的坐标。

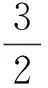
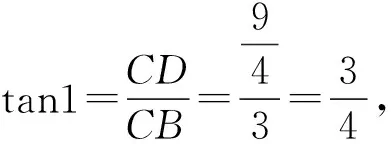
第(2)题第②小题亦是如此。

此时，教师可组织学生暂停解题，反思前面的思考过程，归纳“代数法”的优缺点，并适时点拨学生：当遇到“代数法”计算繁杂时，不妨转换思路，从观察图形入手，用“几何法”的灵动弥补“代数法”的不足。

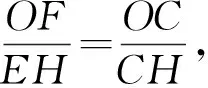
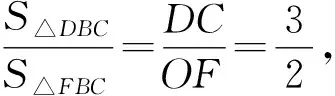
第(2)题第①②小题分别运用了“代数法”和“几何法”求解，贯通了直角坐标系、函数、锐角三角比、相似三角形等数学知识，运用了数形结合的数学思想方法，学生充分体会到“代数法”与“几何法”的优势和不足，更能感受到代数与几何互为补充、相辅相成的密切联系。

3.配合“有发挥空间”的作业习题

在“数形结合”专题的习题课中可以精讲以上的例题，当学生感到收获满满并且跃跃欲试时，教师可趁热打铁，布置一道“有发挥空间”的作业题或思考题。这道题的难度可略高于课堂例题，既可让学生将课堂所学充分运用，又比例题条件更丰富，比例题的切入角度更多，给学生课后留出自我提升的空间。以下是笔者的习题设计，供同行参考选用。

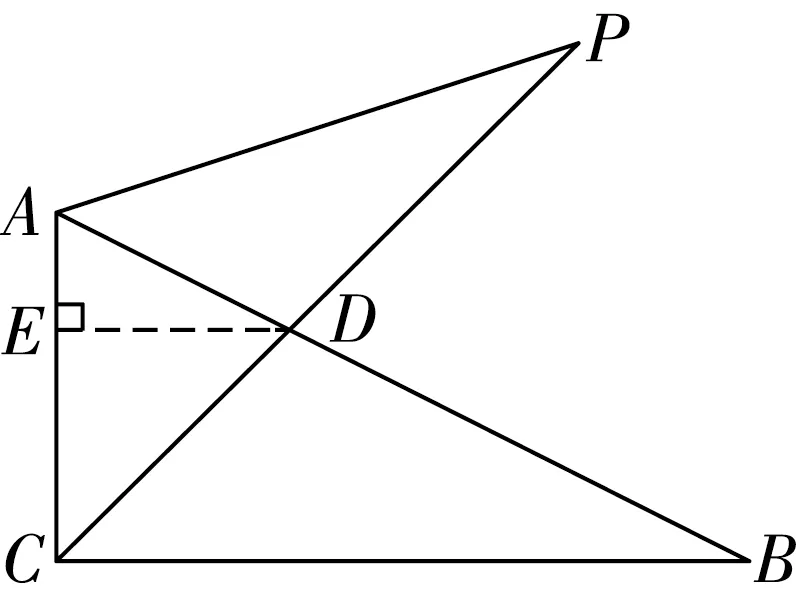
图2

习题示例：如图2，已知在△ABC中，∠ACB=90°，AC=1，BC=2，CD平分∠ACB交边AB于点D，P是射线CD上一点，联结AP。

(1)求线段CD的长；

(2)点M为边AB的中点，联结CM、PM，若△CMP是等腰三角形，求CP的长。

这道习题和例题不同，没有直角坐标系，也没有函数背景。笔者要求学生用多种方法解题，允许同学之间讨论、互相启发，并给足学生思考和回味的时间，这道作业题取得的教学效果可能超过了教师的预期。

罗增儒教授曾说，数学解题通常有四个自然阶段，审题、想题、写题、回题，即理解题意、思路探求、书写表达、回顾反思。其中思路探求就是从题目的条件出发，通过联想类似知识和已有经验，形成与结论之间的联系，它是解题思路形成的关键。[3]

第(2)题大部分同学也首先考虑从几何图形入手，由△CMP是等腰三角形的结论可假设：①CM=MP1或②CM=CP2或③CP3=MP3。

图3

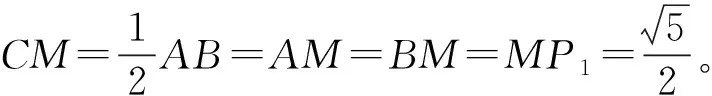
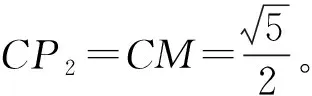
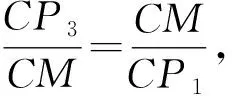
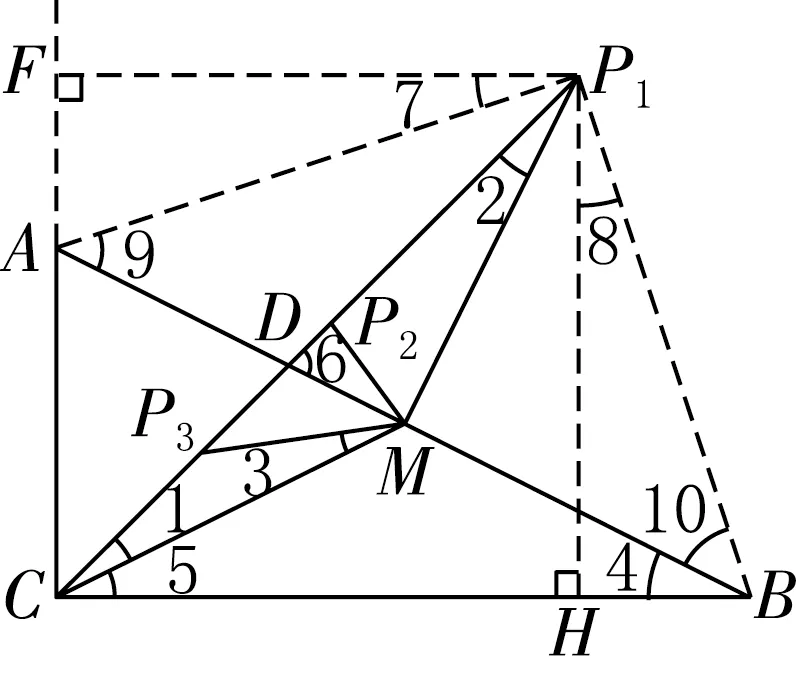
图4

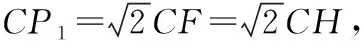
由于这道题是以几何图形的形式给出的，因此大部分学生都从“几何法”切入，但构造基本图形的策略不同，涉及的几何模块不同，列方程所依据的等量关系不同，所以出现了以上两种“几何法”。在习题讲解时，以上部分均可由学生表述，分享自己组合了哪些已知条件，如何联想到构造这样的基本图形，教师只要简要板书思维导图。

当学生都将此题定性为“几何问题”，只是借助代数方程进行必要计算时，教师可出其不意地提出问题：本题能用“代数法”求解吗？学生一筹莫展，教师可提示：本题与“代数法”之间是否相差了一个直角坐标系？学生恍然大悟：以“直角ACB”为切入点可建立直角坐标系。教师可组织学生当场进行小组讨论，合作完成以“代数法”解几何问题的初探(如下)。

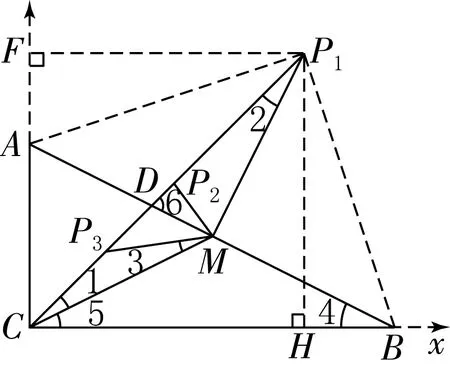
图5

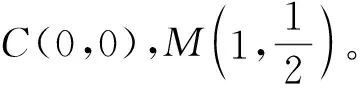
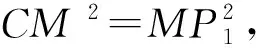
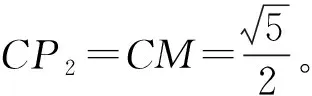
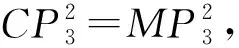
用“代数法”解几何问题，过程竟然出人意料的简便，教师应充分赞美学生勇于创新的精神以及将数形结合思想完美呈现的过程。两课时的习题研讨课很短暂，但对于数形结合的思考不能就此停止，教师可布置作业：希望学生反思并归纳“数形结合”专题研讨课的收获，回看并整理做过的几何综合题，挑选一至两题用建立直角坐标系的“代数法”进行求解。

三、关于初中教学“数形结合”思想的持续思考

1.“数形结合”思想的提出与发展

“数形结合”一词正式出现在华罗庚先生于1964年1月撰写的《谈谈与蜂房结构有关的数学问题》的科普小册子中，书中有一首小词：“数与形，本是相倚依，焉能分作两边飞？数无形时少直觉，形少数时难入微。数形结合百般好，隔离分家万事非；切莫忘，几何代数统一体，永远联系，切莫分离！”这首小词生动、深刻地指明了“数形结合”的价值，也揭示了“数形结合”的本质。“数形结合”是一种重要的数学思想，也是一种智慧的数学方法。我们在研究抽象的“数”的时候，往往要借助直观的“形”，在探讨“形”的性质时，又往往离不开“数”。通过“数”与“形”的结合，我们对事物规律的把握就能既容易又准确、深刻。[4]

2.“数形结合”思想的探索与发现

在初中数学综合题的探索过程中，常用的思维路径有两条，一是“以数解形”，二是“以形助数”，本文中分别称之为“代数法”与“几何法”。

(1)对“数”“形”的联想与转化，是运用“数形结合”思想的关键。如果图形中已经建立了直角坐标系，自然联想到把几何中的点、线等基本元素与代数中的数、方程(组)等基本元素对应起来，即将几何元素转化为求解点的坐标、函数的解析式、方程(组)等，从而获得解决路径，这样的方法是“以数解形”，本文称之为“代数法”，也就是笛卡尔所创立的“解析几何法”。“代数法”的优势是思维路径简洁，答案准确，不易漏解，一个等量关系稍作变式即可反复使用，一种思路常常可同时解决几个问题；“代数法”的缺点是计算过程较繁琐，易出现计算错误。

“几何法”的优点是不需繁杂的计算，常有出奇制胜的效果。但“几何法”的难点是图形变化比较灵活，学生需要对图形有较强的观察能力，对组合条件有较强的联想能力，对基本图形及其相关解法有较深厚的积累，才能添加辅助线构造出基本图形，从而寻找边角关系，并借助恰当的代数工具进行准确计算。其缺点是常常需要“移步换景”，即每个问题要添加不同的辅助线，更换不同的基本图形，发现不同的解决思路，这对学生的读图构图能力、逻辑思维能力要求较高。

(2)完善习题教学的各环节，是落实“数形结合”思想的重要手段。一是设计优质问题，渗透“数形结合”思想。“好题”的“好”主要在于它可以进一步展开和一般化，蕴含丰富多彩的解决方法和知识内容。要在习题教学中逐渐渗透数学思想，选择一道“好题”尤为重要，以这一道题为载体，通过多角度的审视、多层次的思考、多方法的解决，以“一道题”关联“一个体系”，从而达到“做一道、会一类、通全部”的目的。能一题多解的综合题无疑是“好题”中的好题，这种例题与习题既能兼顾到各类层次的学生，关注到各种思维的差异，也能多角度地分析条件，有助于探究问题的深层结构。另外，一题多解的过程中蕴含着不同的原理，沟通着不同的知识，有助于形成优化认知结构、明晰知识框架、渗透“数形结合”思想的教学过程。二是合理引导思维，提炼“数形结合”思想。教师在课堂上要善于引导学生联想与思考。教师在教学过程中引导学生从多种角度思考问题，从条件的不同组合切入问题，从而实现一题多解。由于不同学生之间思维方式、思维深度和思考问题的经验不同，基于“形”的条件联想的方向也会不同。笔者认为，在习题教学中，教师不应刻意追求多解，而应引导学生分析已知条件，特别是请学生分享方法是如何想到的，基于学生的思维特点和经验，注重联想方向的合理性，尊重思维的多样化，自然会得到一题多解的局面。当思维的火花被充分激发和碰撞后，教师顺势引导学生自主提炼数学思想方法，这样提炼出的数学方法才能完成内化，才能一般化地运用到不同的问题中，这样基于自身体验提炼出的数学思想才能深植学生心中。[5]三是持续发展思维，深化“数形结合”思想。数学家亚诺斯卡娅说过：“解题就意味着把所要解决的问题转化为已经解决的问题。”短短两课时的习题教学一定不能解决“数形结合”的所有问题，但通过对例题和练习题条件图形的对比与归纳，对所有解法的反思与比较，对基本问题模型的归类与再思考，学生可以再次回味“数形结合”思想，从而使不同的问题“归一”为“数形结合基本型”问题，进一步深化“数形结合思想”。