高超声速圆锥边界层转捩实验研究
徐席旺, 易仕和, 张 锋, 郑文鹏, 米 琦
(国防科技大学空天科学学院, 湖南长沙 410073)
引 言
高超声速边界层转捩可导致飞行器表面热传递、 摩擦阻力以及其他边界层特性发生重大改变, 从而直接影响到高超声速飞行器气动布局、 热防护系统的设计与优化等方面, 一直是相关研究的热点[1]. 转捩是指边界层从层流发展为湍流的这一过程. 边界层转捩机理非常复杂, 层流-湍流转捩的路径与边界层中初始扰动的高低相关, 一般可将转捩路径分为5条[2], 在初始扰动水平较低的情况下, 边界层转捩主要与边界层的不稳定性相关, 此时, 模态增长是导致边界层转捩为湍流的主导因素.
Mack[3]早在20世纪七八十年代开创性地利用线性稳定性分析对边界层的不稳定性进行了系统的研究, 并发现在Ma>2.2时, 边界层内除了第1模态不稳定波外, 还有在壁面和当地声速线之间来回反射的第2模态波. 第1模态为涡波扰动, 与不可压缩流动中的T-S波类似; 第2模态为声波扰动, 当Ma>4时在边界层转捩中占据主导地位. 尤其是对于0°攻角条件下的尖锥高超声速边界层, 第2模态波的模态增长是导致边界层从层流转捩为湍流的主导因素[4].
在Mack预测了第2模态波的存在后, 大量学者对第2模态波进行了详细的研究. 1974年Demetriades[5]通过热线测试技术对Ma=8条件下5°半锥角的尖锥模型边界层内不稳定波进行了测量, 在实验中定量测量证实了高超声速圆锥边界层中Mack第2模态波的存在. 此后Demetriades[6]进一步通过阴影技术直接观察到了圆锥表面的第2模态波. 受当时流动显示技术的制约, 并没有获得清晰的第2模态波结构. 进入21世纪后, 第2模态波的研究也得到了更加深入的探索. Casper等[7]在Sandia高超声速风洞内采用高速纹影技术对Ma=5, 8条件下的半锥角为7°的直圆锥边界层转捩进行了实验研究, 得到了第2模态波的纹影图像, 并分析了第2模态波不稳定性增长和破碎为湍流斑的过程. Kennedy等[8]同样采用高速纹影技术对Ma=10, 14条件下的半锥角为7°的尖锥边界层内第2模态不稳定性进行了流动显示研究, 得到了十分清晰的第2模态波的纹影图像; 并采用一种将空间信息转化为时域信息的方法对纹影结果进行了定量分析, 得到了基于第2模态波纹影图像的N值分布, 并将其与根据PCB压力传感器数据计算的N值分布进行了对比, 此外还将实验计算的N值与线性稳定性理论的分析结果进行了对比, 结果表明在最大放大频率上具有很好的一致性. 国内, 中国空气动力研究与发展中心的陈苏宇等[9]在FD-14激波风洞内同样采用高速纹影在Ma=8, 10条件下开展了7°钝锥边界层转捩实验, 捕捉到了第2模态波和湍流斑的空间结构, 并对纹影图像的灰度分布进行了功率谱密度(power spectral density, PSD)分析.
由于纹影技术本身存在的光路积分效应, 无法得到某一流场切片内的第2模态波分布. 为此研究人员利用对激光片光内流场成像的技术对第2模态波进行了流动显示, 此类技术主要有基于CO2冷凝的滤波Rayleigh散射技术和基于纳米粒子示踪的平面激光散射(nano-tracer-based planar laser scattering, NPLS)技术. Zhang等[10-12]利用基于CO2冷凝的滤波Rayleigh散射技术对高超声速圆锥表面边界层流动结构进行了实验研究, 获得了Ma=6条件下圆锥表面边界层从层流发展出现第2模态波并最终转捩为湍流的完整流动显示过程. 但根据滤波Rayleigh散射的结果仅可观察到第2模态波的外轮廓. Liu等[13-14]利用NPLS技术对圆锥边界层进行流动显示研究时得到了十分清晰的第2模态波的“绳状”结构.
除流动显示技术外, 研究人员还通过多种技术手段对圆锥边界层内的第2模态波进行了深入的研究. Stetson等[15-18]采用热线测试技术在常规高超声速风洞中对来流Ma=8、 半锥角7°的圆锥边界层稳定性特征进行了详细实验研究, 分别从头部钝度、 攻角、 来流单位Reynolds数以及壁温等方面进行了深入研究, 分析了多种不同因素对边界层转捩的影响规律, 发现边界层内主要不稳定波是第2模态波. 但这一规律并非在所有情况下均满足, Bountin等[19]同样用热线实验研究了Ma=6尖锥边界层扰动演化规律, 发现在转捩过程中起决定作用的是Mack第1模态. 而Schneider等[20]在对钝锥高超声速边界层稳定性及转捩特性进行研究时发现, 在钝锥边界层转捩过程中, 第1模态和第2模态都有可能占据主导作用.
Marineau等[21-22]采用高频压力传感器(PCB-132A31)对7°尖锥和钝锥边界层稳定性进行了实验研究, 分析了攻角、 头部钝度等对边界层内第2模态不稳定性的影响. Zhang[12]利用粒子图像速度测量(particle image velocimetry, PIV)技术对0°攻角条件下的裙锥高超声速边界层内的第2模态波进行了实验研究, 实验结果证明第2模态波是纵声波. Si等[23]在Ma=6风洞内通过Rayleigh散射流动显示、 快响应压力传感器和红外热成像技术研究了波纹壁对裙锥高超声速边界层转捩和气动加热的影响, 其结果表明波纹壁可抑制第2模态不稳定性, 并消除转捩前的局部加热, 同时其研究结果进一步证实了转捩前出现的局部加热区域是由第2模态不稳定性所引起的. 刘小林等[24]在Ma=6 低噪声风洞内利用高频压力传感器(PCB-132A31)对半锥角为7°的直圆锥边界层转捩进行了实验研究, 分析了不同单位Reynolds数、 自由来流湍流度对第2模态波的影响, 并分析了1°攻角条件下迎风面与背风面中第2模态波的发展规律.
根据前述的大量研究可见, 圆锥是研究第2模态波的主要模型, 而理解第2模态波的相关特性是解决边界层转捩问题的重要部分. 为深入探究第2模态波占主导的圆锥高超声速边界层转捩的流场精细结构变化、 以及其表面高频脉动压力和温度分布情况, 拟在高超声速静音风洞内通过NPLS、 高频脉动压力测试技术以及TSP技术开展0°攻角条件下不同单位Reynolds数的圆锥边界层转捩实验.

1 实验设备与测试技术
1.1 实验设备
实验在国防科技大学空气动力学实验室的高超声速静音风洞(见图 1)内进行. 该风洞采用吹吸式运行, 喷管设计Ma=6, 出口直径为300 mm. 风洞稳定段最大总压5 MPa, 最大总温600 K. 该风洞有静音和低噪声两种运行方式, 在喉道抽吸开启的状况下, 喷管出口流动为静音状态, 在喉道抽吸关闭的状况下, 喷管出口流动为低噪声状态. 静音状态下, 其噪声水平σ约为0.1%[25]. 考虑到静音条件下边界层转捩难以发生, 本文实验均在抽吸关闭的状况下开展.

图1 高超声速静音风洞Fig. 1 Hypersonic quiet wind tunnel
1.2 实验模型
实验模型为半锥角为7°的直圆锥, 如图 2所示. 模型采用分段加工, 圆锥主体保持不变, 头部可更换, 两段连接处圆锥主体的横截面直径为35.69 mm, 主体轴向长度为396.70 mm. 使用头部钝度半径为R<0.1 mm的尖锥头部时, 圆锥总长为542 mm.
在建立坐标系时, 将坐标原点设在圆锥头部和圆锥主体连接处,x轴沿圆锥母线并指向下游,y轴为该圆锥母线坐标原点处的表面外法线.

图2 圆锥模型示意图Fig. 2 Schematic diagram of the cone model
对于3种不同测试技术, 加工了不同材质的圆锥模型. 用于NPLS实验的圆锥模型采用碳钢加工, 并对其表面采用发黑处理以减弱激光片光导致的壁面散射光. 用于脉动压力测量实验的模型采用铝合金加工, 并对圆锥后段中间进行掏空处理. 在一条母线上布置了10个PCB传感器测孔, 测点坐标分别为x1=30 mm,x2=90 mm,x3=140 mm,x4=180 mm,x5=210 mm,x6=240 mm,x7=270 mm,x8=300 mm,x9=330 mm,x10=360 mm.用于TSP实验的圆锥模型, 采用电木加工, 其热传导系数为k=0.19 W/(m·K), 密度为ρ=1 200 kg/m3, 比热容为c=1 464 J/(kg·K).这3类模型仅材质不同, 尺寸大小等完全一致.
1.3 NPLS技术
NPLS技术是一种高时空分辨率的流动显示技术[26],图3为NPLS系统组成示意图. 该系统通过在风洞稳定段上游加入名义直径为50 nm的二氧化钛(TiO2)粒子, 在实验段通过激光片光照亮均匀混合有纳米粒子的流场, 同时通过CCD相机捕捉纳米粒子的散射光, 从而达到流动显示的效果. NPLS已被广泛应用于超声速/高超声速流动显示之中, 具有十分优良的测试性能[27-29]. 本文所用NPLS系统的光源采用双腔Nd:YAG脉冲激光器, 该激光器可产生两束波长为 532 nm、 脉宽为6 ns 的激光, 其最大能量为380 mJ; 成像系统采用 Imperx跨帧CCD相机, 其分辨率为2 048 pixel×2 048 pixel, 灰度等级为4 096, 跨帧时间为5 μs.

图3 NPLS系统示意图Fig. 3 Schematic diagram of the NPLS system
1.4 高频脉动压力测试技术
高频脉动压力测试系统主要由高频脉动压力传感器和高频数据采集器组成. 本文传感器采用PCB-132 A31型压电传感器, 其测量频率响应范围为11 kHz~1 MHz, 最小压力分辨率为7 Pa, 本文使用的传感器平均灵敏度约为21 mV/kPa. 数据采集器采用DH5960超动态信号采集系统, 其采样频率最高可达20 MHz, 本研究中采样频率均设置为5 MHz.
高频脉动压力测试系统所得的信号为脉动压力时序信号. 时域信号中难以直接获得较为有价值的规律. 一般通过PSD将时域信号转化为频率域信号进行分析. 功率谱密度分析是信号处理中常用的一种方法, 其计算方法也有多种, 是一种较为成熟的信号处理方法, 本文采用其中经典的Welch方法进行计算. 窗函数采用Blackman窗, 快速Fourier变换(fast Fourier transform, FFT)长度为4 096, 重叠率为50%.
图4为风洞运行前和运行时所测量的圆锥表面脉动压力的功率谱密度结果, 由于PCB传感器测量下限频率为11 kHz, 故 11 kHz 以上的信号为有效信号, 可见, 对于有效信号的功率谱结果, 系统白噪声中各频率成分占比基本一致, 功率谱密度曲线分布较为平稳, 而风洞运行时, 边界层中包含不稳定波, 这些不稳定波具有特定的频率波段, 将导致壁面脉动压力能量分布不均, 出现特定频率波段的波峰. 在该组实验状态下风洞运行时, 脉动压力信号在115 kHz处取得峰值. 进一步根据其频率特征等信息可对该波峰信号进行分析, 可以判断出该不稳定波的类型以及其特有的相关信息, 结合圆锥表面边界层发展的过程以及其他相关研究可以初步判断出该不稳定波为边界层中的第2模态波.

图4 脉动压力功率谱密度图Fig. 4 Typical PSD results

eN方法是一种基于线性稳定性理论对扰动波N值进行计算, 从而判断转捩的转捩预测方法[30-31]. 本文对PSD结果中不同频率对应的N值进行计算, 计算公式为
(1)
其中,N为第i个测点处对应的N值, PSD0为最靠近上游的传感器(第1个传感器)测得的脉动压力的功率谱密度值, PSDi为第i个测点处传感器测得的脉动压力的功率谱密度值.
1.5 TSP技术
TSP技术通过温敏荧光材料反射的光强信息来获得模型表面温度分布. 温敏荧光材料在光源的照射下会发出特定波长的激发光. 该激发光的光强会随温敏材料表面的温度升高而降低. 对光强与温度之间的关系进行标定, 可得到模型表面的温度分布. 本文所用的TSP系统由TSP涂层、 激发光源、 CCD相机和滤波片组成. 关于该系统更详细的信息可参考文献[32-33]. TSP涂层由荧光分子和粘结剂组成. 荧光分子由长春应用化学研究所研制, 粘结剂采用聚乙烯醇缩丁醛(PVB). 将荧光分子粉末溶解在PVB溶液中, 形成TSP涂层. 然后, 使用喷笔(0.2 mm出口)将TSP涂层喷在模型上. 激发光源为单波长365 nm的UV-LED. 滤波片采用的是460 nm的长波通滤波片.
文献[32]中对该TSP涂层进行了静态标定, 得到了如图 5所示的标定曲线. 并得到了标定方程为
其中,I和T分别为风洞运行时模型表面的光强和温度,Iref和Tref分别是风洞运行前测量的参考光强和参考温度. 将标定曲线与TSP噪声水平相结合, TSP的温度分辨率在0.5 ℃左右.

图5 TSP标定曲线[32]Fig. 5 Calibration curve for TSP[32]
2 实验结果
2.1 NPLS结果
图6为光滑尖锥在0°攻角、Re=1.2×107m-1条件下某条母线上的流场切片的精细结构NPLS流动显示结果.图中主流方向为从左至右, 流动显示的流向范围约为278~400 mm,图片空间分辨率约为98 mm/pixel.
图6中边界层从第2模态波发展为湍流的过程清晰可见. 在x=320 mm之前, “漂浮”于边界层外缘的“绳状”第2模态波结构清晰可见. 与第2模态波的纹影显示结果[7-9]以及滤波Rayleigh散射结果[10-12]相比, NPLS技术所得到的第2模态波结构更加清晰细腻, 除了显示其外轮廓, 还可更进一步地反映第2模态波的内部结构.
根据图6的空间分辨率以及相应结构在图中所占有的像素点数量, 可以估算得到其空间尺寸大小. 根据该方法可以估算得到x=280~320 mm之间第2模态波的平均流向波长约为3.62 mm, 边界层的平均厚度约为1.67 mm. 故根据该NPLS结果可得, 第2模态波的波长约为当地边界层厚度的2.17 倍, 这与Mack[3]根据线性稳定性理论分析得到的“第2模态波波长约为当地边界层厚度的2倍”这一规律基本一致.

图 6 尖锥边界层流向NPLS结果(Re=1.2×107m-1)Fig. 6 Streamwise NPLS image of the sharp cone boundary layer(Re=1.2×107 m-1)
图6显示, 边界层发展至x=320 mm后, “绳状”第2模态波结构开始消失不见, 边界层中“涡结构”被拉长、 变形. 由于缺乏直接根据流动显示结果确定边界层转捩起始位置的判据, 本文将第2模态波消失到小涡结构开始出现这段区域定义为过渡区, 表示边界层由线性增长阶段发展到湍流的过程. 故图 6中过渡区域大致为x=320~368 mm. 在x=368 mm 附近边界层中开始出现小涡结构, 继续往下游发展, 边界层内涡结构变得更加复杂, 出现众多大涡和小涡结构, 因此认为其已发展成为湍流.
在研究台阶对高超声速圆锥边界层转捩的影响时, 作者采用了一种基于NPLS图像灰度值信息分布的定量分析方法[34]. 采用同样的方法对图6所示状态下的NPLS结果进行分析, 同时为了对比边界层在不同发展阶段(层流、 第2模态波和湍流)所得到的结果之间的差异将流动显示范围增加至约为x=200~400 mm, 如图 7所示, 并给出了两幅时间相关的NPLS结果.图 7中上下两幅图片的时间间隔为5 ms,图片空间分辨率与图 6 尖锥边界层流向NPLS结果(Re=1.2×107m-1)相同.图 7中可见, 边界层在x=225 mm之前的区域看不到明显的第2模态波结构, 从x=225 mm 之后NPLS结果中“绳状”第2模态波结构可被明显观察到; 发展到x=275 mm 附近第2模态波的结构变得更加清晰, 在x=320 mm之后“绳状”第2模态波结构消失不见, 边界层进入“过渡区”; 在x=368 mm附近开始完成转捩发展成为湍流.

图7 尖锥边界层时间相关的流向NPLS结果(Re=1.2×107 m-1)Fig. 7 Temporally-correlated streamwise NPLS image of the sharp cone boundary layer(Re=1.2×107 m-1)
故提取平行于壁面且距壁面高度约为y≈1.18~1.28 mm的截线上的灰度值信息, 并根据前述的不同发展阶段, 将其分为5个阶段进行PSD分析. 其中, 第1段为x=200~225 mm, 第2段为x=225~275 mm, 第3段为x=275~320 mm, 第4段为x=320~368 mm, 第5段为x=368~400 mm.
图 8所示为5个阶段分别对应的基于NPLS图像灰度值信息的PSD曲线.图中可见, 第1段由于NPLS结果中未出现明显的“波结构”, 基于NPLS图片灰度值信息所计算得到的PSD曲线仅在30 kHz 附近出现有一个峰值, 更高频率的成分占比基本为零.

图8 基于NPLS图像得到的PSD曲线Fig. 8 PSD curves from NPLS images
在第2阶段中, 第2模态波结构可被观察到, 但其形状并非特别清晰, 此时得到的PSD曲线中在200~300 kHz之间出现有一个幅值较小的波峰.根据图 7中NPLS图像进行时间相关性分析, 可以得到: 在x=225~275 mm之间, 第2模态波的平均传播速度U≈653.4 m·s-1、 平均波长λ≈2.9 mm, 由此可估算得, 在该区域内第2模态波的特征频率f≈U/λ≈225.3 kHz. 这与图 8中PSD曲线反映的特征频率均处于200~300 kHz范围内, 但在PSD曲线中200~300 kHz的波峰中存在两个小尖峰, 出现该现象的原因可能是本文实验所得的NPLS图片空间分辨率太低, 单个第2模态波结构中包含的像素点较少, 导致计算得到的PSD曲线较为粗糙.
在第3阶段中, 第2模态波结构十分清晰, PSD结果中第2模态波峰值也更大, 与第2阶段相比第2模态波的频率有所下降. 在第4阶段中, 第2模态波已经消失, PSD曲线中也已看不到相应的波峰, 在低频部分占比明显增多. 而在第5阶段中, 由于NPLS结果中已开始逐渐变成湍流, 截线上的灰度值分布情况较为复杂, 计算得到PSD曲线也更加复杂.
为进一步对比不同头部钝度条件下的圆锥边界层转捩情况, 选取头部钝度半径为R=1.67 mm的钝锥头部装配后进行了相关实验.图 9所示为Re=1.15×107m-1时0°攻角钝锥母线上的NPLS结果.图中可见, 当头部钝度半径增加至1.67 mm后在该单位Reynolds数条件下, 边界层始终保持为层流状态, 边界层转捩被大大推迟.

图9 钝锥边界层流向NPLS结果(Re=1.15×107 m-1)Fig. 9 Streamwise NPLS image of the blunt cone boundary layer(Re=1.15×107 m-1)
增大来流Re=1.65×107m-1, 所得结果如图 10所示. 在此条件下可观察到钝锥模型表面边界层由层流发展至第2模态波出现、 消失, 最终转捩为湍流的完整过程. 在x=300~325 mm 之间第2模态波形状清晰可见. 继续往下游发展, 可以看到在x=330~343 mm之间边界层的形态呈现为一个波长较长的形状类似于“发卡涡”的大涡结构. 该大涡结构是在第2模态波消失以及边界层转捩成为湍流这一阶段内出现的, 且其波长约为第2模态波波长的5倍, 或者更长, 可能是边界层中出现的第1模态波, 但还需更加深入的研究来加以验证. 根据相关研究表明, 在圆锥边界层转捩过程中, 第2模态波发展速度快, 但会出现先增长后衰减的发展趋势; 而第1模态波则处于缓慢增长的过程之中, 在转捩末期, 逐渐衰减的第2模态波同已增长的第1模态波发生相互干扰, 从而进一步促进边界层转捩成为湍流. 在钝锥边界层中, 边界层发展速度明显慢于尖锥, 这可能导致钝锥边界层中第1模态发展更为充分, 从而在流场精细结构中在第2模态波和转捩为湍流之间出现有疑似第1模态波的大涡结构. 其后, 边界层中出现“静区域”, 边界层厚度先变薄, 在x=350 mm附近变为最薄, 而后又开始增厚, 最终在x=365 mm处开始大涡结构, 并逐渐破碎成为小涡结构, 边界层转捩成为湍流.

图10 钝锥边界层流向NPLS结果(Re=1.65×107 m-1)Fig. 10 Streamwise NPLS image of the blunt cone boundary layer(Re=1.65×107 m-1)
继续增大来流Re=1.75×107m-1, 所得结果如图 11所示.图中可以看到边界层在x=240~250 mm 之间出现有比较模糊的第2模态波. 在x=300~330 mm之间出现一个大涡结构(波长约为x=240~250 mm之间出现的第2模态波的波长的5倍以上), 其后边界层突然变薄, 发展进入“静区域”, 在x=330~335 mm之间边界层厚度仅约为0.2 mm. 在强剪切力以及强非线性作用下, 边界层迅速开始增厚, 然后迅速破碎为湍流.

图11 钝锥边界层流向NPLS结果(Re=1.75×107 m-1)Fig. 11 Streamwise NPLS image of the blunt cone boundary layer(Re=1.75×107 m-1)
钝锥边界层转捩与尖锥相比更加困难, 但随单位Reynolds数变化, 边界层转捩的发展规律一致: 均表现为随单位Reynolds数增加, 边界层转捩提前.
为进一步对钝锥边界层中出现的第2模态波以及“大涡结构”进行定量分析, 将Re=1.65×107m-1时的NPLS进行了时间相关性分析. 如图 12所示为时间间隔为5 μs的两幅时间相关的钝锥边界层NPLS图像. 对于该时间相关的NPLS结果, 采用基于流场灰度信息的零均值互相关[35-36](zero mean normalized cross-correlation, ZNCC)算法对钝锥边界层中出现的绳状第2模态波以及狭长的大涡结构的速度信息进行了提取.
基于流场灰度信息的零均值互相关算法是一种基于时间相关NPLS图像进行流场速度测试的方法[35]. 该算法的核心表达式如式(2)所示.
CZNCC=
(2)
式中,CZNCC为根据选定流场区域的灰度相关信息获得的相关系数, 其最大值为1, 相关系数越大, 两幅图像中选定区域的匹配程度越高.f(x,y)和g(x,y)分别表示时间相关的两幅图像中选定区域的灰度值, (xi,yj)和(x′i,y′j)为两幅时间相关的图像中选定区域内的点的像素坐标,m为选定的图像匹配窗口大小的1/2, 上标′-′表示均值.
在图 12中a与b分别为给定的第2模态波和狭长的大涡结构所在区域进行零均值互相关计算的选定区域, 其中a1与b1作为参考区域, 是在进行计算前人为选定的一个矩形区域;a2与b2则是进行零均值互相关计算后得到的第2时刻的图像中与参考区域相关性最大的目标区域.

图12 钝锥边界层时间相关的流向NPLS结果(Re=1.65×107 m-1)Fig. 12 Temporally-correlated streamwise NPLS image of the blunt cone boundary layer(Re=1.65×107 m-1)
进行零均值互相关计算后可得到参考区域与目标区域在水平和垂直两个方向移动的像素距离. 根据零均值互相关计算结果,图 12中第2模态波附近的a区域沿x方向移动的距离为37 pixel, 沿y方向移动的距离为0; 而狭长的大涡结构附近的b区域沿x方向移动的距离为26 pixel, 沿y方向移动的距离同样为0. 再结合该组NPLS结果的空间分辨率为99 μm/ pixel, 则可得到a区域沿x方向移动的距离为3.663 mm,b区域沿x方向移动的距离为2.574 mm. 根据两组图像的时间间隔为5 μs, 可得到a,b区域的移动速度分别为Ua=732.6 m/s,Ub=514.8 m/s.
进一步根据a,b区域附近的第2模态波以及大涡结构所占的流向像素长度可估算得到a区域附近的第2模态波波长λa≈3.27 mm, 同时还可估算得此处边界层厚度δa≈1.68 mm, 即此处绳状结构的波长约为当地边界层厚度的1.95 倍, 根据Mack[3]指出的“第2模态波波长约为当地边界层厚度的2倍”, 可表明此处得到的绳状结构为第2模态波. 而b区域则由于空间分辨率太大, 无法清晰地判断其起始位置, 但根据其与最底层边界层的区别可估计其波长不低于16.35 mm.
由此可估算得, 在a区域附近的第2模态波的特征频率fa≈Ua/λa≈224 kHz,b区域附近的狭长的大涡结构的特征频率fb≈Ub/λb≈31 kHz (或者更低).该结果表明: 该单位Reynolds数下, 在钝锥边界层中首先发展起来的是特征频率在200 kHz附近的第2模态; 但随着边界层的继续发展, 第2模态波将逐渐消失. 在第2模态波消失之后, 边界层中出现特征频率在30 kHz量级的狭长大涡结构.
2.2 PCB结果
为进一步研究圆锥壁面边界层压力脉动分布情况, 采用PCB 132A31高频压力传感器在不同单位Reynolds数条件下开展了尖锥母线不同测点的压力脉动p′测量实验.图13所示为Re=1× 107m-1时0°攻角下尖锥母线上脉动压力的PSD分布曲线. 在进行功率谱密度计算时均按照Marineau等[21]采用的方法: 将风洞运行测得的脉动压力功率谱密度减去运行前采集的系统白噪声的功率谱密度, 从而减少系统白噪声的影响.

图13 尖锥表面脉动压力的PSD(Re=1×107 m-1)Fig. 13 PSD curves of the sharp cone(Re=1×107 m-1)
由图13可见, 前4个测点(x=180 mm之前)的功率谱密度曲线中并未出现有任何明显特征的波系, 此时边界层中扰动仍处于线性发展的初始阶段. 从第5测点开始出现第2模态波, 其特征频率和幅值分别约为: 219 kHz和0.152 1. 第6测点第2模态波特征频率 206 kHz, 幅值上升为0.239 6. 第7测点在195 kHz处取得第2模态波的峰值, 约为0.316 1. 第8测点处, 第2模态波幅值继续增长约为0.543 1, 特征频率下降为187 kHz. 在第9测点处, 第2模态波幅值达到了最大值, 约为0.739 0, 特征频率继续保持下降, 约为184 kHz. 第10测点处, 第2模态波出现了大幅衰减, 在特征频率为179 kHz处, 峰值约为0.218 7. 该PSD结果表明第2模态波在沿流向发展过程中, 特征频率逐渐降低、 幅值则出现先增大后减小的发展趋势.
图 14所示结果为Re=1.3×107m-1时尖锥边界层内脉动压力的PSD结果. 为了使各测点之间的PSD曲线得到更加清晰的展示, 将各测点的PSD曲线分开绘制.图中s表示x方向测点编号, 第1测点对应x=30 mm.图中可见, 前3个测点PSD曲线中并无明显波系结构出现, 第4测点在特征频率约为251 kHz附近出现幅值约为0.178 4 的第2模态波. 第5测点处, 第2模态波幅值增长为0.504 88, 特征频率下降为242 kHz. 发展到第6测点, 第2模态波幅值达到最大, 约为 0.535 2, 特征频率下降为232 kHz. 第7测点处, 第2 模态波幅值衰减为0.329 1, 特征频率继续下降为218 kHz. 发展至第8测点, 第2模态波信号已消失, PSD曲线中低频成分占比开始明显增多, 继续往下游发展, 低频成分占比逐渐增加, 呈现为典型的湍流形态.

图14 尖锥表面脉动压力的PSD(Re=1.3×107 m-1)Fig. 14 PSD curves of the sharp cone(Re=1.3×107 m-1)
当Re=1.5×107m-1时, 脉动压力PSD结果如图 15所示.图中可见, 随着单位Reynolds数的增加, 在第3测点处便可观察到第2模态波, 发展到第5测点第2模态波幅值达到最大. 第6测点第2模态波信号已经消失, PSD曲线中低频成分开始增多, 其后的测点也均无明显特征信号, 均表现为低频成分占主导. 同时可见, 往下游发展低频成分占比逐渐增加.

图15 尖锥表面脉动压力的PSD(Re=1.5×107 m-1)Fig. 15 PSD curves of the sharp cone(Re=1.5×107 m-1)
对钝锥模型也开展了3种不同单位Reynolds数条件下的脉动压力测量实验. 如图 16所示为钝锥模型表面脉动压力的PSD结果. 其中,图 16 (a)中显示, 当Re=1×107m-1时, PSD曲线中无明显特征信号, 与尖锥PSD结果中第2模态波出现之前的曲线相似, 表明在该单位Reynolds数条件下, 钝锥模型在测量范围内均处于层流状态.图 9中单位Reynolds数与图 16 (a)接近, 同样直接反映了边界层在此条件下始终处于层流状态.
当Re=1.65×107m-1, 所得结果如图 16 (b)所示.图中可见, 第8测点处开始出现微弱的第2模态波, 其特征频率约为215 kHz, 第9测点处第2模态波幅值达到最大、 特征频率约为206 kHz, 第10测点幅值开始出现衰减、 特征频率约为198 kHz. 该结果与图 10中NPLS结果吻合较好, NPLS结果中在x=300 mm(第8测点)和x=330 mm(第9测点)之间出现有“绳状”第2模态波结构, 在第10测点(x=360 mm)NPLS结果中第2模态波结构消失, 边界层进入转捩区, 但在PSD结果中, 此处仅表现为第2模态波幅值出现衰减. 同时, 根据图 12的互相关计算结果可知,x=310 mm附近的第2模态波的特征频率约为224 kHz, 该结果与PSD结果中的特征频率也相差不大.
当Re=1.75×107m-1, 第2模态波信号在第6测点开始出现; 发展到第9测点第2模态波幅值达到最大, 同时低频成分占比也有所增加, 第10测点第2模态波信号已经消失, PSD呈现为典型的湍流形态. 与尖锥PSD结果对比可见, 钝锥模型中边界层发展更加缓慢, 边界层转捩更加困难.
图 17所示为根据功率谱密度结果所得第2模态波的频率范围对脉动压力时序信号进行带通滤波所得的结果(左边)以及根据滤波后的时序信号进行互相关计算所得的结果(右边), 为将各测点分开显示, 分别对相邻测点所得的曲线在垂直方向进行偏移(压力曲线偏移量数值为0.2, 互相关结果偏移数值为1),图中每条曲线下有其对应的测点物理坐标,Tlag表示两侧点之间互相关计算得到的相对延时,R12表示相关因子(相关因子的大小反映两组数据的相关程度, 其绝对值在0到1之间,R12越接近1, 表示两个量之间的相关程度就越强, 反之,R12越接近于0, 两个量之间的相关程度就越弱). 滤波器选用Chebyshev Ⅰ型滤波器, 通带频率范围根据图 15, 16中的功率谱密度计算结果所得的第2模态波的频率范围来确定.

(a)Re=1×107 m-1

(b)Re=1.65×107 m-1
根据滤波后的时序信号, 可直接观察到各测点第2模态波波包的发展过程. 例如在图 17(a)中前5 个测点中滤波后的脉动压力曲线中波包结构均不明显, 从第6测点开始出现有明显的波包结构, 在第9测点处波包结构最为明显. 从滤波后的脉动压力时序结果中难以直接获得更多的信息, 因此对滤波后的脉动压力数据进行互相关计算.

(a) Band-pass filtering(sharp cone, Re=1×107 m-1)

(b) Cross-correlation calculation(sharp cone, Re=1×107 m-1)

(c) Band-pass filtering(sharp cone, Re=1.3×107 m-1)

(d) Cross-correlation calculation(sharp cone, Re=1.3×107 m-1)

(e) Band-pass filtering(blunt cone, Re=1.75×107 m-1)

(f) Cross-correlation calculation(blunt cone, Re=1.75×107 m-1)


为进一步观察单位Reynolds数变化对N值的影响, 采用式(1)对上述3种单位Reynolds数条件下的N值进行了计算, 结果如图 18所示.图中横坐标为PSD结果中的频率f, 纵坐标为压力测点的位置, 颜色代表的是某测点处频率f对应的N值的大小, 虚线代表N值为0.12的等高线.

表1 第2模态波平均传播速度及波长等参数计算结果

(a)Re=1×107 m-1
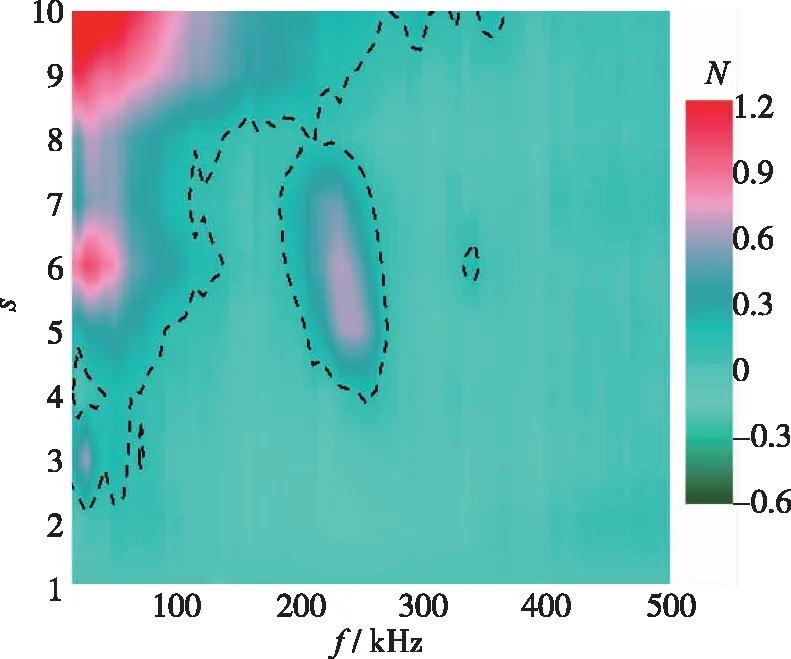
(b)Re=1.3×107 m-1

(c)Re=1.5×107 m-1图18 尖锥N值分布Fig. 18 Contours of the N factor of the sharp cone
图 18 (a)中200 kHz附近的高亮区域即为第2模态波的N值分布. 可见, 第2模态波在第9测点处N值达到最大, 第10测点则出现大幅衰减. 当增大至Re=1.3×107m-1时, 如图 18(b)所示, 低频成分的N值有所增大, 第2模态波范围往上游移动. 继续增大至Re=1.5×107m-1时, 如图 18(c)所示,N值在低频部分出现明显增大, 第2模态波的区域也大幅前移, 在第3至第5测点之间第2模态波的区域较为明显, 第6测点开始, 低频部分N值出现明显增大, 第2模态波开始消失.
图 19 所示为钝锥在Re=1.75×107m-1时不同测点在不同频率下的N值分布.图中可见, 即使在最大单位Reynolds数条件下, 前5个测点的N值均很小, 从第6测点开始, 在200~300 kHz之间出现有第2模态波对应的高亮区域, 继续往下游发展, 高亮区域逐渐向低频方向倾斜, 表明第2模态波的频率在逐渐降低. 发展到第9测点时, 第2模态波对应的高亮区域仍清晰可见, 同时低频部分的N值也出现了明显增大. 第10测点处, 第2模态波对应的高亮区域已经消失, 较大的N值主要都分布于低频部分.

图19 钝锥N值分布(Re=1.75×107 m-1)Fig. 19 Contours of the N factor of the blunt cone(Re=1.75×107 m-1)
2.3 TSP结果
为加深对圆锥边界层转捩规律的认识, 采用TSP技术对0°攻角时3种单位Reynolds数条件下的尖锥模型表面温升变化进行了测量, 所得结果如图 20 所示,图中所示温升分布是在风洞启动并达到稳定状态后计算3 s时间间隔内的平均温升.图中可见, 在单位Reynolds数较低的情况下, 圆锥表面整体温升分布较为均匀, 未出现有温升突变的区域. 当增加至Re=1.3×107m-1时, 在尖锥尾端x=334 mm附近温升突然开始增大, 表面边界层在此开始发生转捩. 继续增大至Re=1.5×107m-1, 边界层转捩阵面与图 20(b)中的较低Reynolds数相比有明显的前移, 同时单位Reynolds数增大后, 温升值也有明显增大.图 20中3种单位Reynolds数下的温升分布结果表明: 随着单位Reynolds数的增加, 尖锥边界层转捩前移, 尖锥表面气动加热也逐渐加剧.
图 21所示为0°攻角条件下钝锥模型在单位Reynolds数为Re=1.75×107m-1时的表面温升分布云图. 与图 20(c)结果相比可见, 当头部钝度增加至R=1.67 mm后, 边界层转捩明显有所推迟, 但同样可见随着单位Reynolds数的增加, 温升的绝对值有所增大.

(a)Re=1×107 m-1

(b)Re=1.3×107 m-1

(c)Re=1.5×107 m-1图20 尖锥表面温升分布云图Fig. 20 Contours of the surface temperature rise for the sharp cone

图21 钝锥表面温升分布云图(Re=1.75×107 m-1)Fig. 21 Contours of the surface temperature rise for the blunt cone(Re=1.75×107 m-1)

3 结论
通过NPLS技术和PCB传感器以及TSP技术, 在Ma=6风洞内开展了0°攻角、 不同单位Reynolds数(Re=1×107~1.75×107m-1)条件下的7°圆锥高超声速边界层转捩实验, 得到了尖锥(R<0.1 mm)和钝锥(R=1.67 mm)表面边界层在不同单位Reynolds数下的NPLS流场精细结构图像以及圆锥壁面的脉动压力分布和温升分布情况, 并采用PSD、 互相关计算和N值计算分析了边界层内扰动波的发展规律, 主要得到了以下几点结论:
(1) 得到了圆锥边界层从层流发展至出现“绳状”第2模态波, 最终发展为湍流的完整的NPLS流动显示结果; 观察到了第2模态波非常精细的结构分布; 表明在0°攻角时, 研究条件下的圆锥边界层转捩由第2模态波主导.
(2) 尖锥和钝锥边界层中第2模态波向下游发展均表现为特征频率逐渐降低、 幅值先增大后衰减; 低频成分逐渐增加.
(3) 钝锥边界层中在第2模态波消失之后、 边界层转捩为湍流之前出现波长约为第2模态波波长5倍(甚至更长)的、 特征频率约为31 kHz(或更低)的大涡结构. 表明边界层发展过程中, 第2模态波发展速度快, 但达到饱和后会逐渐衰减; 而低频模态在第2模态衰减后仍在发展, 最后模态之间的相互作用等因素使边界层完成转捩.
(4) 随单位Reynolds数增加, 尖锥和钝锥表面边界层转捩均提前, 但相同单位Reynolds数条件下, 钝锥边界层转捩更加靠后.
(5) 单位Reynolds数增加, 尖锥表面气动加热加剧.

