低维不可分解幂零Leibniz代数的局部自同构和局部导子

傅 珍, 刘文德

(海南师范大学 数学与统计学院, 海口 571158)

0 引 言

Leibniz代数[9-10]是李代数的推广. 目前, 关于Leibniz代数的研究已有很多结果, 例如Leibniz代数的分类[11-13]、 导子和自同构的刻画[14-17]等. 本文基于文献[17]中不可分解的三维幂零Leibniz代数的分类与自同构群的研究结果, 利用线性方程组理论以及矩阵技巧, 刻画复数域上不可分解的三维幂零Leibniz代数的全部局部导子与局部自同构. 结果表明, 幂零Leibniz代数具有更多的非平凡局部导子与局部自同构.

设L是域F上的一个线性空间, [,]:L×L→L是双线性映射, 若其满足Leibniz等式：

[x,[y,z]]=[[x,y],z]-[[x,z],y], ∀x,y,z∈L,

则称L是Leibniz代数. 对Leibniz代数L, 令L1=L,Lk+1=[Lk,L], 其中k≥1.若存在正整数k>0, 使得Lk=0, 则称L是幂零的.

1 预备知识

一般地, 如果一个代数不能表示为其理想的直和, 则称其为不可分解的.复数域上三维不可分解的幂零Leibniz代数分类如下：

引理1[14]在同构意义下, 不可分解的三维幂零Leibniz代数可分为N1,N2(α),N3,N4, 其非平凡乘法表分别为：

1)N1: [e1,e1]=e2, [e2,e1]=e3;

2)N2(α): [e2,e1]=e3, [e1,e2]=αe3;

3)N3: [e1,e2]=e3, [e2,e1]=-e3;

4)N4: [e1,e1]=e3, [e2,e1]=e3, [e1,e2]=-e3.

这里{e1,e2,e3}是该代数的一组基,α是非零复数且满足α≠±1.

引理2[17]设φ为Leibniz代数L的可逆线性变换, 则下列结论成立:

1) 当L=N2(α)时,φ是L的自同构当且仅当φ具有形式

这里a11a22≠0；

2) 当L=N3时,φ是L的自同构当且仅当φ具有形式

这里a11a22-a12a21≠0；

3) 当L=N4时,φ是L的自同构当且仅当φ具有形式

这里a11≠0.

文献[17]给出了N2(α),N3,N4的自同构, 下面本文给出N1的自同构.由N1的乘法及自同构定义, 易得：

命题1设φ为N1的可逆线性变换, 则φ是N1的自同构当且仅当φ具有形式

这里a11≠0.

上面讨论了不可分解的三维幂零Leibniz代数L的自同构, 下面讨论其局部自同构.本文总设T是L的一个线性变换, 其在标准基下的矩阵为T=(tij)3×3, 其中tij∈,i,j=1,2,3.

2 主要结果

定理1设T是Leibniz代数L的一个线性变换, 则下列结论成立:

1) 当L=N2(α)时,T是L的局部自同构的必要条件为T具有形式

(1)

这里t11t22t33≠0；

2) 当L=N3时,T是L的局部自同构的必要条件为T具有形式

(2)

这里t33≠0,t11t22-t12t21≠0；

3) 当L=N4时,T是L的局部自同构的必要条件为T具有形式

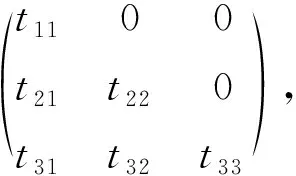
(3)

这里t11t22t33≠0；

4) 当L=N1时,T是L的局部自同构的必要条件为T具有形式(3), 这里t11t22t33≠0.

证明： 只需证明1), 类似可证2),3),4).

设T是N2(α)的局部自同构, 则对任意的x∈N2(α), 存在φx∈Aut(N2(α)), 使得T(x)=φx(x).于是, 分别取x=(1,0,0)T,(0,1,0)T,(0,0,1)T, 可得T的形式为式(1), 其中t11t22t33≠0.证毕.

定理1表明, 任意不可分解的三维幂零Leibniz代数均具有不是自同构的局部自同构.

下面刻画三维幂零Leibniz代数L=N1,N2(α),N3,N4的局部导子.设D是L的一个线性变换, 其在标准基下的矩阵为D=(dij)3×3, 其中dij∈,i,j=1,2,3.

定理2设D是Leibniz代数L的一个线性变换, 则下列结论成立:

1) 当L=N1时,D是L的导子当且仅当D具有形式

(4)

2) 当L=N2(α)时,D是L的导子当且仅当D具有形式

(5)

3) 当L=N3时,D是L的导子当且仅当D具有形式

(6)

4) 当L=N4时,D是L的导子当且仅当D具有形式

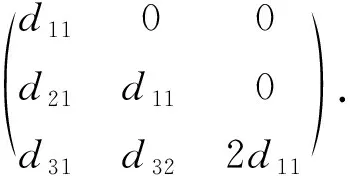
(7)

证明: 只需证明1), 类似可证2),3),4).

充分性.对任意的x,y∈N1, 令

则

故

于是

而

从而

因此D[x,y]=[D(x),y]+[x,D(y)], 即D是N1的导子.

必要性.设D∈Der(N1), 则对任意x,y∈N1, 由N1的乘法运算及导子定义可得D具有形式(4).证毕.

上面得到了N1,N2(α),N3,N4四种不可分解的三维幂零Leibniz代数的导子, 下面讨论其局部导子.设Δ是Leibniz代数L的一个线性变换, 其在标准基下的矩阵为Δ=(δij)3×3, 其中δij∈,i,j=1,2,3.

定理3下列结论成立:

1) 当L=N1时,Δ是L的局部导子当且仅当Δ具有形式

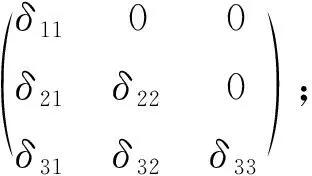
(8)

2) 当L=N2(α)时,Δ是L的局部导子当且仅当Δ具有形式

(9)

3) 当L=N3时,Δ是L的局部导子当且仅当Δ具有形式

4) 当L=N4时,Δ是L的局部导子当且仅当Δ具有形式(8).

证明: 只需证明1), 类似可证2),3),4).

必要性.设Δ是N1的局部导子, 则对任意的x∈N1, 存在Dx∈Der(N1), 使得Δ(x)=Dx(x).分别取x=(1,0,0)T,(0,1,0)T,(0,0,1)T, 经计算可知Δ具有形式(8), 这里δ11δ22δ33≠0.

充分性.设Δ具有形式(8), 要证Δ是N1的局部导子, 即证对任意的x=(x1,x2,x3)T∈N1, 存在Dx∈Der(N1), 使得Δ(x1,x2,x3)T=Dx(x1,x2,x3)T.

当Δ(x1,x2,x3)T=Dx(x1,x2,x3)T时, 有

即

(10)

其中a,b,c为未知量.方程组(10)的增广矩阵为

易证：

① 当x1=x2=x3=0时, 系数矩阵与增广矩阵的秩均为0;

② 当x1=0,x2=0,x3≠0时, 系数矩阵与增广矩阵的秩均为1;

③ 当x1=0,x2≠0时, 系数矩阵与增广矩阵的秩均为2;

④ 当x1≠0时, 系数矩阵与增广矩阵的秩均为3.

根据线性方程组理论, 方程组(10)有解, 因此Δ是N1的局部导子. 证毕.

定理3表明, 任意不可分解的三维幂零Leibniz代数均具有不是导子的局部导子.