周期性负荷扰动下电网及弹簧网强迫功率振荡分析

程志勇，路广才，竺炜

(长沙理工大学 电气与信息工程学院，长沙 410114)

0 引 言

随着我国电网规模不断扩大，低频振荡已成为影响互联电网安全稳定运行的突出问题、低频振荡事故时有发生[1-4]。目前有关电力系统低频振荡研究较为成熟的理论主要有负阻尼理论及强迫功率振荡理论[5-8]，前者由于系统本身缺乏足够的阻尼，尤其是随着大容量机组高放大倍数、快速励磁系统的比例增加，系统阻尼进一步下降，甚至变为负阻尼，当系统受到外部扰动时，就会产生发电机转子间的相对摇摆，表现在输电线路上即出现功率波动[9]。后者主要是由于系统中存在持续周期性小扰动，当扰动频率与电力系统固有振荡频率相同或接近时，就会出现强烈的共振现象[10]。针对负阻尼低频振荡，可以通过增强系统阻尼加以抑制，如加强电网结构、采用直流输电技术、输电线路采用串联补偿电容、加装静止无功补偿器(Static Var Compensator, SVC)、附加电力系统稳定器(Power System Stabilizer, PSS)等[11-12]。而对于强迫功率振荡，由于振荡源的不确定性，振荡事故难以提前预测，因此对其深入研究具有重要实际意义。文献[13-14]分别从单机和多机系统阐述了强迫功率振荡产生的机理。文献[15]分析了汽轮机压力脉动对强迫功率振荡的影响。文献[16]通过对汽轮机组功频调速控制机制的研究，分析了电网侧扰动对共振型低频振荡的影响。文献[17]从负荷角度出发，指出周期性负荷引发强迫功率振荡的机理。文献[18]基于功率谱密度方法搭建了多机系统的频率响应模型，分析了随机扰动下电力系统的强迫功率振荡特征。

文章通过将电网映射成弹簧网，研究了负荷扰动下强迫功率振荡的特征，利用电网与弹簧网振荡模态的对比分析，验证了弹簧网的合理性，为更好的研究强迫功率振荡提供一种新的思路。

1 单机无穷大系统及单自由度弹性系统

1.1 单机无穷大系统分析

图1 单机无穷大系统Fig.1 A single-machine infinite-bus system

忽略线路损耗及分布电容，单机无穷大系统线性化后的运动方程可表示为：

(1)

式中ΔPe=KΔδ，K=E′U/X∑cosδ0为同步力矩系数，M为发电机惯性时间常数，D为阻尼系数，Δδ为功角偏差。

忽略原动机功率变化，即令ΔPm=0，则式(1)又可以表示为：

(2)

特征方程为：

(3)

无阻尼时，系统固有振荡频率为：

(4)

设节点2处存在负荷波动，则有

ΔPe=KsΔδ+KpΔPd+KqΔQd

(5)

式中Ks与K类似，视为同步力矩系数，Kp、Kq为与负荷相关的系数[17]，ΔPd，ΔQd为负荷波动量。

若仅考虑有功负荷变化，即ΔQd=0，且满足ΔPd=ΔPdmsin(ωt)，并将式(5)带入式(1)后整理得：

(6)

上式为二阶常系数非齐次微分方程，其解由通解(自由振荡)和特解(强迫振荡)构成[13]。设特解为Δδ=Bsin(ωt-φ)，将其代入式(6)可解得强迫功率振荡振幅及相位：

(7)

(8)

式中υ=ω/ωn为频率比，ζ=D/(2Mωn)为系统阻尼比。由式(7)可知，当频率比υ=1，即扰动频率接近或等于系统固有频率时，振幅最大，将会产生强迫功率振荡。

1.2 单自由度弹性系统分析

单自由度弹性系统由质量块(质点)、弹簧、阻尼器、固定点构成[19]，其结构如图2所示。

图2 单自由度弹性系统Fig.2 Single degree of freedom elastic system

无扰动时系统处于静止状态，质点位于平衡位置。以平衡点为坐标原点建立坐标轴x，则根据牛顿定律可得系统的运动微分方程：

(9)

式中m为质量，单位kg；c为阻尼系数;k为弹性系数(刚度系数)，单位N/m;p0sin(ωt)为周期性扰动。解得共振振幅与相位：

(10)

(11)

对比式(6)与式(9)，可得到如下映射关系：

文献[20]中已定义弹簧弹性系数k和弹簧位移x：

(12)

x=θj-θi

(13)

式中Ui、Uj为线路首末端电压幅值，θi、θj为其对应相位，θij为相位差，XL为线路阻抗。

2 多机电力系统及多自由度弹性系统

2.1 多机电力系统分析

发电机采用二阶模型，文献[17]表明机组电磁功率的偏移可以表示为转子角偏移和负荷扰动的函数，即：

(14)

式中i=1，2，…，n为对应发电机台数，Kij=∂Pei/∂δj为等效同步系数，Kpi为负荷有功功率机组分配因子，ΔPL为负荷扰动。

多机系统线性化后的运动方程为：

(15)

忽略原动机机械功率变化，由式(14)、式(15)，整理后得到一个由多机系统构成的常系数非齐次微分方程组：

(16)

针对小扰动下的电力系统低频振荡问题，通常是将线性化后的运动方程表示成状态方程形式，然后利用状态方程系数矩阵获取系统振荡模态信息，并求解状态变量[21]。故式(16)又可以改写成状态方程矩阵形式：

(17)

(18)

(19)

式(19)右边第一项为系统自由振荡项，与状态变量的初值有关；第二项为强迫振荡项，与扰动向量有关。由于阻尼的存在，系统自由振荡项最终衰减为零。若扰动一直持续下去，则强迫振荡项不随时间衰减，表现为持续性的周期振荡，只有当扰动源消失，强迫振荡才逐渐衰减至初始状态，所以相比自由振荡而言，强迫振荡更值得关注。

设矩阵A有n个线性无关的特征向量，则有：

eAt=ΦeΛtΦ-1

(20)

式中Λ为矩阵A的特征值λi构成的对角矩阵;Φ为矩阵A特征值对应的特征向量;Φ-1为Φ的逆矩阵。电力系统中的负荷波动可以利用傅里叶变换将其分解成一系列的周期性函数组合，即可设扰动满足：

B(t)=Bsin(ωt)

(21)

式中B=[B1B2…Bn]T，则由式(19)、式(20)及式(21)可解得强迫振荡项：

xF(t)=ΦUi(ωt)Φ-1B

(22)

式中

(23)

(24)

式中σi和ωi为特征值λi所对应的实部和虚部。由式(24)可以看出当扰动频率满足ω=ωi时，ui(ωt)幅值最大，系统发生第i阶强迫振荡。

2.2 多自由度弹性系统分析

将电网模型映射成弹簧网模型，并在弹簧网模型中增加原发电机内电势支路对应节点，编号1，2，…，n；其余网络节点编号n+1，n+2，…，n+m。如图3所示，节点i，j受力分别为fi、fj，位移为xi、xj。类似于求解潮流过程中各节点注入有功功率增量：ΔP=(UiUj/XL)cosθijΔθij，弹簧网中各节点受力满足：

图3 弹性支路受力示意图Fig.3 Strength schematic diagram of elastic branch

Δfi=fj-fi=k(xj-xi)=kΔxi

(25)

式中i=1，2，…，n+m。

将式(25)改写成矩阵形式

(26)

(27)

将式(27)带入到弹簧网质量块运动方程可得：

(28)

式中i=1，2，…，n。对比式(16)与式(28)，发现二者在数学形式上具有一致性，采用类似求解式(16)的方法，以弹簧位移及位移导数为状态变量，将式(28)改写成状态方程矩阵形式，通过求解状态方程所对应的系数矩阵即可得到系统的振荡模态等信息，同样得出在扰动频率与系统固有频率相同时发生强迫振荡，具体求解过程同上，这里不再详述。

3 算例分析

3.1 单机无穷大系统及单自由度弹性系统

设2号母线处发生有功负荷周期性扰动，扰动频率等于系统有阻尼固有振荡频率ωd，扰动大小为总有功负荷10%。即：ΔPd=0.03sin(7.80t)，扰动时间0～10 s。发电机有功出力曲线如图4所示。

图4 单机无穷大系统发电机有功出力曲线Fig.4 Generator active output curve of single-machine infinite-bus system

单自由度弹性系统结构如图5所示，由式(12)、式(13)，可得发电机支路、变压器支路、线路弹性系数分别为：KM=3.570，KT=49.764，KL=3.280;质量块：m=M/ω0=0.025 5;阻尼系数：c=D/ω0=0.019 1。

图5 单自由度弹性系统模型Fig.5 Single degree of freedom elastic system model

弹性系统振荡模式：γ1，2=-0.375±8.050i，阻尼比：ζ=4.653，无阻尼振荡频率ωn=1.282 Hz，有阻尼振荡频率ωd=1.280 Hz。

施加如图5所示扰动，扰动大小：ΔfL=0.03sin(8.05t)，扰动时间0～10s，质量块所受拉力如图6所示。

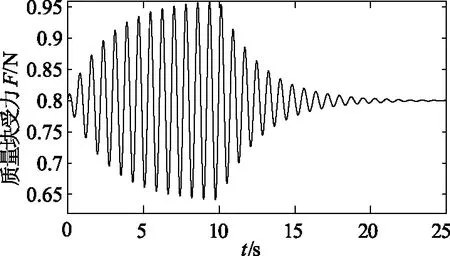
图6 单自由度系统质块受力曲线Fig.6 Mass stress curve of single degree of freedom system

3.2 多机电力系统及多自由度弹性系统

多机电力系统采用IEEE 4机2区模型，发电机采用二阶模型。阻尼系数D=6 s，详细参数见文献[22]，计算过程中均已将各自额定容量下的参数折算到100 MW系统基准容量下。系统结构如图7所示。

图7 4机2区系统Fig.7 Four-machine two-area system

对图7所示系统进行小干扰稳定分析，PSASP计算结果如表1所示。该系统具有3个机电振荡模式，以模式1为例，在负荷Load_1处施加正弦扰动：ΔPL1=0.05sin(6.62t)，扰动时间0～10 s，诱发系统产生强迫功率振荡，振荡结果如图8所示。

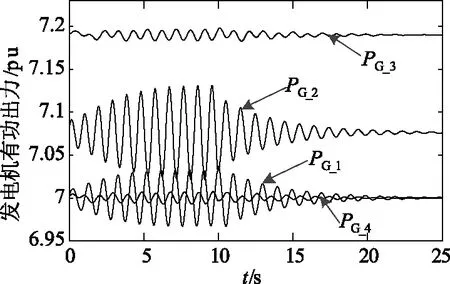
图8 四机两区系统发电机出力曲线Fig.8 Generator active output curve of four-machine two-zone system

图9 4机2区弹性系统模型Fig.9 Four-machine two-area elastic system model

图10 四机两区弹性系统质块受力曲线Fig.10 Mass stress curve of four-machine two-zone elastic system

从表1、表3可以看出，多机系统电网振荡模式与映射弹簧网振荡模式具有一致性，二者无论振荡频率还是衰减阻尼比均十分接近。以模式1为例，电网与弹簧网振荡频率均在1 Hz以上，满足局部振荡对应频率1～2 Hz范围，从图8中可以看出，1、2号发电机组功率振荡较大，3、4号机组功率振荡较小，符合局部振荡特征。图10中，1、2号质量块受力振荡幅值显著大于3、4号质量块受力，同样表现为局部振荡特征，二者振荡模式相对应。

表1 4机2区系统小干扰稳定结果Tab.1 Result of small signal stability of four-machine two-area system

表2 弹簧网各支路弹性系数Tab.2 Elasticity coefficient of spring network branches

表3 4机2区弹性系统线性化结果Tab.3 Linearization result of four-machine two-area elastic system

以上算例表明，无论是单机无穷大系统与单自由度弹性系统，还是多机系统和多自由度弹性系统，映射后的弹性系统模型均能较为准确的反映原电网的振荡模式。

4 结束语

周期性负荷扰动能够诱发系统振荡，机组数量增多，系统振荡模式随之增加，当负荷扰动频率接近或等于某一系统固有振荡频率时，将会导致系统中某些机组产生强烈的功率波动。文中从理论上分析了电网与弹簧网之间的映射关系，提出了一种由弹簧网求解系统振荡模态的方法，从力学角度解释了电力系统中强迫功率振荡现象。由于弹性系数矩阵易形成的特点，利用弹簧网，仅需要知道系统的电压及相角即可得到由弹性系数构成的系数矩阵，从而得到关于整个系统的振荡模态信息，相比用电网模型更加简便实用。仿真算例进一步验证了弹簧网模型与电网模型具有一致性。该方法为研究低频振荡提供了一种新的思路，具有一定的参考价值。