含常数激励非对称Duffing系统的主共振响应及鞍结分岔研究
罗 钢,侯 磊,任双兴,陈予恕
(哈尔滨工业大学航天学院,黑龙江哈尔滨 150001)
1 概述
在非线性振动系统中,常数激励[1-2]是导致非对称性的主要因素之一,例如,在旋转机械中,裂纹转子系统受重力作用[3-4]、轴承转子系统受径向载荷作用[5-7]、基础运动及机动飞行转子系统承受惯性载荷[8-11]等。非对称性使得非线性振动系统的动力学特性相比于一般的对称系统更加复杂,尤其是在非对称因素十分显著的情况下。
Carnegie 等[12]研究了重力对Duffing 系统2 次超谐共振的影响,表明重力使得恢复力产生不对称性,势能函数的幂律指数由奇数特征变为偶数特征。
含常数激励非对称Duffing 方程的一般形式如下:
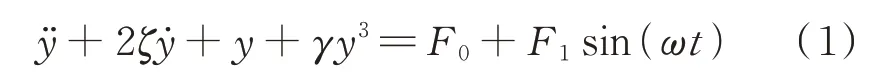
Hayashi[13]研究了参数取γ=ω=1 的情况,表明在一定参数条件下,当常数激励F0在某一范围内取值时,系统最多有5 个稳态解,能够产生多次跳跃现象。
对于带有平方非线性项的Helmholtz-Duffing方程:
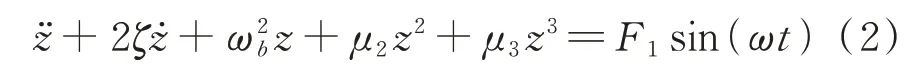
Ravindra 等[14]通过平移变换将其转化为方程(1),通过解析求解表明平方非线性的存在使得具有硬特性的Duffing 系统产生刚度增强效应,使其幅频曲线峰值点发生右移。Benedettini 等[15-17]系统研究了振动方程形如式(2)的悬索主共振响应、2 次和3 次超谐共振响应,以及1/2 次和1/3 次亚谐共振响应,表明这些共振响应中均存在软硬特性变化和多值现象,并且由于平方非线性项的存在,2 次超谐共振显著强于3 次超谐共振,1/2 次亚谐共振显著强于1/3 次亚谐共振。Murata 等[18]利用突变理论研究了方程(2)的分岔特性,阐释了跳跃现象及滞后现象的发生机制。Yagasaki[19-20]分别针对原子显微镜的尖端部分——微型悬臂梁和受线性反馈控制的单摆建立了形如方程(2)的动力学方程,利用二阶平均法分析了主共振响应的分岔性质,并给出产生亚临界鞍结分岔及超临界鞍结分岔时的激励幅值[21],还采用一种推广的亚谐Melnikov 方法研究了方程中出现的退化共振行为,表明退化共振一般会导致尖点分岔[22-23]。TIAN 等[24-25]发现在常数激励作用下,光滑非连续振子的混沌吸引子与SD 振子有显著区别。Kovacic 等[26-28]将一个准零刚度非线性隔振器模型的振动用方程(1)描述,对其主共振响应进行了细致的研究,表明在常数激励的作用下,系统能够表现出4 种不同的幅频曲线类型,除了近似线性的单解类型和具有3 个稳态解的单弯曲类型,还存在具有3 个稳态解的双弯曲类型以及具有5 个稳态解的双弯曲类型。侯磊等[29]对方程(1)描述的非对称Duffing 系统的骨架曲线和幅频响应进行了研究,发现骨架曲线的形态表现为先向左微偏后转为向右弯曲,对应的幅频曲线在简谐激励幅值较小时表现为软特性,当简谐激励幅值增大时表现出软硬特性共存现象。此外,通过奇异性分析给出了该系统在常数激励与简谐激励幅值不同组合下的6 种分岔模式[30]。
本文以形如方程(1)的含常数激励的非对称Duffing 系统为研究对象,求解强非线性Duffing 方程在常数激励与简谐激励联合作用下的主共振响应,重点研究常数激励对系统鞍结分岔的影响规律。
2 主共振响应的近似解析求解与稳定性分析
2.1 谐波平衡法求解主共振响应
采用谐波平衡法求解方程(1)的主共振响应。由于方程(1)中存在常数激励F0,其振动响应中会产生直流分量,其一阶近似解具有如下形式:

式中A0为直流分量,A1为谐波响应的幅值,θ为初相位。
将式(3)代入式(1),令常数项、余弦项和正弦项系数分别为零,可得幅频响应方程组:
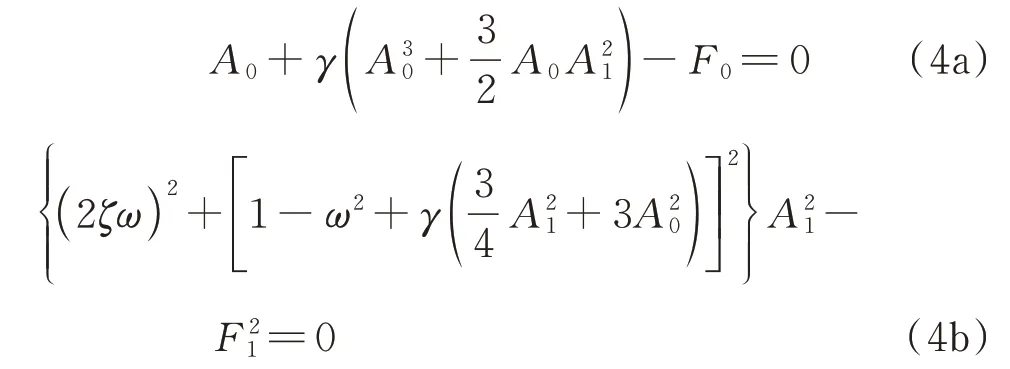
根据式(4a),A1与A0有如下关系:
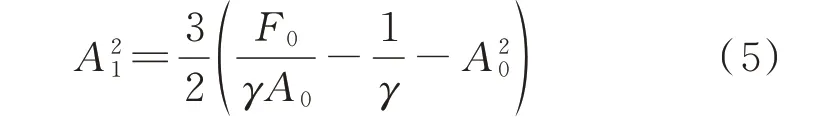
将式(5)代入式(4b),可得关于A0的方程:

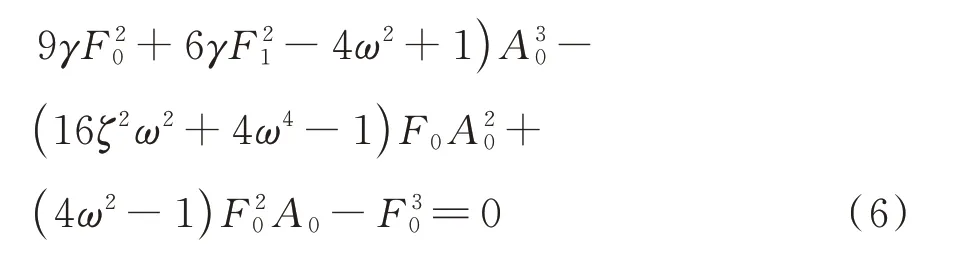
可见式(6)是关于A0的9 次方程。
根据笛卡尔符号法则,一元多项式方程具有正数解的个数要么等于其系数符号改变次数,要么比此次数小一个偶数。式(6)系数符号改变次数为5次,其具有正数解的数目为5 或3 或1,因而式(1)的主共振响应最多有5 个。
2.2 稳定性分析
采用Floquet 理论分析周期解的稳定性。在式(3)的基础上增加一个小扰动u形成的扰动解如下:
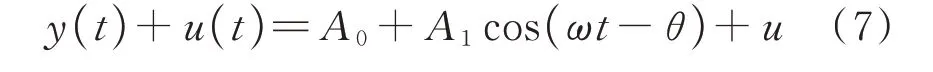
将式(7)代入式(1),注意到y也是式(1)的解,可得基于解y的线性变分方程如下:

其中:
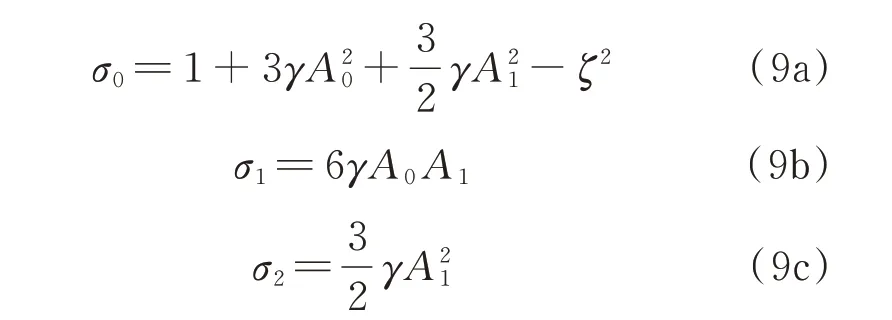
对式(8)作如下变换:
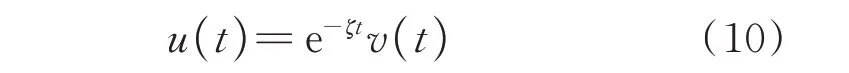
得到如下形式的Hill 方程:

根据Hill 方程的相关理论,当激励频率与规范化固有频率具有如下关系:

时,式(11)所代表的参激系统将在第n个不稳定区域发生共振。为了考察形如式(3)的解的稳定性,本文考虑第二个不稳定区域。可设式(11)的解的形式为:
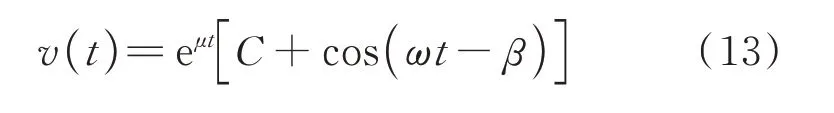
式中μ为Floquet 特征指数,其实部符号决定式(11)零解的稳定性。
仍采用谐波平衡法,取一阶近似,令常数项、余弦项和正弦项系数为零,得到如下方程组:
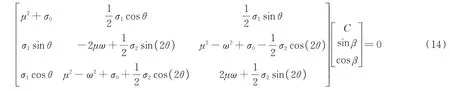
由于式(13)为非零解,则有:
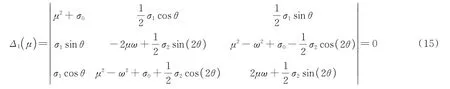
由Floquet 理论可知,方程(1)形如式(3)的周期解的稳定条件为-ζ±μ的实部小于零,又由于阻尼系数ζ>0 且μ为实数或虚数,则稳定条件等价于ζ2>μ2。结合式(15),可知稳定条件为Δ1(ζ)>0,稳定边界为Δ1(ζ)=0,其中:
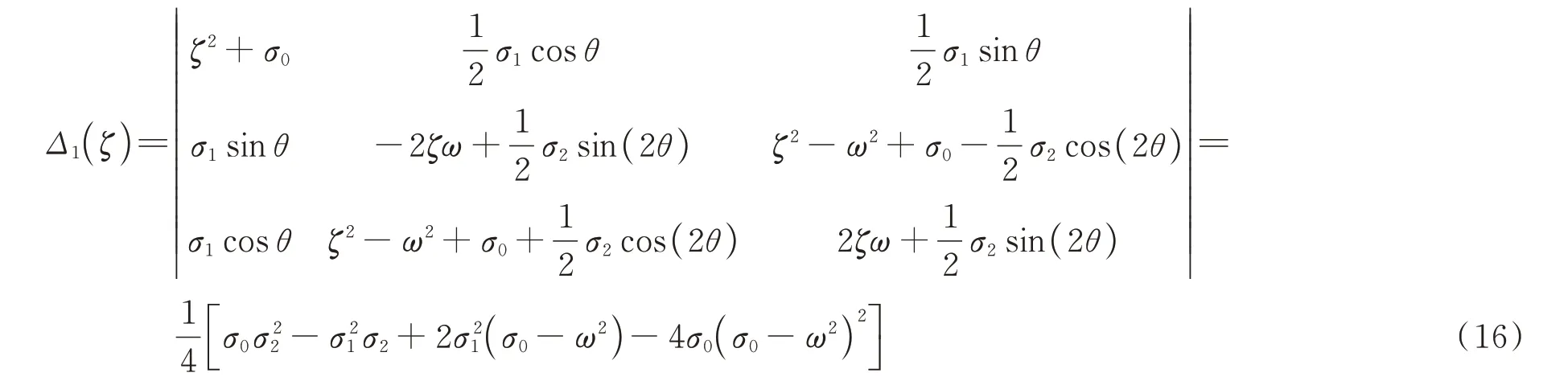
将式(9)代入式(16)并整理,得稳定边界:
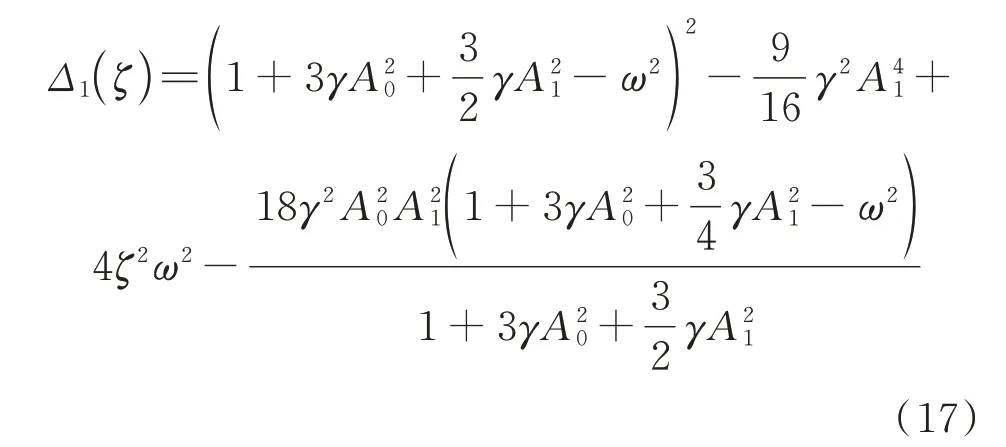
为了将周期解的稳定性反映到幅频响应曲线上,将幅频响应方程重新符号化如下:
传说,对着树洞讲出你的心事,心情会释然。找到你的树洞,埋藏进所有的眼泪和哭声,让我为你守望。不知不觉中你就会长大。

将式(18)关于频率ω求全导数,并从中解出未知数∂A0/∂ω,∂A1/∂ω和∂θ/∂ω,得:
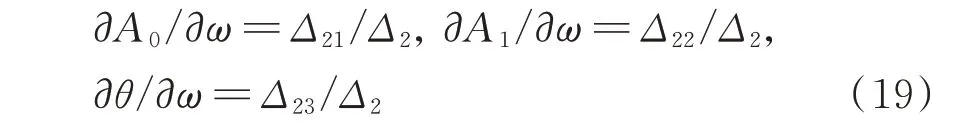
其中:
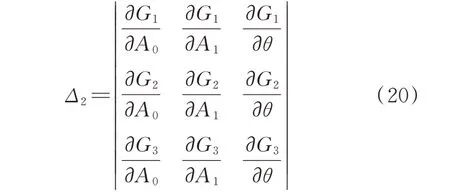
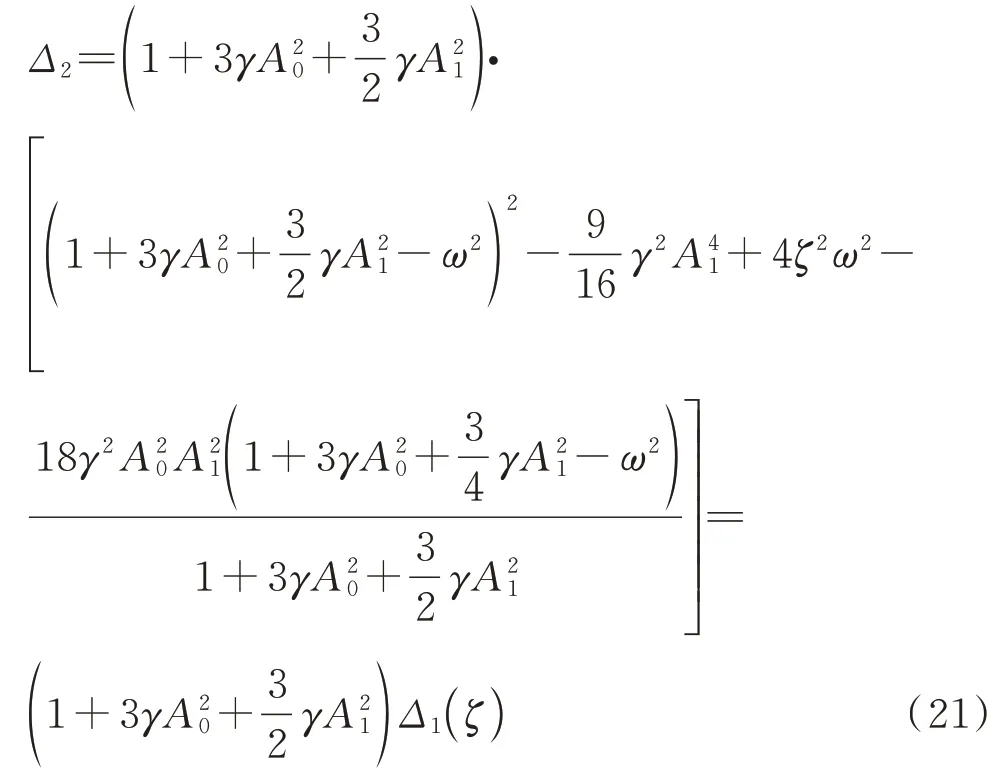
Δ2i(i=1,2,3)是用∂G1/∂ω,∂G2/∂ω和∂G3/∂ω的相关项替换行列式Δ2中第i列得到的新行列式。计算行列式Δ2并整理,得到:
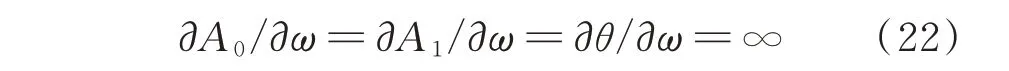
因此,当Δ1(ζ)=0 时,Δ2=0。结合式(19),在稳定边界上有:也就是说,在幅频响应曲线上,在稳定边界点处的切线斜率为无穷大,即垂直于频率轴。稳定边界将稳定解所在区域与不稳定解所在区域分隔开,可以通过式(17)来判断特定解的稳定性。
3 主共振响应中的非线性振动特性分析
3.1 主共振下的幅频响应
以系统参数取ζ=0.015,γ=4,F1=0.05 为例,在常数激励作用下,方程(1)主共振下的幅频响应曲线会出现软特性共振滞后区,随着常数激励的增大,软特性共振滞后区不断扩大,而原有的硬特性共振滞后区逐渐收缩直到完全消失,在这个演化过程中系统会表现出6 种类型的幅频响应曲线,这在文献[30]中有详细论述。本文以F0=0.8 为例,给出系统最典型的具有5 解共存情况的幅频响应曲线,如图1所示,其中实线代表稳定解,虚线代表不稳定解,箭头标示了正反向扫频时幅值的变化方向及跳跃现象。由图1 可见,随着简谐激励频率ω的增大,幅频响应曲线先向左弯曲,后向右弯曲,形成一个软特性共振滞后区和一个硬特性共振滞后区,且两个共振滞后区有一部分重合区域,在重合区域内特定ω下系统有5 个周期解,其中3 个为稳定解,2个为不稳定解,而在两个共振滞后区的非重合区域,特定ω下系统有3 个周期解,其中2 个为稳定解,1个为不稳定解。
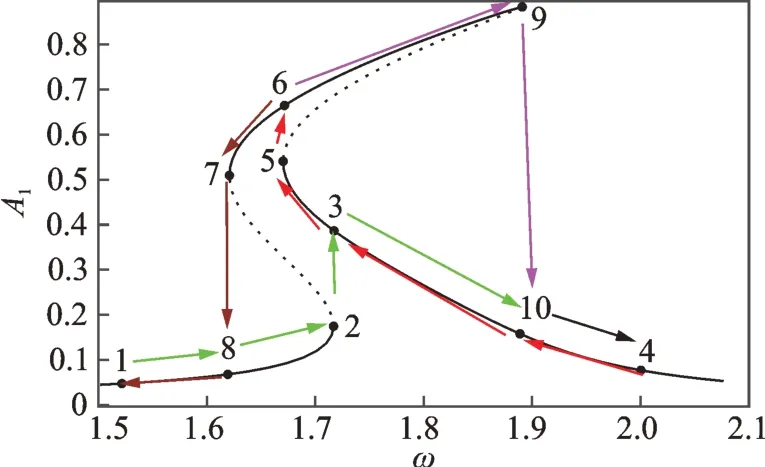
图1 F0=0.8 时系统的幅频响应曲线(ζ=0.015,γ=4,F1=0.05)Fig.1 Amplitude-frequency response when F0=0.8(ζ=0.015,γ=4,F1=0.05)
此外,图1所示系统还存在复杂的跳跃现象。从点1 出发正向扫频时,随着简谐激励频率ω的缓慢提高,系统振幅逐渐增大,经过点2 时振幅将跳跃到点3,此时若继续提高ω,则振幅逐渐减小,直到点4。从点4 出发反向扫频时,随着ω的缓慢降低,系统振幅逐渐增大,经过点3 时不发生跳跃现象,而是振幅继续逐渐增大,直到经过点5 时发生跳跃现象,系统振幅将跳跃到点6,此时若继续降低ω,则系统振幅逐渐减小,直到点7 再次发生跳跃现象,系统振幅将跳跃到点8,随着ω的进一步降低,系统振幅逐渐减小,回到点1。当系统振幅达到点6 时,若缓慢提高ω,则系统振幅会逐渐增大,直到点9 发生跳跃现象,系统振幅跳跃到点10。以ω=1.71 为例,此时系统为典型的5 解共存,通过四阶龙格-库塔法对系统求稳定解,得到系统在不同初始条件下的相图和时间历程曲线如图2所示。
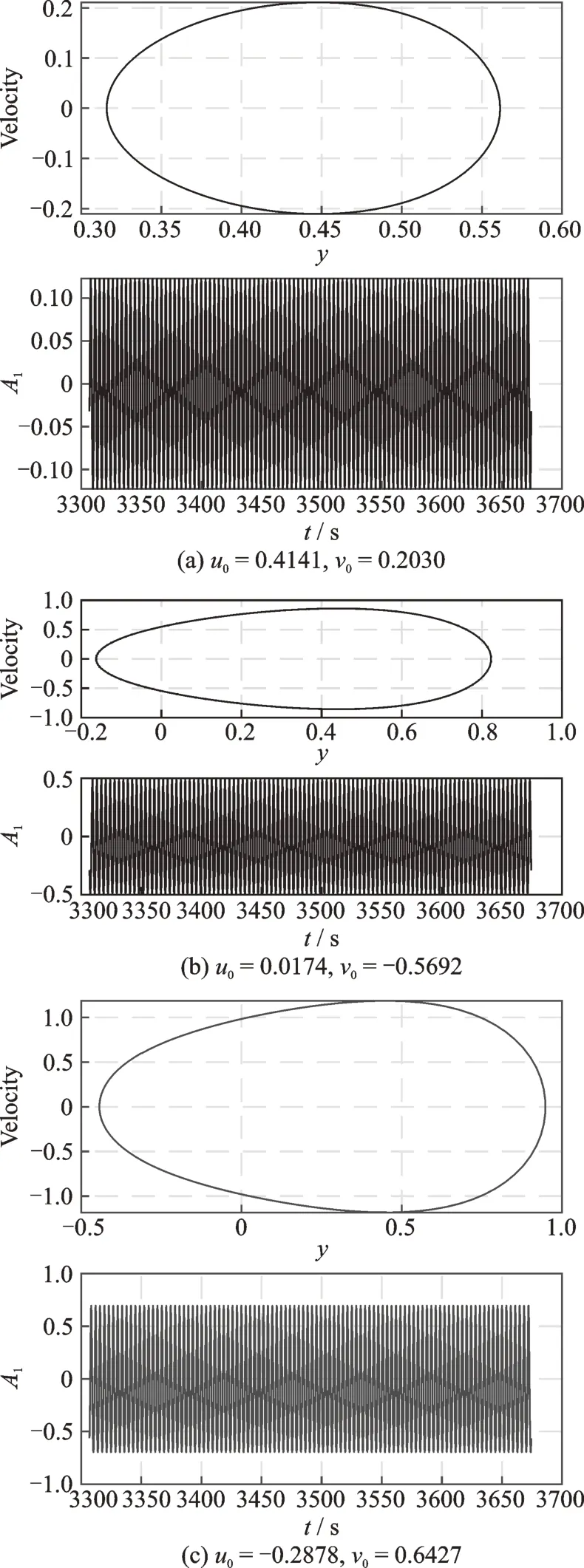
图2 ω=1.71 时系统的相图与时间历程(ζ=0.015,γ=4,F0=0.8,F1=0.05)Fig.2 Phase diagrams and time histories when ω=1.71(ζ=0.015,γ=4,F0=0.8,F1=0.05)
Duffing 系统主共振下幅频响应曲线上的跳跃点均是鞍结分岔点,软特性共振滞后区和硬特性共振滞后区的左右边界分别对应一个鞍结分岔点,即图1 中的点2、点5、点7、点9 四个点。因此,研究系统的鞍结分岔特性有助于认识其复杂跳跃现象的机理。
3.2 鞍结分岔特性分析
鞍结分岔,也称切线分岔或折叠分岔,是非线性动力学中最为基本的局部分岔模式之一,在分岔图中分岔点处的切线铅直是其典型的几何特征,利用该特征可通过幅频响应方程计算系统的鞍结分岔集,并据此对幅频响应曲线进行分类。关于分岔分析更为详细的方法,可参考文献[31]。
图3所示为系统参数取ζ=0.015,γ=4,F1=0.05 时,ω-F0平面上的鞍结分岔集。可见,鞍结分岔集由曲线ABC 和曲线FGH 组成,其中曲线ABC 为软特性共振滞后区对应的鞍结分岔集,曲线FGH 为硬特性共振滞后区对应的鞍结分岔集。图中还在每段分岔集曲线左右标示出了经过相应分岔点时系统周期解数目的变化情况,因此通过分析这些分岔集曲线可以掌握系统周期解数目增加或减少的具体情况。
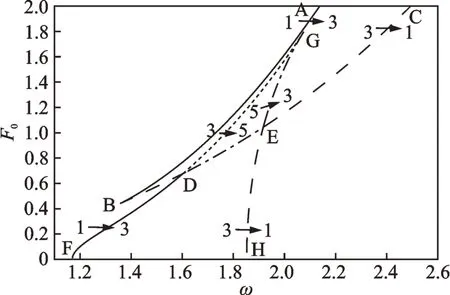
图3 ω-F0 平面上的鞍结分岔集Fig.3 Saddle-node bifurcation set on the ω-F0 plane
若以简谐激励频率ω为分岔参数,则随着ω的增大,当经过曲线AB 和DF 时,系统周期解的个数由1 个变为3 个,增加1 个稳定解和1 个不稳定解,此时系统共有2 个稳定解和1 个不稳定解。随着ω的进一步增大,当经过曲线BD,CE 和EH 时,增加的2个周期解消失,系统周期解的个数由3 个变回1 个。
在鞍结分岔集曲线ABC 和曲线FGH 的交叉区域,随着ω的增大,当经过曲线DG 时,系统周期解的个数由3 个变为5 个,增加1 个稳定解和1 个不稳定解,此时系统共有3 个稳定解和2 个不稳定解。随着ω的进一步增大,当经过曲线DE 和EG 时,增加的2 个周期解消失,系统周期解的个数由5 个变回3 个。
因此,曲线DF,DE 和EH 围成的区域为硬特性共振滞后区,系统的幅频响应曲线有3 解,这与传统的无常数激励的Duffing系统的主共振特性一致。曲线AB,BD,DG 以及曲线CE,EG 围成的区域为软特性共振滞后区,系统的幅频响应曲线有3 个解。曲线DE,DG,EG 围成的区域为软特性共振滞后区和硬特性共振滞后区的重叠区域,系统的幅频响应曲线有5 个解。
当常数激励F0较小时,系统幅频响应曲线随着ω的增大其解的个数会经历1-3-1 的变化,此时系统仅有一个硬特性共振滞后区,与传统的无常数激励的Duffing系统的主共振特性一致。当F0的取值处于曲线BD 在纵轴的投影区域时,系统幅频响应曲线随着ω的增大其解的个数会经历1-3-1-3-1 的变化,此时系统同时具有硬特性共振滞后区和软特性共振滞后区,但两个共振滞后区处于分离状态。当F0的取值处于曲线DG 在纵轴的投影区域时,系统幅频响应曲线随着ω的增大其解的个数会经历1-3-5-3-1 的变化,此时硬特性共振滞后区与软特性共振滞后区有交叉。当F0更大时,硬特性共振滞后区消失,系统仅具有软特性共振滞后区,幅频响应曲线随着ω的增大其解的个数会经历1-3-1 的变化。
4 参数对鞍结分岔集的影响分析
4.1 阻尼的影响
图4所示为系统参数取γ=4,F1=0.05,阻尼系数ζ分别取0.01,0.015,0.03,0.04 和0.06 时,ω-F0平面上的鞍结分岔集。可见,随着阻尼系数的增大,系统的鞍结分岔集发生显著变化,软特性共振滞后区和硬特性共振滞后区均收缩变小,同时软特性共振滞后区向平面的右上方移动,硬特性共振滞后区向平面的左下方移动,两个共振滞后区的重叠区域也逐渐变小,直到两个共振滞后区完全分离;当ζ=0.06 时,软特性共振滞后区完全消失。表明阻尼的增大有利于抑制Duffing 系统的多解及振幅跳跃现象。
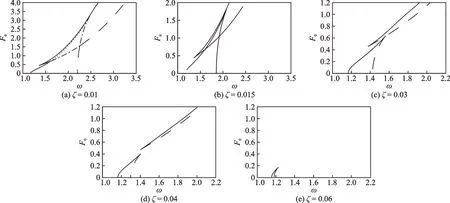
图4 不同阻尼大小下ω-F0 平面上的鞍结分岔集(γ=4,F1=0.05)Fig.4 Saddle-node bifurcation sets with different damping on the ω-F0 plane(γ=4,F1=0.05)
4.2 简谐激励幅值的影响
图5所示为系统参数取ζ=0.015,γ=4,简谐激励幅值F1分别取0.05,0.03,0.018,0.01 和0.008时,ω-F0平面上的鞍结分岔集。可见,随着简谐激励幅值的减小,系统的鞍结分岔集发生显著变化,其变化趋势与阻尼系数增大时的变化趋势相似,软特性共振滞后区和硬特性共振滞后区均收缩变小,同时硬特性共振滞后区向平面的左下方移动,但软特性共振滞后区向平面的右下方移动,两个共振滞后区的重叠区域也逐渐变小直到两个共振滞后区完全分离;当F1=0.008 时,软特性共振滞后区完全消失。结果表明简谐激励幅值的减小也有利于抑制Duffing 系统的多解及振幅跳跃现象。
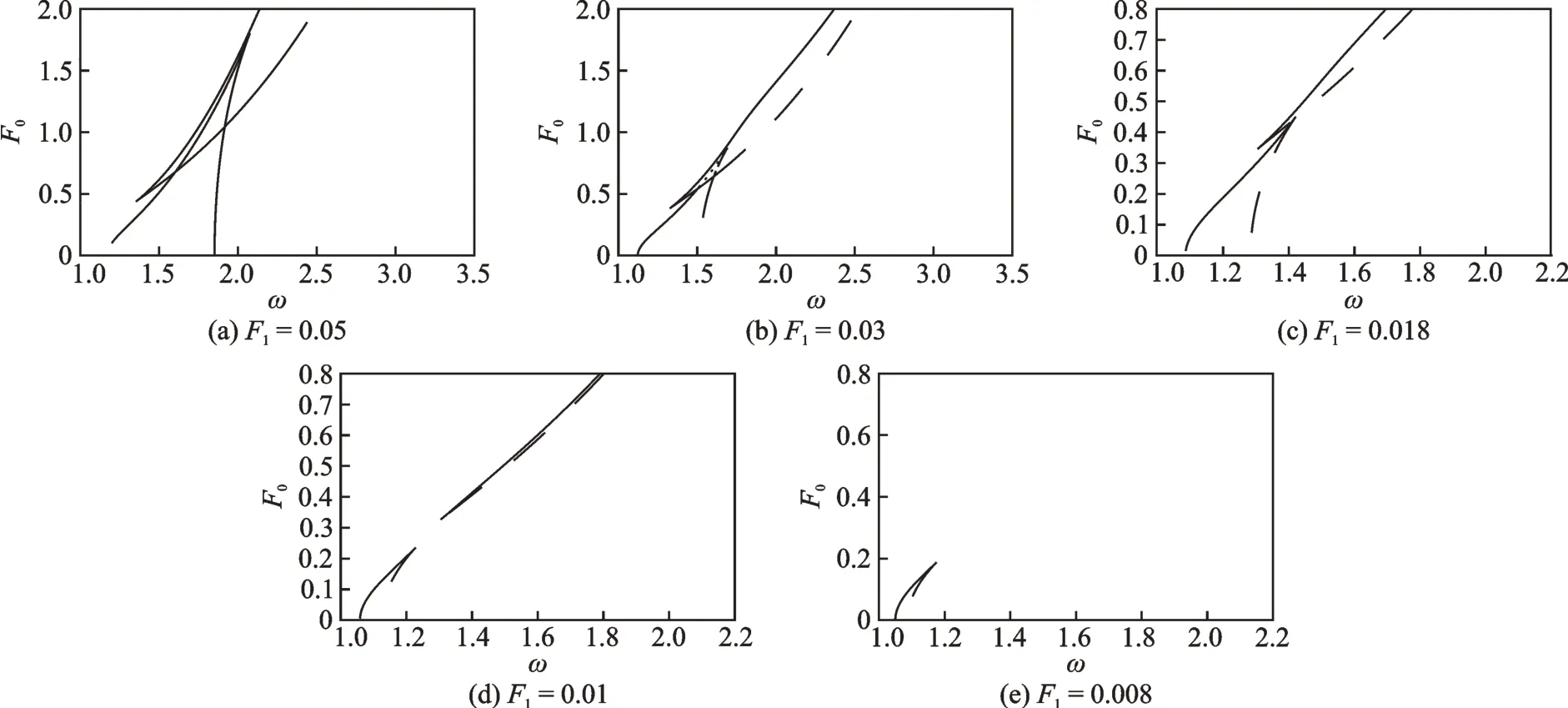
图5 不同简谐激励幅值下ω-F0 平面上的近似鞍结分岔集Fig.5 Approximate saddle-node bifurcation sets with different harmonic excitation on the ω-F0 plane
5 结论
本文针对含常数激励非对称Duffing 系统开展了鞍结分岔特性研究,采用谐波平衡法求得系统在主共振下的周期解,采用Floquet 理论分析周期解的稳定性,利用幅频响应曲线上鞍结分岔点处具有切线铅直的几何特征,计算了系统关于常数激励和简谐激励频率的鞍结分岔集,并分析了阻尼和简谐激励幅值对鞍结分岔集的影响规律,得到结论如下:
1)在特定参数条件下,系统的幅频响应曲线先向左弯曲后向右弯曲,形成一个软特性共振滞后区和一个硬特性共振滞后区,在两个共振滞后区的重合区域内,系统具有5 解共存现象,5 个周期解中3个为稳定解,2 个为不稳定解。
2)在5 解共存情况下,系统幅频响应曲线上表现出复杂的振动跳跃现象,在软特性共振滞后区和硬特性共振滞后区的左右边界上共形成4 个振动跳跃点,均为鞍结分岔点。
3)在常数激励与简谐激励频率构成的参数平面上,鞍结分岔集由两条曲线组成,其中一条为软特性共振滞后区对应的鞍结分岔集;另一条为硬特性共振滞后区对应的鞍结分岔集。两条曲线包围的参数区域为多解参数区,其中两条曲线的交叉区域为5 解共存参数区。
4)随着常数激励的增大,系统幅频响应曲线上表现出软特性逐渐增强、硬特性逐渐变弱的现象,两者对应的共振滞后区从分离到交叉,直到硬特性共振滞后区消失,其中在共振滞后区交叉的参数区存在5 解共存现象和复杂的振动跳跃现象。
5)增大系统阻尼或减小简谐激励幅值,系统的鞍结分岔集发生显著变化,软特性共振滞后区和硬特性共振滞后区均收缩变小,并且两个共振滞后区的重叠区域也逐渐变小直到两个共振滞后区完全分离,表明增大系统阻尼或减小简谐激励幅值有助于抑制系统主共振响应中的多解及复杂振动跳跃现象。

