弹性边界约束矩形板的振动特性分析：理论、有限元和实验

柴玉阳，杜绍君，李凤明

（哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨 150001）

引言

矩形板作为一种典型的结构，广泛应用于飞行器、船舶、海洋平台以及高速列车等结构中。为了避免矩形板结构在动态载荷作用下的不利振动影响，开展矩形板结构振动特性的理论和实验研究具有重要的实际意义。

目前很多学者针对矩形板的振动特性开展了大量的理论研究。Leissa［1］系统地研究了多种简单边界（自由、简支和固支）组合情况下矩形板的振动特性，研究发现对于6 种对边简支情况的矩形板可以获得精确的固有振动特征方程。Liew 等［2］利用瑞利-里茨法分析了不同边界条件下厚矩形板的振动特性。基于微分求积法，Li 等［3］研究了正交各向异性板的非线性振动特性。Aksu 等［4］基于有限差分法研究了中心开口矩形板的振动特性。Jin 等［5］提出了一种三维改进的傅里叶余弦级数方法，对一般边界条件下功能梯度矩形板的振动特性进行求解。王嘉伟等［6］通过构建单层和多层复合材料层合板的动态特性简化模型，计算了复合材料层合板的固有频率和振型。利用瑞利-里茨法，李国荣等［7］研究了典型边界条件下加筋矩形板的振动特性，分析了加筋位置及高度对结构固有频率的影响。马牛静等［8］研究了具有初始应力加筋板的非线性振动特性。鲍四元等［9］提出了一种各向异性矩形板和环扇形板在弹性约束下横向自由振动的通用解法。张俊等［10］利用改进的傅里叶级数作为位移容许函数，研究了多开口弹性约束矩形板的振动特性。

有关矩形板结构振动特性的实验研究也吸引着很多学者的关注。Shuyu［11］提出了一种解析方法计算自由边界矩形薄板的振动特性，并设计实验测试结构的固有频率，验证了所提解析方法的正确性。Pagani 等［12］基于理论和实验的方法研究了复合材料层合板结构的自由振动特性。考虑结构的几何大变形，Amabili［13］研究了不同边界条件下矩形薄板的非线性振动特性，并利用实验测试获得了与理论分析一致的频响曲线，验证了理论计算的有效性。付江松等［14］通过搭建四边自由矩形薄板横向振动的实验平台，获得矩形板的二维驻波实验图和固有频率，验证了所提理论模型的正确性。

基于以上分析可知，目前针对矩形板振动特性的研究多局限于自由、简支和固支等经典边界，对于弹性约束等边界条件需配置不同的位移函数，缺乏统一的分析模型。此外，由于模拟弹性边界的复杂性，鲜有针对弹性边界约束矩形板振动特性相关的实验研究。虽然有限元法可以处理弹性约束结构的振动问题，但不利于对相关参数进行系统分析。因此，本文基于瑞利-里茨法，通过Gram-Schmidt 法构造特征正交多项式表示位移函数，建立弹性边界矩形板的振动方程，求解其固有频率和振型。矩形板的弹性边界采用均布弹簧模拟，通过调节边界弹簧的刚度，弹性边界约束可以模拟自由、简支及固支等任意边界条件。基于本文所提方法获得结构的固有频率并与有限元及实验结果进行对比，验证本文理论模型的正确性。此外，设计一系列实验研究弹性-简支、弹性-固支等不同边界组合条件下矩形板的自由振动特性，详细分析调整不同边界弹簧刚度对矩形板结构振动特性的影响。

1 理论模型

1.1 弹性边界约束矩形板

图1 为弹性边界约束矩形板结构示意图。矩形板的长、宽、高分别为a，b和h。弹性边界由一系列均布弹簧模拟，其中包括三组均匀分布的平动弹簧和一组均匀分布的旋转弹簧。单位长度平动弹簧和旋转弹簧的刚度分别用ku，kv，kw和kθ来表示。沿y=0 旋转弹簧刚度为kθy0，平动弹簧刚度为kuy0，kvy0和kwy0。相似地，y=b，x=0 和x=a的均布弹簧刚度用kθyb，kuyb，kvyb，kwyb，kθx0，kux0，kvx0，kwx0，kθxa，kuxa，kvxa和kwxa来表示。

图1 弹性边界约束矩形板示意图Fig.1 Schematic diagram of the rectangular plate constrained by elastic boundary constraints

基于经典薄板理论，各向同性矩形板结构的位移场可表示为：

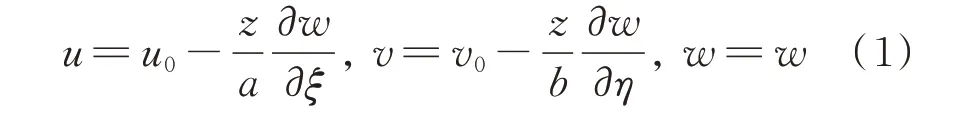
式中u和v表示结构上任一点沿x和y方向的位移；w为横向位移；u0和v0为中性层的面内位移；ξ=x/a和η=y/b为薄板无量纲的长度和宽度变量。

薄板结构的应变-位移关系式如下：

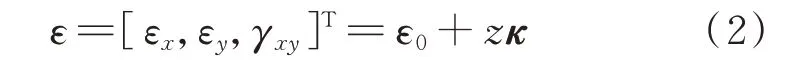
式中εx和εy为线应变；γxy为切应变；ε0为膜应变向量；κ为弯曲曲率向量，分别表示为：

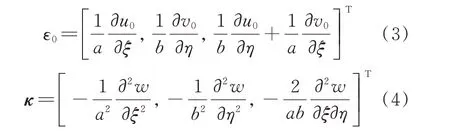
结构的本构方程可以表示为：

式中σ为与应变对应的应力；Q11=Q22=E/（1-υ2），Q12=Q21=υE/（1-υ2）和Q66=E/［2（1+υ）］为刚度系数，其中E和υ为矩形板材料的杨氏模量和泊松比。

1.2 结构系统的能量

矩形板结构的动能和势能可以表示为：

式中ρ和dV分别为矩形板的材料密度和体积元。

弹性边界ξ=0 和1 时的势能可以写为：

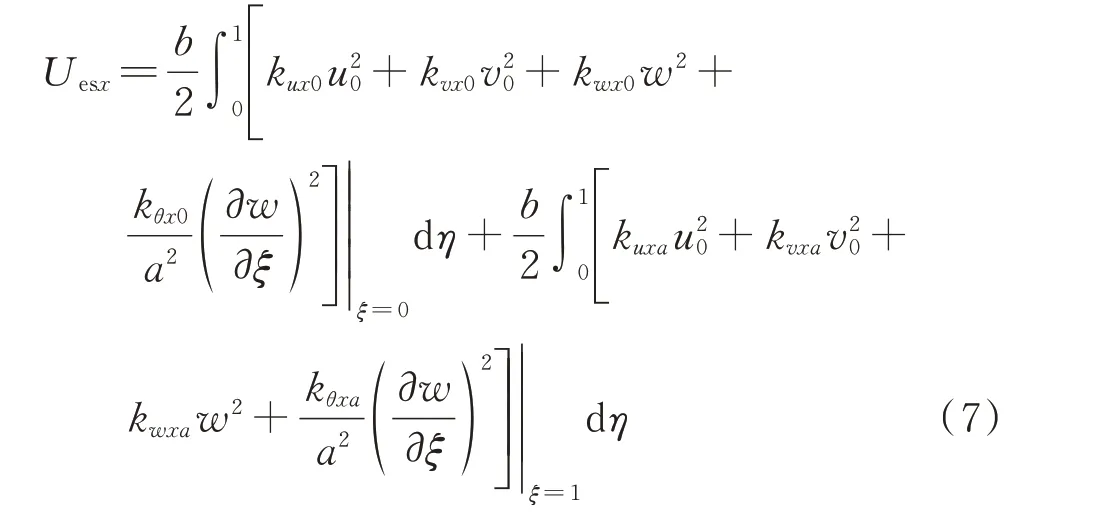
相似地，弹性边界η=0 和1 时的势能可表示为：

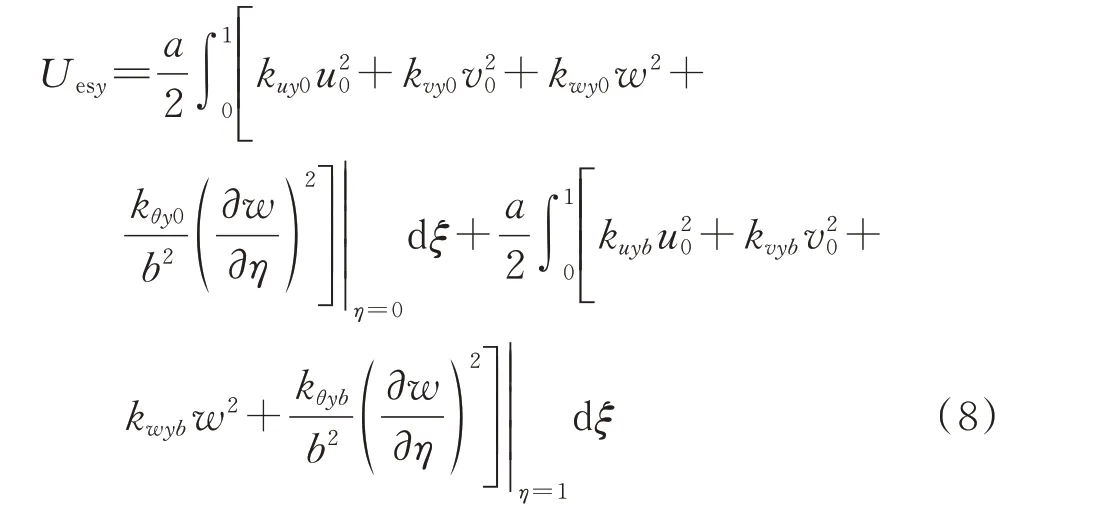
当平动弹簧及旋转弹簧的刚度增加到极大值（比如1010N/m2或1010N/rad），此时结构的边界条件为固支边界。相反，当平动弹簧和旋转弹簧的刚度为0 时，结构边界为完全放松的自由边界。以边界x=0 为例，固支（C）、简支（S）和自由边界（F）条件所对应的弹簧刚度可分别表示为：

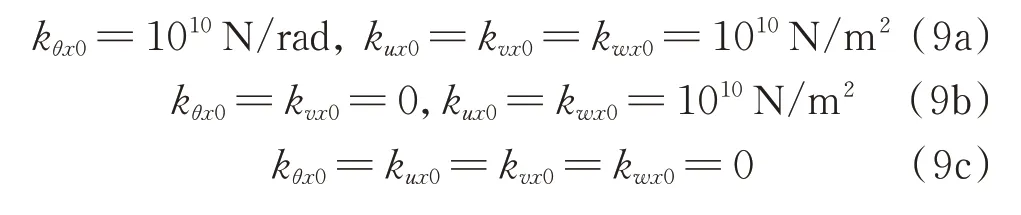
1.3 瑞利-里茨法

矩形板结构的未知位移函数可以写为：

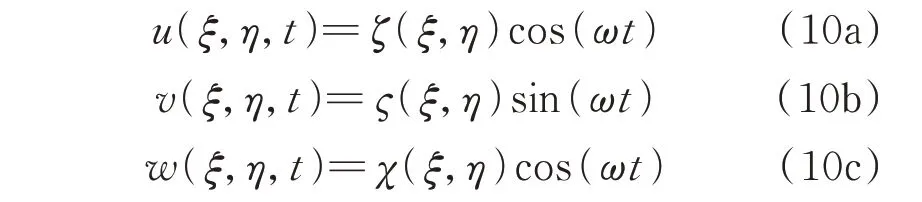
式中ω为结构固有圆频率；ζ（ξ，η），ς（ξ，η）和χ（ξ，η）为模态形函数，可以写成如下多项式形式：

式中Mc和Nc表示截断特征多项式项数；amn，bmn和cmn代表未知的多项式系数；和为特征多项式。

利用Gram-Schmidt 方法构造的多项式满足正交性，计算收敛性好。此外，只要特征正交多项式的首项满足矩形板的几何边界条件，正交多项式的其他项也就能满足结构的几何边界条件。因此，只要给出特征多项式的首项，就可以基于Gram-Schmidt 方法构造在积分域0 ≤ϖ≤1 内的一系列多项式如下［15-17］：

其中

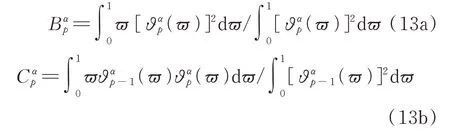
由式（12）计算得出的多项式ϑαp(ϖ)满足以下正交条件：

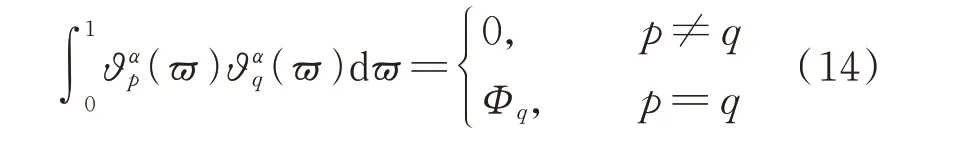
对特征正交多项式做如下的标准化处理：

表1 给出了5 种不同经典边界条件的多项式首项来构造相应的特征正交多项式。对于经典边界约束，例如S-S，C-C，C-F 及C-S 等，用表1 给出的多项式首项来构造特征多项式［16］。选择ϑα1（ϖ）=1 作为特征正交多项式的首项来计算弹性约束矩形板的模态形函数。

表1 5 种不同经典边界条件的特征多项式首项Tab.1 The first term of characteristic polynomial terms of five different classical boundary conditions

弹性边界约束矩形板的能量函数可表示为：

式中Ues=Uesx表示弹性边界ξ=0 或1 的势能。如果弹性边界沿η=0 或1，此时弹性边界的势能函数Ues=Uesy。

基于瑞利-里茨法，多项式系数amn，bmn和cmn需要使能量函数Ene达到最小值：

式中m=1，2，···，Mc；n=1，2，···，Nc。

把式（10）和（11）代入式（7）和（8）可以获得弹性边界势能的表达式Ues，之后把动能T、势能U及弹性边界势能Ues通过式（16）代入方程（17），可以得到关于弹性边界约束矩形板的特征方程：

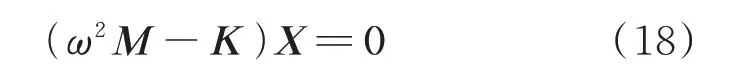
式中M和K为系数矩阵，X=[aT，bT，cT]T，其中a，b和c可以表示为：

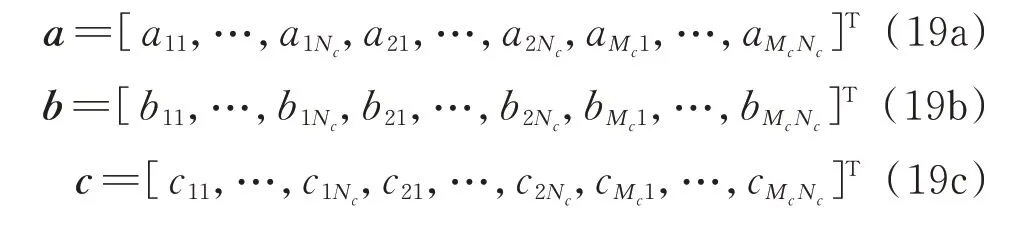
通过求解特征方程（18），可以获得弹性边界约束矩形板结构的固有频率及模态振型函数。

2 计算结果与实验验证

本节基于实验方法测试了不同弹性边界矩形板结构的固有频率，并与理论计算结果进行对比。矩形板结构的几何尺寸和材料参数为：a=b=0.5 m，h=0.005 m，ρ=1190 kg/m3，E=3×109N/m2，υ=0.4。用来模拟弹性边界的平动弹簧刚度为ke=530 N/m。在实验测试中，冲击锤用来激励矩形板结构，加速度传感器粘贴在矩形板结构表面。数据采集和处理系统用来接收传感器传输的信号。

图2（a）～（c）分别为一边固支、三种不同弹性边界条件下矩形板的振动测试图。结构的固定约束端用夹子固定在两块钢板上。为防止弹簧扭动，边界弹簧安装在3D 打印的弹簧支座上，并把弹簧支座粘贴在可近似看成刚体的实验台上。矩形板结构边界弹簧个数为11，因此弹性边界线弹簧的刚度Kew可以表示为：

图2 不同边界条件下矩形板结构振动测试图Fig.2 Vibration test diagrams of the rectangular plate under different boundary conditions

利用实验测试装置，测得不同边界下矩形板结构的幅频响应曲线如图3所示，其中纵坐标中的幅值g=9.8 m/s2表示重力加速度。基于结构实测频响曲线可求出结构的固有频率，其具体数值如表2所示。此外，表2 还给出了本文方法计算所得理论解、有限元仿真结果以及理论计算所得固有频率ft和实验测试固有频率fe之间的误差e，其计算公式为：

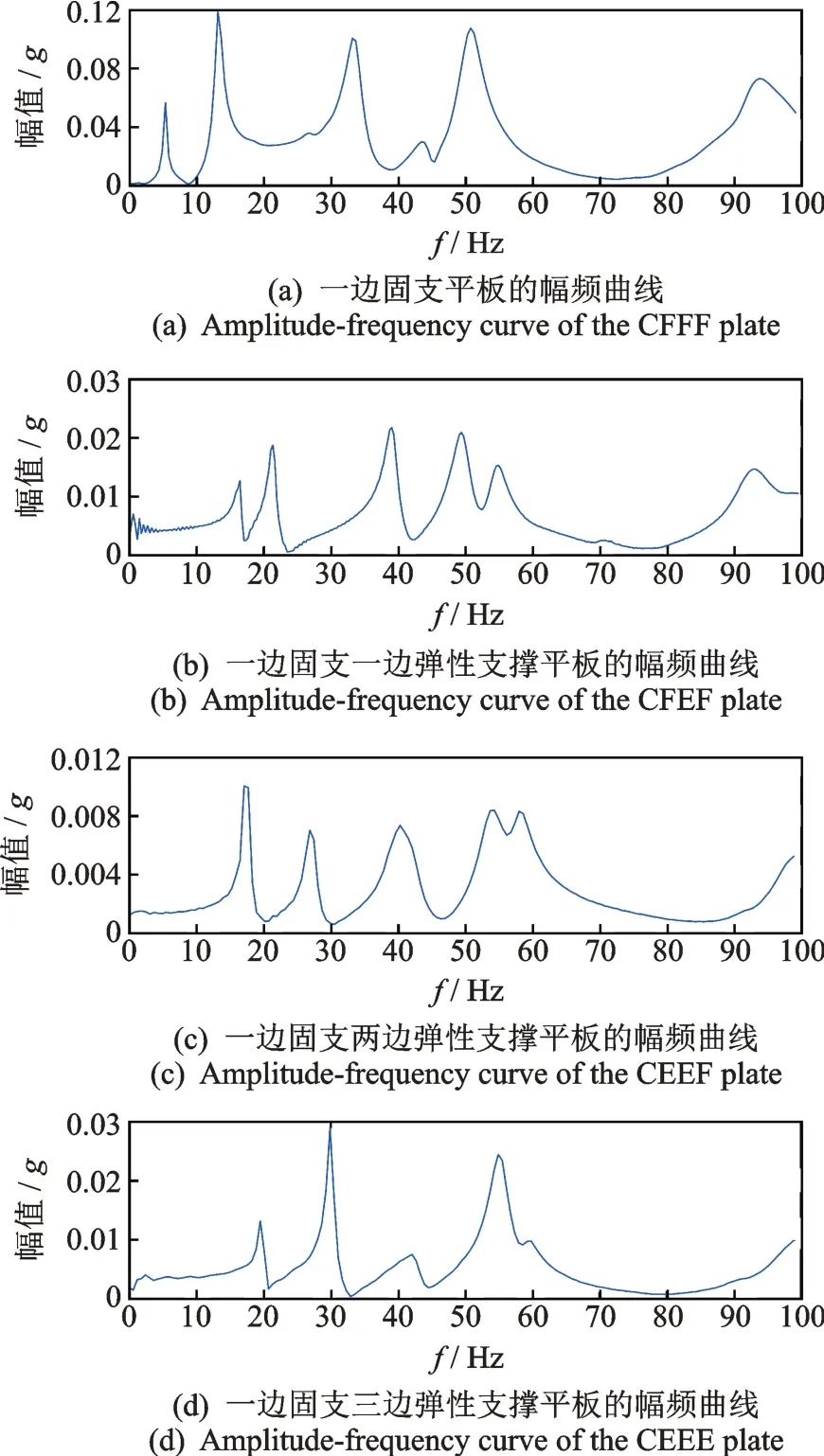
图3 不同边界条件下实测平板结构幅频曲线Fig.3 Amplitude-frequency curves of the measured plate with different boundary conditions

使用有限元软件COMSOL 中，采用的单元类型为四面体网格，单元个数为19072。软件中矩形板固支端设置为固定约束，弹性边界设置为弹性约束。由表2 可知，理论、有限元仿真及实验求得的一端固支弹性边界矩形板的固有频率吻合良好，这就证明了本文理论模型的正确性。

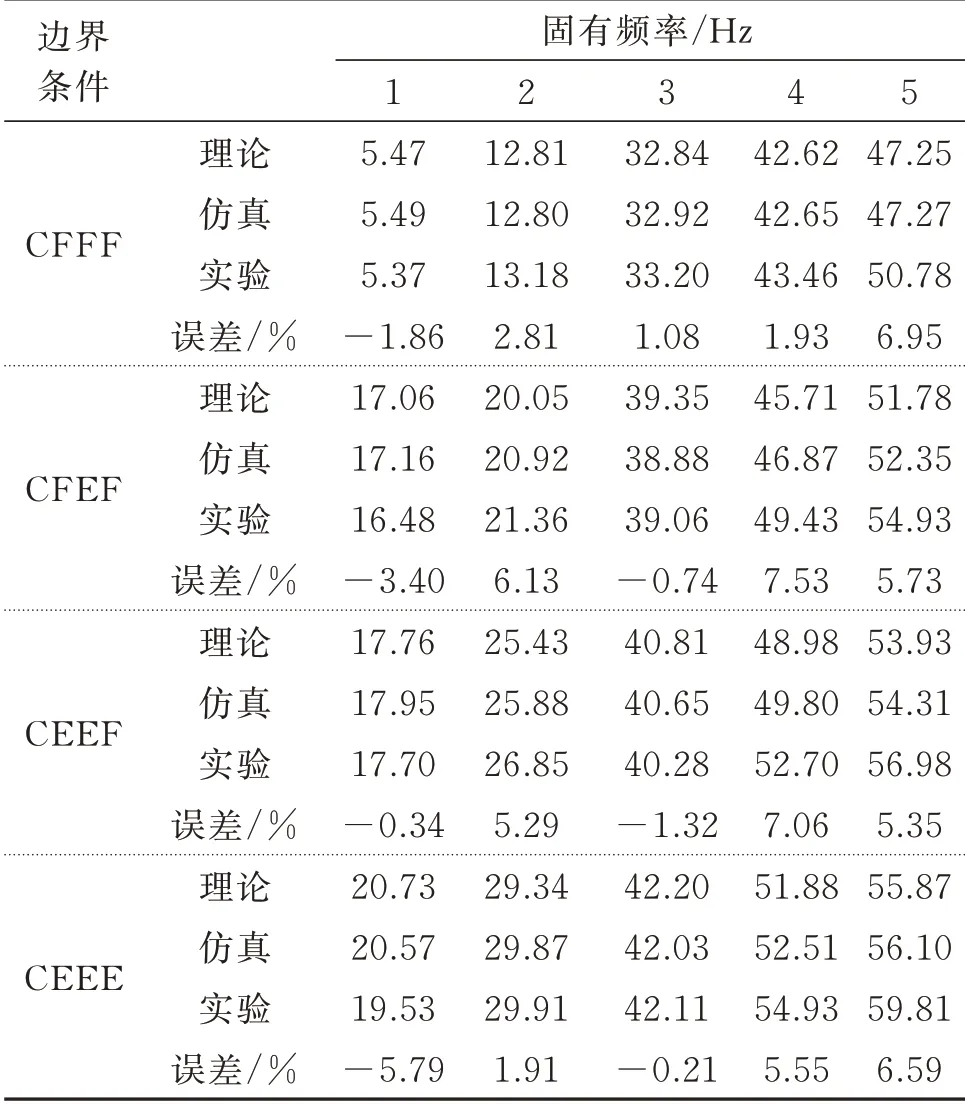
表2 不同弹性边界条件下平板的固有频率Tab.2 Natural frequencies of the plates under different elastic boundary conditions

为了验证平动弹簧以及旋转弹簧的刚度取值为1010N/m2和1010N/rad时模拟矩形板固支边界的合理性及计算结果的精确性，计算了不同边界弹簧刚度下矩形板的固有频率，并与一端固支矩形板有限元仿真结果进行对比，如表3所示。从表3 中可以看出，当平动弹簧以及旋转弹簧刚度取1010N/m2和1010N/rad时，计算结果已经收敛，且和仿真结果吻合良好。因此在计算中平动弹簧及旋转弹簧刚度取1010N/m2和1010N/rad来模拟固支边界是完全满足计算精度要求的。

表3 不同弹簧刚度下矩形板的固有频率/HzTab.3 Natural frequencies of the rectangular plates under different spring stiffness/Hz

此外，基于实验方法研究了四边简支、一边简支一边弹性支撑及对边简支对边弹性支撑矩形板的固有特性。图4 为实验测试中矩形板简支边界原理示意图。其中设计加工了上、下两根刚性圆柱杆固定矩形板的边界，上、下圆柱杆通过预紧的螺栓固定，这样既能够限制矩形板边界的横向位移，又能够保证矩形板边界自由地转动，从而准确有效地模拟矩形板结构的简支边界条件。

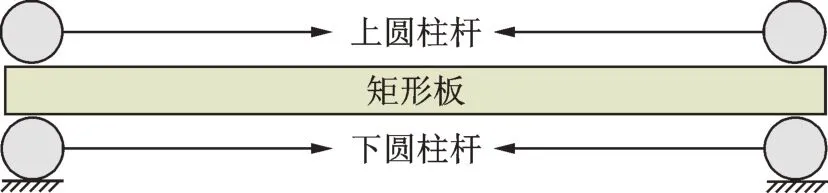
图4 矩形板简支边界原理示意图Fig.4 Schematic diagram of simply supported boundary principle of the rectangular plate

图5 为简支弹性支撑矩形板实验测试装置。由于支座安装的原因，此实验下矩形板的长度和宽度分别为a=0.526 m 和b=0.529 m。矩形板弹性边界上安装的弹簧为11 个，结构其他参数和固支弹性支撑时一致。图6所示为基于实验装置测得的四边简支、一边简支一边弹性支撑及对边简支对边弹性支撑矩形板的幅频响应曲线。实测结构的前5 阶固有频率如表4所示。基于本文理论计算以及有限元数值仿真的结果也在表4 给出，同时给出了理论计算结构固有频率和实测结构固有频率的误差。有限元数值仿真中，采用的单元类型为四面体网格，单元个数为19166。从表4 中可以看出，三者计算结果有很好的一致性，误差不超过7.8%。通过两根圆柱杆夹紧固定矩形板边界可能产生小的横向位移，弹性边界弹簧刚度测量的准确性以及矩形板结构材料属性和理论的差异是引起误差的可能原因。尽管如此，理论、仿真以及实验之间的结果吻合良好，证实了本文平板结构简支边界及弹性边界设计的合理性及理论计算的正确性。

图5 不同边界条件下平板结构振动测试图Fig.5 Vibration test diagrams of the plate under different boundary conditions

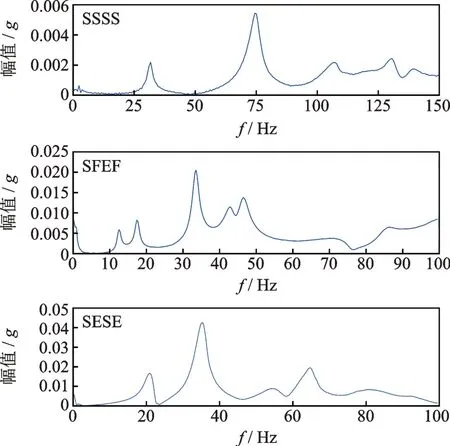
图6 不同边界条件下实测平板结构幅频曲线Fig.6 Amplitude-frequency curves of the measured plate structure with different boundary conditions

表4 不同弹性边界条件下平板的固有频率Tab.4 Natural frequencies of the plates under different elastic boundary conditions

3 弹性边界矩形板振动特性分析

对于给定阶次的频率，其对应的特征向量可以由式（18）求出。特征向量对应该矩形板在给定阶次模态频率所对应振型的多项式展开系数，将系数代入式（11）表征的容许函数中，即可获得矩形板结构的模态振型。图7～10 分别给出基于理论方法和有限元软件COMSOL 计算所得三边简支一边弹性支撑（SSSE）和两边固支两边弹性支撑（CCEE）矩形板的第一阶和第二阶模态振型图。对于SSSE 矩形板，弹性边为右边界；而对于CCEE 矩形板，弹性边为右边界和下边界。弹性边只含有平动弹簧，其刚度为105N/m2。使用有限元软件COMSOL 计算时，采用的单元类型为四面体网格，单元个数为25907。从图7～10 中可以看出，本文理论计算结构振型和有限元结果一致，进一步说明了本文理论计算的有效性。

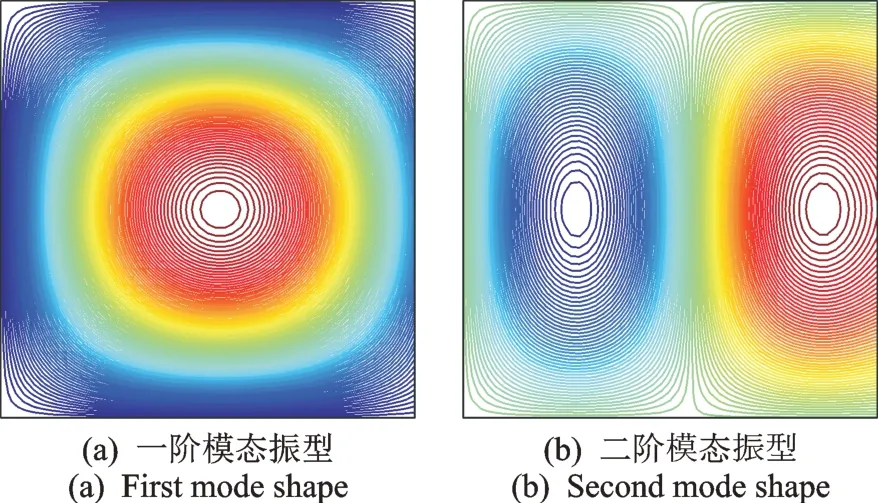
图7 理论计算SSSE 矩形板的振型Fig.7 Vibration mode of the SSSE rectangular plate using theoretical calculation

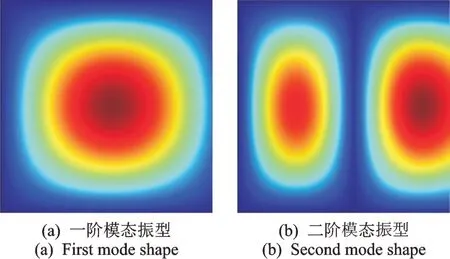
图8 有限元软件COMSOL 计算SSSE 矩形板的振型Fig.8 Vibration mode of the SSSE rectangular plate using finite element software calculation

图10 有限元软件COMSOL 计算CCEE 矩形板的振型Fig.10 Vibration mode of the CCEE rectangular plate using finite element software calculation

为研究矩形板从一边固支三边自由（CFFF）状态到对边固支对边自由（CFCF）时的振动特性，通过改变边界弹簧刚度模拟结构不同的边界。控制边界x=0 弹簧刚度kwx0=1010N/m2和kθx0=1010N/rad，将沿边界x=a的弹簧刚度kwxa和kθxa从0 增加到1010N/m2和1010N/rad。图11所示为矩形板一阶固有频率随kwxa和kθxa的变化关系。从图11 中可知，矩形板的固有频率随边界x=a弹簧刚度kwxa和kθxa的增大而增大。当旋转弹簧刚度kθxa在10～1000 N/rad 范围内变化时，结构的一阶频率有较大的变化；而当平动约束弹簧刚度kwxa在100～106N/m2范围内变化时，结构的第一阶固有频率变化明显。此外，相对于旋转弹簧，平动弹簧刚度的增加能更加有效地提高结构的固有频率。

通过改变弹簧刚度kwxa及kwy0，可使矩形板从CFFF 变为CSSF 边界。矩形板的一阶固有频率随弹簧刚度kwxa及kwy0的变化如图12所示。由图12 可知，结构一阶固有频率随平动弹簧刚度kwxa及kwy0的增大而增大。但是，平动弹簧刚度kwy0的增加对结构固有频率的提升作用非常有限，而增加平动弹簧刚度kwxa能够有效地提高结构的固有频率。

图12 一阶固有频率随kwxa及kwy0的变化关系Fig.12 Variation relationship of the first order natural frequency with kwxa and kwy0

通过改变矩形板旋转弹簧刚度kθy0及kθyb，能够使CSSS 矩形板变为CCSC 矩形板，结构一阶固有频率的变化如图13所示。从图13 中可以看出，当旋转弹簧刚度在0～104N/rad 范围时，随着旋转弹簧刚度的增加，结构的一阶固有频率明显增加。当旋转弹簧刚度大于104N/rad 时，结构的固有频率基本不变。由此可以得出矩形板的固有频率随旋转弹簧刚度变化的敏感区间为0～104N/rad。

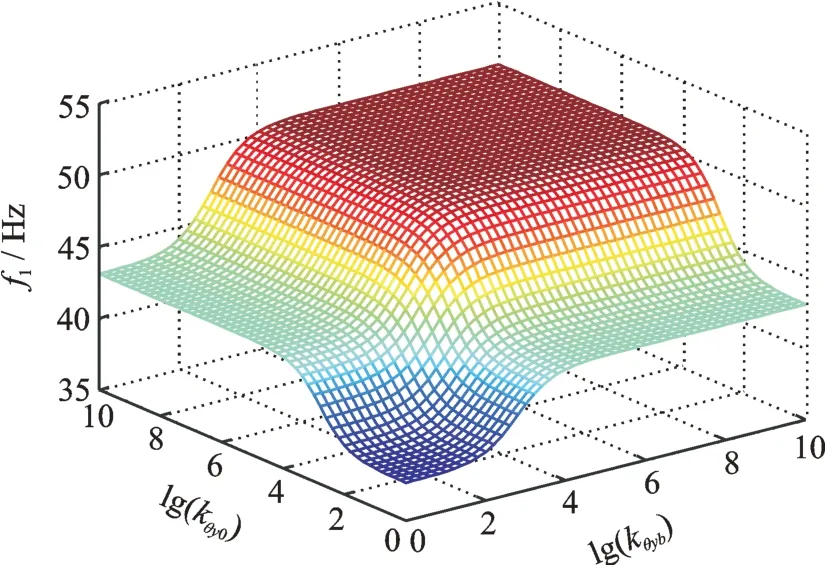
图13 一阶固有频率随kθy0及kθyb的变化关系Fig.13 Variation relationship of the first order natural frequency with kθy0 and kθyb

4 结论

本文采用特征正交多项式表示位移容许函数，建立了弹性约束矩形板结构振动特性分析模型。利用瑞利-里茨法获得弹性边界约束矩形板的固有频率和振型，并与有限元及实验结果进行对比，验证了本文所提理论方法的正确性和可靠性。详细分析了调整不同边界弹簧刚度对矩形板振动特性的影响，得到的主要结论如下：

（1）采用特征正交多项式描述结构横向位移，结合瑞利-里茨法获得弹性边界约束矩形板的固有频率和振型。对不同结构参数、边界条件的矩形板求解，仅需修改结构参数，无需重新建模。

（2）设计实验测试了弹性-简支、弹性-固支等不同边界组合矩形板的固有频率，并与本文理论方法和有限元结果进行了对比，验证了矩形板弹性边界设计的合理性及理论计算的正确性。

（3）矩形板的固有频率随着边界弹簧刚度的增大而增大。相对于旋转弹簧，平动弹簧刚度的增加能更加有效地提高结构的固有频率。

（4）当旋转弹簧刚度在0～104N/rad 内变化时，本文所研究矩形板结构的一阶固有频率变化明显；其固有频率随旋转弹簧刚度变化的敏感区间为0～104N/rad。