确定性周期与随机激励联合作用下非线性系统非平稳响应的统计线性化方法

孔 凡，韩仁杰，张远进

（1.武汉理工大学土木工程与建筑学院，湖北武汉 430070；2.合肥工业大学土木与水利工程学院，安徽合肥 230009；3.武汉理工大学安全科学与应急管理学院，湖北武汉 430070）

引言

工程动力作用具有强烈的随机性，通常利用非平稳随机过程描述［1］。以完全非平稳地震动为例：它不仅在强度上具有明显的上升和衰减过程，而且在不同时间段上能量的频率分布也不同［2］。因此，地震动非平稳性体现为幅值非平稳和频率非平稳。学者们提出了各种模型以全面反映地震动的非平稳特性［3-6］。近年来，小波变换以其时-频联合分辨特性在地震动建模方面得到了广泛发展，详见文献［7-10］。

复杂非线性系统在随机激励下的随机动力响应是随机振动研究的重要课题。具体而言，利用Fokker-Planck-Kolmogorov（FPK）方程［11］、随机平均法［12］、统计线性化（或非线性化）［13］、矩截断［14］、信息理论（熵）方法［15］以及最近发展的概率密度演化方法［16］等，人们已解析或数值地得到了很多非线性随机动力系统的精确解或近似解。然而，高效地计算非平稳激励下复杂非线性系统的非平稳响应仍然是工程随机振动理论发展面临的巨大挑战［17］，具有重要的实际意义。统计线性化方法是随机振动理论中具有广泛适用性的非线性方法之一。它可以用于不同的无记忆非线性［18］，甚至滞回非线性系统［19］、平稳或非平稳随机激励［17］、多自由度［20］或连续系统［21］，最近的文献综述详见文献［22］。

上述研究仅考虑激励为随机过程的情况。然而，工程实际中，结构往往会同时受到确定性周期和随机激励的联合作用。例如，旋转式飞机［23］经常受到色噪声和谐波激励联合作用；俘能系统的非线性响应［24］；近断层脉冲地震作用下的结构等。为此，人们发展了联合激励下非线性系统随机动力响应的系列方法：Chang［25］使用高斯与非高斯线性化求得了Duffing 系统在谐波与高斯白噪声激励联合作用下的平稳响应；Chen 等［26］给出了分数阶Duffing 系统在确定性激励与平稳白噪声联合作用下平稳响应的随机平均法；Zhu 等［27］利用谐波平衡和矩截断方法研究了Duffing 系统在谐波与随机激励联合作用下的平稳响应；Zhang 等［28］给出了周期与随机激励联合作用下多自由度齿轮结构平稳响应的统计线性化方法。然而，考察联合激励下非平稳随机作用带来的响应非平稳性，尚未引起人们足够的重视。这种随机响应的非平稳性主要来自于三个方面：突加激励非平稳、与谐波响应耦合的非平稳、随机激励自身的变慢非平稳。

注意到统计线性化方法的广泛适用性，本文提出了一种用于求解确定性周期与非平稳随机激励联合作用下、单自由度非线性系统非平稳响应的统计线性化方法，可视为作者发展的平稳方法的非平稳推广［29-30］。该方法将系统响应分解为确定性谐波和零均值随机分量之和，将原非线性运动方程等效地化为一组耦合的、分别以确定性和随机动力响应为未知量的非线性微分方程。然后，利用统计线性化方法将非平稳随机激励作用下的非线性随机动力方程化为等效线性方程，得到关于线性随机响应二阶矩的李雅普诺夫微分方程。最后，联立李雅普诺夫微分方程与谐波激励作用下的确定性微分方程，通过数值算法（如龙格-库塔法）对这组耦合非线性常微分方程进行求解。数值算例中，利用蒙特卡洛模拟验证此方法的适用性和精度。

1 动力学方程

单自由度非线性系统在确定性周期和非平稳随机激励联合作用下的运动方程为：

式中m，c和k分别为质量、阻尼和刚度系数；和分别为响应的位移、速度和加速度；为和的非线性函数；Q(t)为零均值均匀调制非平稳随机激励，可写为：

式中a(t)为调制函数；Qs(t)为零均值平稳随机过程；F(t)为确定性周期激励，写为Fourier 展开形式为：

式中Fl为第l次谐波幅值。

激励的非平稳性导致响应的非平稳性。这里，响应的非平稳性主要来自于：突加激励、谐波激励谐和变化以及随机激励幅值慢变非平稳。假设响应x(t)可分解为均值μx(t)和方差为的零均值非平稳随机过程之和，即：

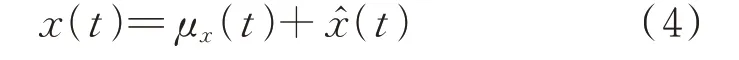
同时，

式中 D[·]表示方差。将式（4）代入式（1）中得：

为方便计，省略了响应量的时间参数。对式（6）两边求数学期望得：

式中 E[·]表示数学期望，用式（6）减式（7）得：

式中

2 统计线性化方法

利用统计线性化方法将式（8）化为线性方程：

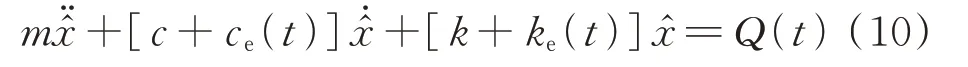
式中ce(t)，ke(t)为等效线性参数。当随机激励Q(t)为高斯过程时，响应x^ (t)也为高斯过程；即使Q(t)为非高斯过程，当系统阻尼较小时，响应也可近似为高斯过程。因此，ce(t)，ke(t)均为时间t的函数，且有：

以下考虑Qs(t)为白噪声和色噪声两种情况。

2.1 Qs(t)为白噪声

此时，Q(t)为均匀调制白噪声，即：

式中w(t)为零均值高斯白噪声，功率谱密度为S0。将式（10）化为状态方程的形式：

与式（13）对应的李雅普诺夫方程为：

式中v为响应的协方差矩阵，即：

vij(t)为响应(qi，qj)，i，j=1，2 的方差/协方差，且vij(t)=vji(t)；Θ(t)为激励Q(t)的协方差矩阵，即：

结合响应的高斯性可知，期望：

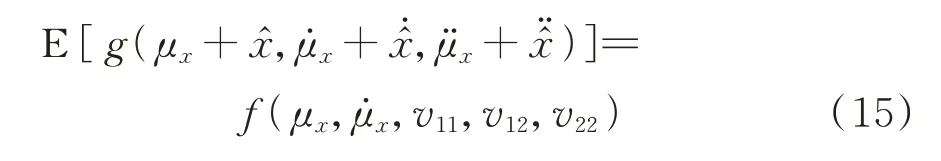
可得

所有未知量的初始值均为零，可利用龙格-库塔法求解式（16）～（20），得响应的确定性分量时程与随机分量协方差矩阵。

2.2 Qs(t)为色噪声

此时，Q(t)为均匀调制色噪声，平稳随机过程Qs(t)的功率谱密度为S(ω)。将式（2）中的Qs(t)表示为白噪声经过成型滤波器的形式，即：

式中Φ为滤波器的前置输出，n为成型滤波器维度；Φ(i)表示Φ的第i阶导数；λ0，λ1，…，λn-1和ν0，ν1，…，νn-1为滤波器参数；w(t)为零均值高斯白噪声，功率谱密度为S0。令：

则式（22）可以写为：

式中

令：

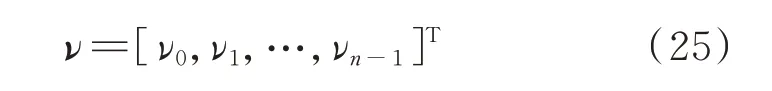
则式（21）可写为：

联立式（8）、式（24）和式（26），得：

与式（27）对应的李雅普诺夫方程为：

式中

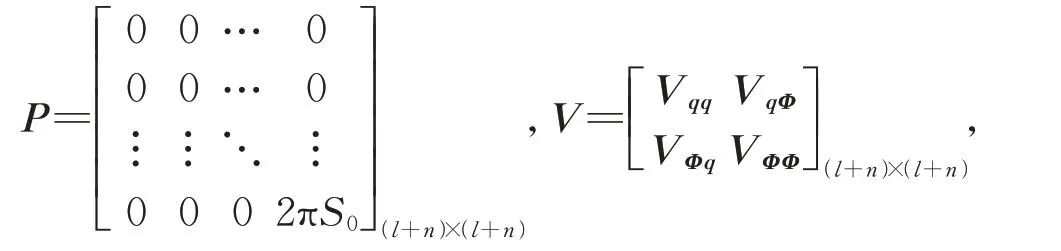
且Vqq=E{qqT}，VqΦ=VΦq=E{qΦT}VΦΦ=E{ΦΦT}。

同样地，将式（28）与式（7）联立，可利用数值方法求解得到所有未知量需要注意的是，VΦΦ的值仅与色噪声本身有关，可直接确定。具体的计算步骤将在算例中进一步说明。

3 数值算例

作为算例，不失一般性地考虑具有立方非线性刚度的Duffing 振子，即：

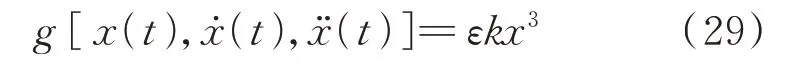
式中ε为表示非线性强度的小量。式（7）中非线性项的数学期望为：

从而，式（7）可写为：

同样地，式（8）可化为：

依据式（11），等效线性参数为：

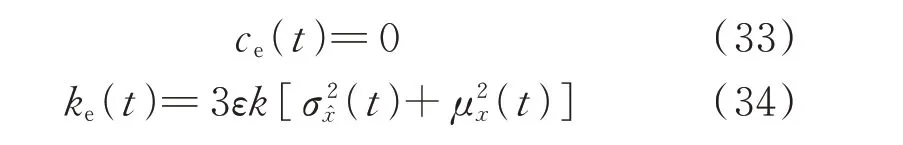
式（13）中，系数矩阵：

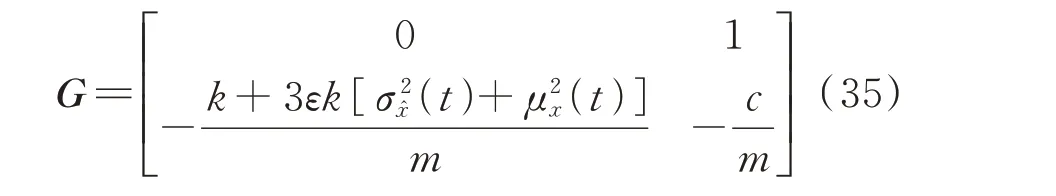
如果确定性激励为单谐波的形式，即：

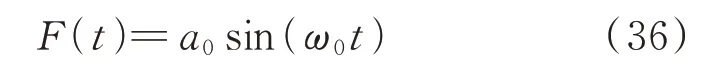
式中a0为确定性激励幅值，ω0为确定性激励频率。

假定调制函数：

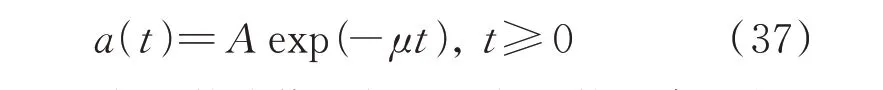
式中A为调制函数峰值，μ标识调制函数下降速度。

3.1 Qs(t)为白噪声

此时，Q(t)为均匀调制白噪声，即：

将式（33）～（37）代入式（16）～（20）中，利用数值方法求得y，即所有确定性与随机响应分量。

3.1.1 典型参数设置的情况

选取系统参数m=1，c=0.4，k=1，ε=0.5；确定性激励参数a0=1，ω0=1 rad/s；随机激励参数本文利用蒙特卡洛模拟（Monte Carlo simulation，MCS）验证所建议方法的适用性。其中，利用谱表现方法生成白噪声样本10000 条，乘以调制函数得均匀调制白噪声。利用本文所建议方法与MCS 得到了位移均值及其标准差，其对比如图1（a），（b）所示。

图1 Duffing 系统在谐波与调制白噪声联合作用下的位移Fig.1 Displacement of the considered Duffing system subjected to combined harmonic and modulated white noise

从图1（a），（b）可以看出，在考虑的参数设置情况下，本文建议方法（Proposed Method，PM）与蒙特卡洛模拟的均值几乎完全吻合。在随机响应分量标准差方面，所建议方法能很好地捕捉由于突加激励（由0 上升的过程）、确定性谐和激励分量（下降过程中呈谐和变化）和随机激励分量调制函数带来的非平稳性（慢变的上升-下降过程）。

3.1.2 非线性强度的影响

下面分析此方法在不同非线性强度下的适用性。其他参数与3.1.1 节选取相同，非线性强度系数ε取0～1。定义确定性谐和分量平均功率为：

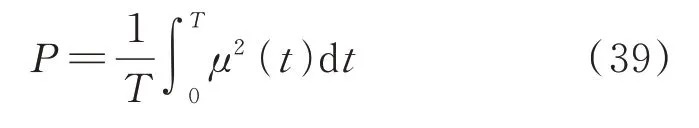
式中T为响应持时。定义随机响应分量标准差的时间平均为：采用所建议方法与蒙特卡洛模拟计算得到的确定性响应分量平均功率对比如图2所示，标准差时间平均对比如图3所示。

图2 非线性强度对Duffing 系统确定性响应平均功率的影响Fig.2 Averaged power of the deterministic response component of the Duffing system with different degrees of nonlinearity

图3 非线性强度对Duffing 系统随机响应标准差时间平均的影响Fig.3 Time-averaged standard deviation of the stochastic response component of the Duffing system with different degrees of nonlinearity

从图2，3 可见，在其他参数不变的情况下，确定性响应平均功率随着非线性强度增加而降低；位移标准差的时间平均随非线性强度增加而降低，速度响应标准差的时间平均随非线性强度增加而略有减小。所有非线性强度情况下，两种方法所得结果均吻合较好。

3.1.3 激励幅值的影响

为研究确定性激励幅值对此方法适用性的影响，保持其他参数不变，确定性激励幅值a0取0～2 rad/s。利用本文所建议方法与蒙特卡洛模拟计算得到的确定性响应分量平均功率对比如图4所示；时变标准差的时间平均对比如图5所示。

图4 谐波激励幅值对Duffing 系统确定性响应平均功率的影响Fig.4 Averaged power of the deterministic response component versus the harmonic excitation amplitude

图5 谐波激励幅值对Duffing 系统随机响应标准差时间平均的影响Fig.5 Influence of the harmonic excitation amplitude on the time-averaged standard deviation of the response

由图4，5 可见，在其他参数不变的情况下，确定性响应平均功率随谐波激励幅值增大而增大；位移标准差的时间平均随谐波激励幅值增大而减小，速度标准差的时间平均随谐波激励幅值增大而增大。不同激励幅值下，两种方法所得的结果均吻合较好。

3.1.4 确定性谐和激励频率的影响

为研究确定性激励频率对此方法适用性的影响，保持其他参数不变，确定性激励频率ω0取0.1～2 rad/s。采用本文所建议方法与蒙特卡洛模拟得到的确定性响应分量的平均功率对比如图6所示；随机响应非平稳标准差的时间平均如图7所示。

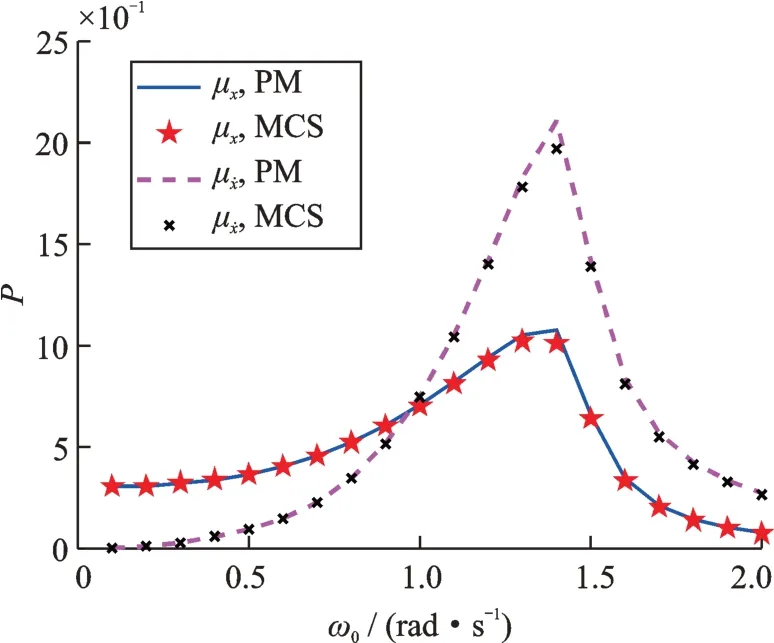
图6 谐波激励频率对Duffing 系统确定性响应平均功率的影响Fig.6 Influence of the harmonic excitation frequency on the averaged power of the deterministic response component

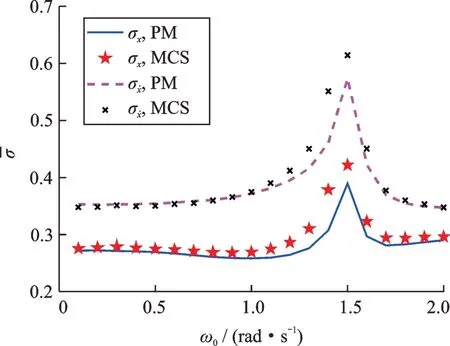
图7 谐波激励频率对Duffing 系统随机响应标准差时间平均的影响Fig.7 Influence of the harmonic excitation frequency on the time-averaged standard deviation of the response

可见，谐波激励频率对确定性响应平均功率和随机响应标准差平均有较大影响，存在使他们达到极值的谐波激励频率。其中，使确定性响应平均功率达到最大的谐波激励频率约为1.4 rad/s，而使随机响应标准差时间平均值达到最大的谐波激励频率约为1.5 rad/s。此外，不同激励频率下本文所建议的方法与蒙特卡洛模拟所得结果均吻合较好。

3.1.5 随机激励强度的影响

为研究随机激励强度对此方法适用性的影响，保持其他参数不变，功率谱强度S0取0～1。采用本文所建议方法与蒙特卡洛模拟得到的确定性响应分量平均功率对比如图8所示；随机响应时变标准差的时间平均对比如图9所示。

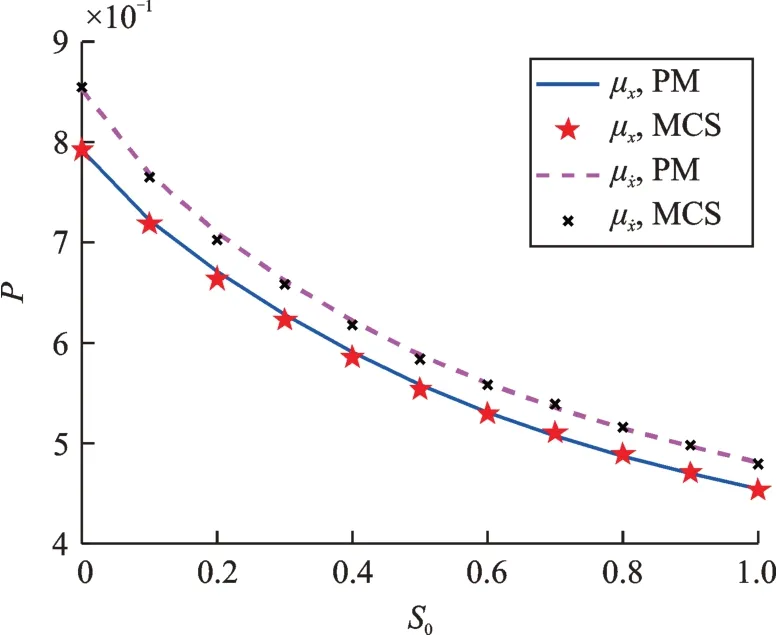
图8 随机激励功率谱强度对Duffing 系统确定性响应功率的影响Fig.8 Influence of the stochastic excitation power spectral density on the averaged power of the deterministic response component

图9 随机激励功率谱强度对Duffing 系统随机响应标准差时间平均的影响Fig.9 Influence of the stochastic excitation power spectral density on the time-averaged standard deviation of the response

可见，随机激励功率谱强度对确定性响应平均功率和随机响应标准差平均有较大影响。由图8，9 可知随着随机激励功率谱强度的增大，确定性响应平均功率逐渐减小，随机响应标准差的时间平均逐渐增大。所有随机激励强度下两种方法所得结果均吻合较好。

综上，对于Duffing 系统在确定性谐波与调制白噪声联合作用下的响应，本文所建议的方法在不同参数设置情况下均有良好的适用性。

3.2 Qs(t)为色噪声

令Q(t)为均匀调制色噪声，即：

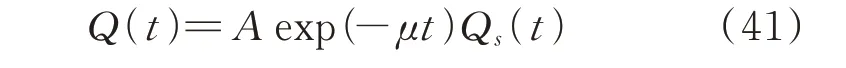
式中Qs(t)为平稳色噪声。设功率谱密度为金井清谱［31］的形式：

式中ζg为场地阻尼比，ωg为特征周期。则成型滤波器的维度n=2，式（21）和（22）退化为：

式中

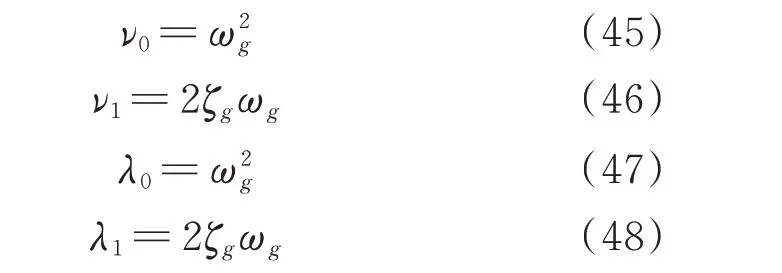
则式（24）中

式（26）中

且式（28）中

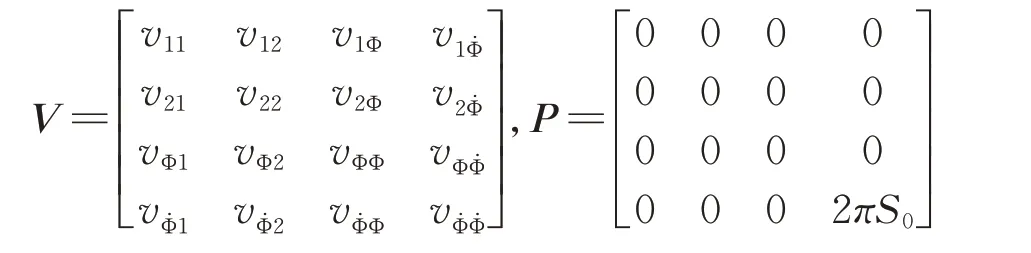
将式（35），（49）和式（50）代入式（28）中，并与式（31）联立，可得一组微分方程，具体步骤可见文献［18］。

用龙格-库塔法解此非线性常微分方程组可得响应确定性与随机分量。

3.2.1 典型参数设置的情况

选取系统参数m=1，c=0.4，k=1，ε=0.5；确定性激励参数a0=0.5，ω0=1.2 rad/s；随机激励参数利用谱表现方法生成色噪声样本10000条。

利用本文所建议方法与蒙特卡洛模拟得到了位移的非平稳均值及标准差，其对比如图10（a），（b）所示。

从图10（a），（b）可以看出，在考虑的参数设置情况下，本文建议方法与蒙特卡洛模拟的均值较吻合。在随机响应分量标准差方面，所建议方法能很好地捕捉突加激励、确定性激励分量和随机激励分量调制函数带来的非平稳性。

图10 Duffing系统在谐波与调制色噪声激励联合作用下的位移Fig.10 Displacement of the considered Duffing system subjected to combined harmonic and modulated colored noise

3.2.2 非线性强度的影响

同样地，保持其他参数不变，非线性强度系数ε取0～1。采用所建议方法与蒙特卡洛模拟计算得到的确定性响应分量的平均功率对比如图11所示；标准差时间平均对比如图12所示。

图12 非线性强度对Duffing 系统随机响应标准差时间平均的影响Fig.12 Time-averaged standard deviation of the stochastic response component of the Duffing system with different degrees of nonlinearity

从图11，12可以看出，在其他参数不变的情况下，确定性响应平均功率随着非线性强度增加先增大后降低；位移标准差的时间平均随非线性强度增加而降低；速度标准差的时间平均在非线性程度较小时略有升高，之后随非线性程度增加而减小。在所有非线性强度情况下，两种方法所得结果均吻合较好。

图11 非线性强度对Duffing 系统确定性响应平均功率的影响Fig.11 Averaged power of the deterministic response component of the Duffing system with different degrees of nonlinearity

3.2.3 激励幅值的影响

为研究确定性激励幅值对此方法适用性的影响，保持其他参数不变，确定性激励幅值a0取0～2。本文所建议方法与蒙特卡洛模拟计算得到的确定性响应分量的平均功率对比如图13所示，时变标准差的时间平均值对比如图14所示。

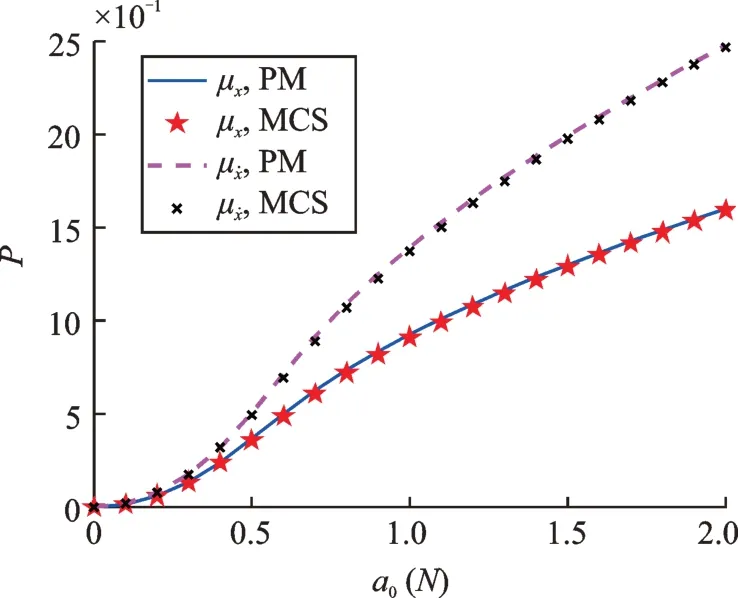
图13 谐波激励幅值对Duffing 系统确定性响应平均功率的影响Fig.13 Averaged power of the deterministic response component versus the harmonic excitation amplitude of the Duffing system

图14 谐波激励幅值对Duffing 系统随机响应标准差时间平均的影响Fig.14 Influence of the harmonic excitation amplitude on the time-averaged standard deviation of the Duffing system

由图13，14 可见，在其他参数不变的情况下，确定性响应平均功率随谐波激励幅值增大而增大；位移标准差的时间平均随谐波激励幅值增大而减小，速度标准差的时间平均随谐波激励幅值增大先增大后减小，这一点与图5所示的随机激励为白噪声的情况有所不同。在所有确定性激励幅值的情况下，两种方法所得的结果均吻合较好。

3.2.4 确定性谐和激励频率的影响

为研究确定性激励频率对此方法适用性的影响，保持其他参数不变，确定性激励频率ω0取0.1～2 rad/s。本文所建议方法与蒙特卡洛模拟得到的确定性响应分量的平均功率对比如图15所示；随机响应非平稳标准差的时间平均如图16所示。

图15 谐波激励频率对Duffing 系统确定性响应平均功率的影响Fig.15 Influence of the harmonic excitation frequency on the averaged power of the deterministic response component

图16 谐波激励频率对Duffing 系统随机响应标准差时间平均的影响Fig.16 Influence of the harmonic excitation frequency on the time-averaged standard deviation of the response

可见，谐波激励频率对确定性响应平均功率和随机响应标准差的时间平均有较大影响，存在使它们达到极值的谐波激励频率。对于前者，达到极值的频率为1.2 rad/s；对于后者，达到极值的频率为1.3 rad/s。此外，不同激励频率下本文所建议方法与蒙特卡洛模拟所得结果均吻合较好。

综上所述，对于Duffing 系统在确定性谐波与随机激励联合作用下的响应，本文所建议方法在不同参数设置的情况下，均有良好的适用性。所建议方法的计算效率较蒙特卡洛模拟有显著优势。以调制白噪声与确定性激励联合作用下的响应计算为例，所建议方法仅需0.01 s，而10000 个样本的蒙特卡洛模拟需要1.62 s，效率提高162 倍。

4 结论与展望

提出了一种用于求解确定性谐波与非平稳随机激励联合作用下，单自由度非线性随机动力系统非平稳响应的统计线性化方法。首先，将系统响应分解为确定性周期和零均值随机分量之和，得到了与原非线性运动方程等效的、两个耦合的且分别以确定性和随机动力响应为未知量的非线性运动微分方程。随后，利用非平稳统计线性化方法，将得到的非线性随机运动方程化为了等效线性方程。最后，同时考虑与等效线性随机微分方程对应的李雅普诺夫方程和谐波激励下的确定性运动方程，利用数值方法联立求解了所有确定性未知量与随机未知量。蒙特卡洛模拟验证了此方法的适用性和精度。

数值算例表明，无论随机噪声为调制白噪声或调制色噪声，该方法均能准确地求解系统的确定性周期响应；求解的随机动力响应分量的非平稳二阶矩也具有较好的精度。此外，该方法适用于不同的参数设置情况。可进一步将该方法拓展应用于（多自由度）滞回非线性系统和分数阶非线性系统、（不可分）完全非平稳激励等情况。