含参Bézier曲线在特征空间下的形状分析
刘 植, 王翠翠
(合肥工业大学 数学学院,安徽 合肥 230601)
Bézier方法是计算机图形学与计算机辅助几何设计领域的一个重要方法。为使曲线形状的控制手段更加丰富,研究者通过引入形状参数对Bézier曲线进行推广,得到各种类型的含参曲线[1-3],其中关于含参三次Bézier曲线的研究较为广泛[4-6]。在传统几何造型设计中,良好的曲线形状通常应该消除不必要的奇点(包括尖点、重结点)和拐点,关于含参曲线形状分布条件的进一步研究对于控制曲线的形状具有重要作用。文献[7]在研究三次Bézier曲线的几何特征时,提出基于仿射不变量的方法,并讨论了Bézier曲线的奇拐点分布;文献[8]提出一种基于控制顶点轨迹的方法,进一步分析了含参曲线的几何形状;文献[9]在研究平面B样条曲线的几何形状时,提出一种基于包络理论与拓扑映射的新方法(称作叶方法)。关于上述方法的研究已有比较成熟的成果,但这些方法都要进行分类讨论,算法较复杂,不利于程序的交互设计。文献[10]提出一种基于特征空间的形状分析方法,并利用该方法讨论了一类三角Bézier曲线的几何形状特征[11]。
本文基于特征空间的形状分析方法,讨论一类三次含参Bézier曲线的形状分布。通过化简参数曲线形状特征表达式中边向量的系数,得到含有参数的各特征锥面;对特征锥面及其相应切平面构成的空间区域进行切割,得到该曲线的形状特征分布。该方法计算量小,且包含除全部控制点共线情况外的所有退化结果。锥面方程中的形状参数λ具有优化曲线的调节能力,对调节控制曲线的形状特征具有重要的应用价值。
1 三次λ-Bézier曲线
任意给定平面上4个控制点Pi(i=0,1,2,3)及参数λ(其中λ∈(0,3],称为形状因子),三次λ-Bézier曲线[5]定义如下:
(1)
其中,bi,3(t)(i=0,1,2,3)是三次λ-Bernstein多项式,表达式为:
(2)
特别地,当λ=3时,三次λ-Bézier曲线将退化成经典的三次Bézier曲线。虽然形状参数的引入使曲线在形状控制手段上更加丰富,但是这种控制难以定量地讨论对几何特征的影响。
三次λ-Bézier曲线也可表示为:
p(t)=P0+[1-b0,3(t)]w1+
[b2,3(t)+b3,3(t)]w2+b3,3(t)w3
(3)
其中,wi=Pi-Pi-1=(xi,yi)(i=1,2,3)是控制多边形的边向量,并记Nij=xiyj-xjyi(i,j=1,2,3)。因此
p′(t)=-b0,3′(t)w1+[b2,3′(t)+
b3,3′(t)]w2+b3,3′(t)w3
(4)
由边向量的线性无关性易知,当4个控制点不共面时,三次λ-Bézier曲线是一条无奇点的空间曲线。以下重点讨论平面三次λ-Bézier曲线的几何形状特征。
2 三次λ-Bézier曲线的形状分析
2.1 尖点条件锥
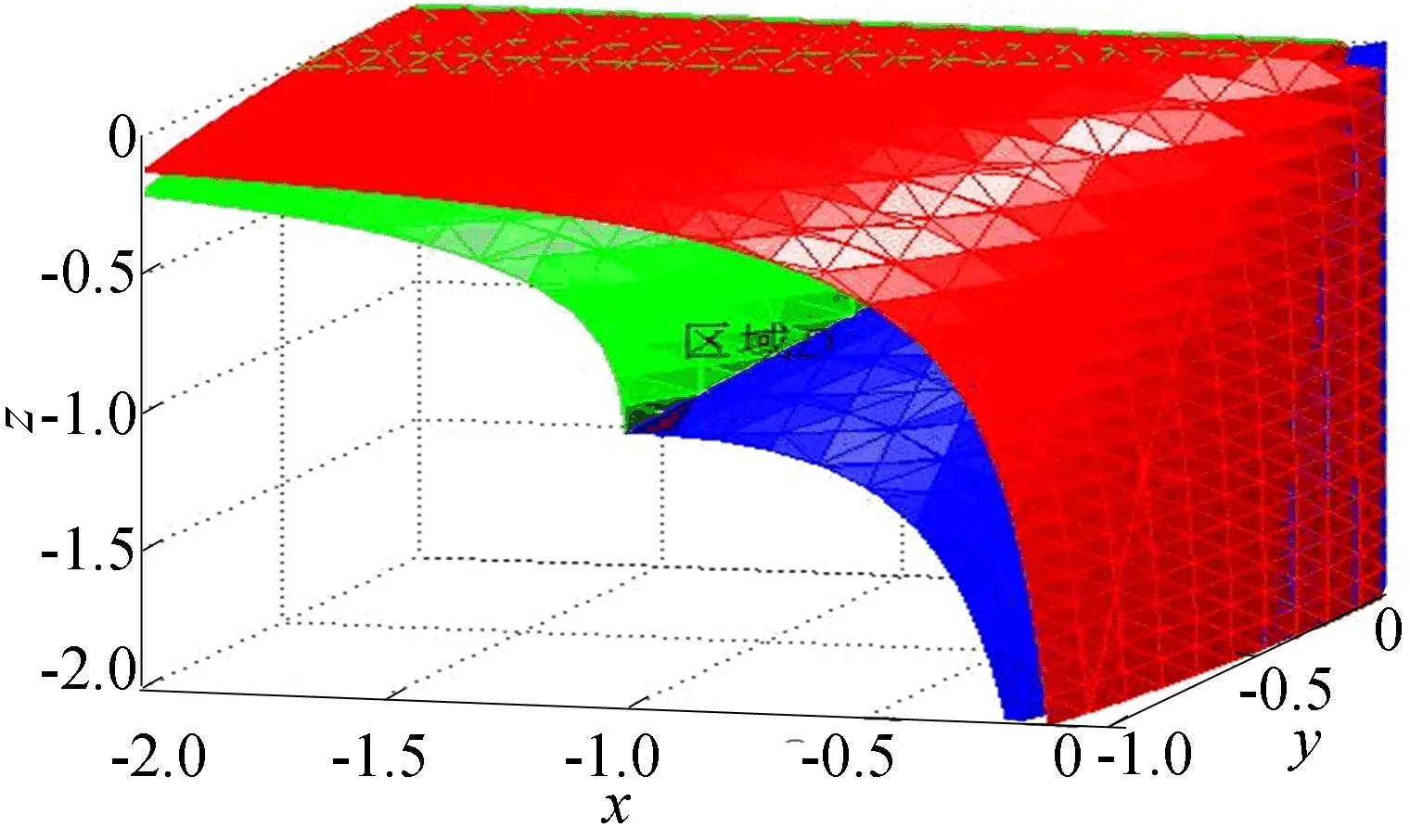
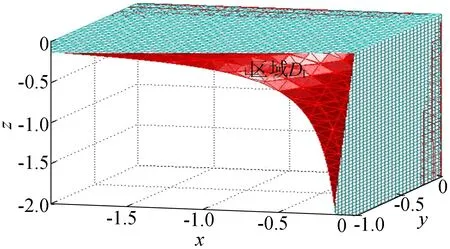
当边向量w1与w3相交,即w1×w3≠0时,可微曲线p(t)具有尖点的必要条件是p′(t)=0,0 u1w1-w2+v1w3=0, 则尖点的必要条件可表示为平面上的一条曲线,表达式为: 同理,当w1×w2≠0或w2×w3≠0时,尖点条件线可分别表示为: 或 注意到三维空间中以原点(0,0,0)为起点,分别以点(u1,-1,v1)、(u2,v2,-1)、(-1,u3,v3)为终点,形成的3个向量线性相关且互相平行,同时与向量 (x,y,z)=(-b0,3′(t),b2,3′(t)+ b3,3′(t),b3,3′(t)) (5) 平行。构造以形如(5)式的向量为母线的锥面参数方程: 即 其中,参数0 将参数方程隐式化[12],可得到其锥面方程,表达式为: FC(x,y,z)=(λ2-8λ+12)y2+ 4(λ-3)xy+4(λ-3)yz+12xz=0。 定义(x,y,z)=(N23,N31,N12)为1个特征点,因为曲线p(t)的4个控制点P0、P1、P2、P3不共线,所以(w2×w3,w3×w1,w1×w2)≠(0,0,0)。因此至少存在2个边向量不平行。假设w1与w3不平行,即w1×w3≠0。 基于尖点存在的必要条件和叶方法的讨论,可得曲线p(t)上存在尖点的另一表示形式,即存在0 (6) 因此 FC(u1,-1,v1)= (7) 同理可得: 根据锥面方程的齐次性和叉乘的可交换性ai×aj=-aj×ai,(7)式等价于 FC(N23,N31,N12)=0, 即特征点(x,y,z)=(N23,N31,N12)在尖点条件锥FC上。 反之,假设特征点在尖点锥面FC上,将特征点化简,带入锥面可得,(7)式依然成立。于是存在0 定理1 三次λ-Bézier曲线上有一尖点的充要条件是特征点在尖点条件锥FC(记为区域C)上,其中-∞ 事实上,此时曲线是全局凸的。为了方便下面的讨论,仅讨论第七卦限下的尖点条件锥FC,此时特征点的各坐标分量均小于0。 重结点是指曲线相遇的点,表示曲线上有环。曲线p(t)有重结点当且仅当存在0≤t1 (8) 因此方程(8)定义了一个拓扑映射F:Δ⊂R2→R2,像域D=F(Δ)是uv平面上的简单连通区域。区域Δ的3条边界线分别为:t1=t2,t1=0和t1=1,分别对应像域D的3条边界曲线。当边界线t1=t2时,对应尖点条件线。因此其锥面对应于尖点条件锥FC。 当t1=0时,对应p(t)-p(0)=0,即 [1-b0,3(t)]w1+[b2,3(t)+b3,3(t)]w2+ b3,3(t)w3=0, 3个边向量的系数为: (x,y,z)=(1-b0,3(t),b2,3(t)+ b3,3(t),b3,3(t))。 此时,以这些直线为母线的锥面参数方程为: 即 消参化简后,可得相应的关于端点p(0)处的重结点边界条件锥面,其方程为: F1(x,y,z)=(2-λ)y2+(λ-3)xy+ 3xz-yz-z2=0, 简记为F1,-∞ 当曲线p(t)上存在0 带入锥面方程F1有: 则有: F1(N23,N31,N12)=0。 当端点p(0)为曲线p(t)的重结点时,特征点(x,y,z)=(N23,N31,N12)在其相应的重结点边界条件锥面上,并且特征点的各分量坐标同号。 同理可得,当t1=1时,对应p(t)-p(1)=0,即 -b0,3(t)w1-[b0,3+b1,3]w2- [1-b3,3(t)]w3=0。 此时边向量的系数为: (x,y,z)=(-b0,3(t), -b0,3(t)-b1,3(t),b3,3(t)-1), 化简可得,曲线在端点p(1)处的重结点边界条件锥面(简记为F2)的方程为: F2(x,y,z)=(λ-2)y2+ (3-λ)yz-3xz+xy+x2=0, 其中,-∞ 图1 第七卦限的重结点区域 定理2 三次λ-Bézier曲线存在重结点的充要条件是特征点(x,y,z)=(N23,N31,N12)在FC与F1和F2所构成的空间区域D内(图1中绿色与蓝色区域内)。 注意如下2点:① 此时的空间区域包含重结点边界条件锥面F1和F2;② 特征空间是指被FC与F1和F2,以及其相应的切平面,划分成多个不同区域的三维空间。其中,每一特征区域对应该曲线不同形状特征。 进一步分析可得尖点锥FC与重结点边界锥F1和F2的交线τ1和τ2,即 因此,尖点锥FC在交线τ1和τ2处的切平面分别为: c1:z=0 和c2:x=0。 τ12:x=y=z是重结点边界锥F1和F2的交线。同理可得,F1和F2在交线τ12处的切平面分别为: π1:x-y=0,π2:x-z=0。 显然,切平面π1过尖点锥FC和F2的交线τ2和公切线τ12;切平面π2过尖点锥FC和F1的交线τ1和公切线τ12。 事实上,当参数λ=3时,用平面x+z+1=0切割3张特征锥面,由FC(红色曲面)与F1(蓝色曲面)和F2(绿色曲面)构成的特征空间时,所得的特征空间截面图如图2所示。图2揭示了3张特征锥面的各截面线之间的对应关系,与文献[5]所讨论的形状条件分布图类似,且进一步统一了文献[5]对形状条件分布图分类讨论的情况。 图2 平面三次λ-Bézier曲线特征空间截面 点p(t0)是否是曲线p(t)的拐点,可由P′(t)×P″(t)通过t0时的符号是否发生变化判断,而 因此,曲线p(t)存在拐点当且仅当特征点(x,y,z)=(N23,N31,N12)在下列方程表示的平面上。 (9) 注意到方程(9)的系数是锥面FC在参数t处的法向量,因此基于文献[5]的分析得知,FC的切平面扫过的区域即为该曲线可能的拐点区域。进一步计算得知,尖点锥FC在交线τ1和τ2处的切平面即为FC在其边界处的切平面c1和c2。当特征点位于尖点锥面及其边界切平面所构成的空间区域时,过其可做FC的2张切平面,对应于曲线存在的2个拐点。否则,尖点锥FC仅存在1张切平面,对应曲线存在1个拐点。第七卦限的双拐点区域如图3所示。类似尖点与重结点的讨论,有如下定理。 定理3 当特征点(N23,N31,N12)在尖点锥FC与切平面c1:z=0和c2:x=0构成的范围内时(图3不包含边界),在尖点锥FC上过该特征点存在2张切平面,此时区域DI(红色区域)为双拐点区域。否则,对应的是曲线p(t)的单拐点区域,记为SI。 图3 第七卦限的双拐点区域 从定理3可得,拐点区域与尖点锥FC的包络关系与叶方法的讨论一致。 为了便于描述,记 N=R2(C∪SI∪DI∪D), 此时曲线p(t)上不存在奇点(尖点和重结点)和拐点,且法向量p′(t)×p″(t)的方向不变。考虑 m(t)=P′(t)×[P(1)-P(t)]= n(t)=[P(t)-P(0)]×P′(t)= 由于b0,3+b1,3+b2,3+b3,3=1,b0,3′+b1,3′+b2,3′+b3,3′=0,化简可得: m(t)=m23(w2×w3)+ m03(w3×w1)+m01(w1×w2), n(t)=n23(w2×w3)+ n03(w3×w1)+n01(w1×w2)。 其中 经过进一步推导得出,F2在t处的法向量为{m23,m03,m01},即条件锥F2是m(t)变号区域的包络面。 特别地,规定N1为锥面F2的切平面π2在N中覆盖的区域,此时曲线p(t)在锥面F1与切平面π2围成的区域内是局部凸的。由于锥面F1是n(t)变号区域的包络面,规定N2为锥面F1的切平面π1在N中覆盖的区域,此时曲线p(t)在F2与π1围成的区域内也是局部凸的;否则曲线p(t)是全局凸的。将N中尚未被讨论的区域记为区域N0。 定理4 当特征点(N23,N31,N12)位于N=N1∪N2(图4中蓝色区域与绿色区域)区域内(不包括边界)时,曲线p(t)是局部凸的;否则,曲线p(t)是全局凸的。 图4 第七卦限的局部凸区域 分别用平面y=-1,z=-1及x=-1切割构造的特征空间,所得的截面图如图5所示。图5正好对应基于叶方法所得的3种形状条件分布图。 图5 三次λ-Bézier曲线特征空间截面图 图5a~图5c分别对应叶方法中的w1×w3≠0、w1×w2≠0、w2×w3≠0的情况。图5中:红色曲面均表示FC,绿色曲面表示F1,蓝色曲面表示F2;2张白色平面分别表示F1和F2在交线τ12处的切平面π1和π2;青绿色平面表示相应的切割平面。 由于各锥面方程和曲线p(t)具有对称性,曲线的形状不会因控制顶点的位置取反而改变。因此,各特征区域具有对称性,但此时特征点(x,y,z)=(N23,N31,N12)各分量的符号发生改变。由于特征空间的对称性质,为简化特征点位置判断的计算,将特征空间限制在下半空间z≤0即可。 为进一步研究形状参数λ对曲线p(t)特征空间的影响,用平面x+z+1=0切割特征空间所得的截面图,如图6所示。显然,随着λ的增大,各特征锥面均呈现膨胀趋势。因此,双拐点区域DI、重结点区域D和局部凸区域N均呈扩大趋势,相应地,单拐点区域SI逐渐缩小。因为锥面F1和F2在其交线处的切平面方程与参数λ无关,所以参数λ值的改变对曲线p(t)的全局凸区域N0不产生影响,但可通过调节参数λ使p(t)成为全局凸,但不可能为局部凸曲线。 图6 形状参数λ对平面三次λ-Bézier曲线特征空间的影响 通过调节形状参数λ,改变各锥面方程的具体表达,从而对各特征区域进行压缩与放大,进而调节参数曲线的特征空间分布。 本文利用特征空间法对三次λ-Bézier曲线的形状进行研究分析。通过对参数方程进行隐式化,构造与尖点条件线和重结点条件线相应的含参特征锥面,并计算出各锥面的切平面。虽然各锥面方程在结构上与原有Bézier曲线类似,但是参数λ的引入,使得该曲线获得一定的形状调节能力。 利用各锥面与其切平面构成的特征空间分布,得到尖点区域、重结点区域、拐点区域和凸性区域;曲线的形状特征由特征点在特征空间的区域位置决定。该方法统一了文献[8]和文献[9]讨论的情况,简化了计算,有利于计算机的交互设计;分析了形状参数λ对各特征锥面和特征空间的影响,通过调节参数,可以获得工业设计所需的几何形状。2.2 重结点边界条件锥
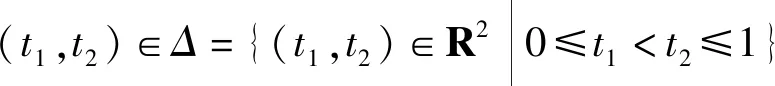
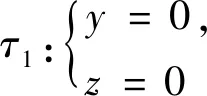

2.3 拐点区域
2.4 凸性区域

3 三次参数λ对曲线特征空间的影响

4 结 论

