强Prüfer环上的半正则平坦模

张晓磊, 戴国成, 肖雪莲, 齐 薇

(1. 山东理工大学 数学与统计学院, 山东 淄博 255049; 2. 四川师范大学 数学科学学院, 成都 610066;3. 阿坝师范学院 数学学院, 四川 汶川 623002)

本文设R是有单位元的交换环,T(R)是R的完全商环.根据文献[1]: 环R的理想I称为稠密理想是指理想(0:RI)={r∈R|Ir=0}=0; 如果理想I包含一个有限生成稠密子理想, 则称I是半正则理想; 环R的理想I称为正则理想是指I中至少存在一个正则元素.设I是R的理想, 记I-1={z∈T(R)|Iz⊆R}.如果环R的理想I满足II-1=R, 则I称为可逆理想.

有限生成非零理想都是可逆的整环, 称为Prüfer整环[2]. 文献[3]给出了Prüfer整环的系统总结. 由于Prüfer整环在环论研究中具有重要意义, 因此备受关注, 目前已将Prüfer整环推广到一般交换环上. Butts等[4]给出了Prüfer环的概念, 即有限生成正则理想都是可逆理想的环; Griffin[5]利用乘法理想理论给出了Prüfer环的等价刻画; 肖雪莲等[6]从模论的角度研究Prüfer环, 给出了Prüfer环的等价刻画.

由于Prüfer环定义较简单, 很难进行更深入的研究. 因此, 为更多了解Prüfer环, 文献[7]引入了强Prüfer环的概念, 即有限生成半正则理想都是局部主理想的环, 并证明了环R是强Prüfer环当且仅当其Nagata环R(x)是Prüfer环; 文献[8]从有限生成半正则理想格论的角度刻画了强Prüfer环, 例如环R是强Prüfer环当且仅当R的所有有限生成半正则理想构成的格Lsr(R)是分配格; 文献[9]证明了环R是强Prüfer环当且仅当R是Prüfer环, 且T(R)是强Prüfer环. 强Prüfer环也与环的小finitistic维数密切相关. 环R的小finitistic维数fPD(R)定义为

fPD(R)=sup{pdRM|M是超有限表现模, pdRM<∞},

这里超有限表现模是指存在有限生成的投射分解的模.文献[10]证明了环R满足fPD(R)=0当且仅当R是DQ(identity quotient)环, 即有限生成半正则理想只有R的环; 文献[11]证明了连通的强Prüfer环R满足fPD(R)≤1; 文献[12]证明了任意强Prüfer环R的fPD(R)≤1, 并且通过实例说明对任意的n∈, 均存在Prüfer环R满足fPD(R)=n.

本文主要从模论和同调理论的角度研究强Prüfer环. 首先, 研究半正则平坦模、 半正则余平坦模和半正则余挠模, 并证明半正则平坦模类和半正则余挠模类构成了完全的余挠理论; 其次, 利用半正则平坦模、 半正则余平坦模和半正则余挠模给出DQ环的等价刻画以及强Prüfer环的等价刻画, 即证明R是强Prüfer环当且仅当半正则平坦模的任意子模都是半正则平坦模, 当且仅当环R的任意有限生成理想都是半正则平坦模, 当且仅当半正则余平坦模的任意商模都是半正则余平坦模， 当且仅当h-可除模都是半正则余平坦模; 最后, 给出半正则凝聚环的相关刻画, 并证明R是强Prüfer环当且仅当任意R-模均有满的半正则平坦包, 当且仅当任意R-模均有满的半正则平坦预包.

1 余挠理论

显然, 任意平坦模都是半正则平坦模, 任意半正则平坦模都是正则平坦模.对偶地, 可以给出半正则余平坦模的概念.

引理1设M是R-模, 则下列叙述等价:

1)M是半正则平坦模;

2) 对任意有限生成半正则理想I, 自然同态I⊗M→R→R⊗M是单同态;

3) 对任意有限生成半正则理想I, 自然同态σI:I⊗M→IM是同构;

4) 对任意内射模E, HomR(M,E)是半正则余平坦模;

5) 若E是内射余生成子, 则HomR(M,E)是半正则余平坦模.

证明: 1)⟺2).设I是有限生成半正则理想, 则有长正合列

2)⟹3).设I是有限生成半正则理想, 则有如下交换图:

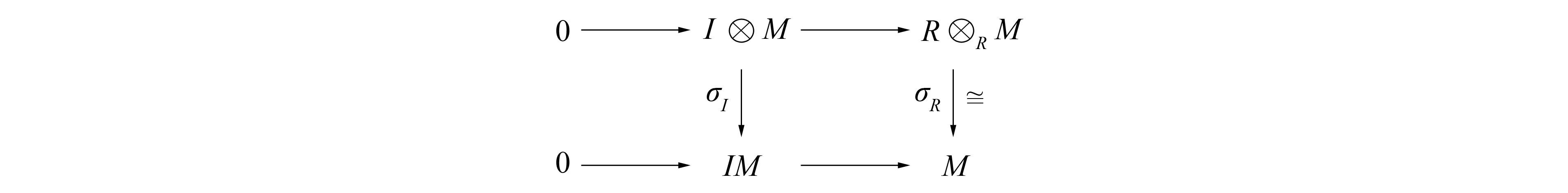
从而σI是单同态.显然乘法同态σI是满同态, 所以σI是同构.

3)⟹1).设I是有限生成半正则理想, 由3)有如下长正合列:

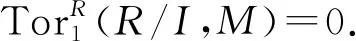
1)⟹4).设I是有限生成半正则理想,E是内射模, 则有

(1)

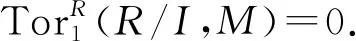
4)⟹5)显然成立.

引理2设R是环, 则半正则平坦模类Fsr关于正向极限、 纯子模和纯商模封闭.

证明: 对于正向极限, 设{Mi}i∈Γ是半正则平坦模构成的正向系统.则对任意有限生成半正则理想I,

对于纯子模和纯商模, 设f: 0→I→R→R/I→0是短正合列, 其中I是有限生成的半正则理想, 0→M→N→L→0是R-模的纯正合列, 则可得如下正合列交换图：

由蛇形引理知, 自然同态f:M⊗RI→M⊗RR和g:L⊗RI→L⊗RR都是单同态, 从而M,L都是半正则平坦模.证毕.

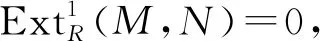
显然, 任意内射模都是半正则余挠模, 任意半正则余挠模都是余挠模.由文献[13]可知, 平坦模类和余挠模类组成一对完全的余挠理论.下面证明半正则平坦模类和半正则余挠模类也组成一对完全的余挠理论.

定理1设R是环, 则 (Fsr,Csr)是完全的余挠理论.从而半正则平坦模类Fsr是盖类, 半正则余挠模类Csr是包类.

证明: 显然R是半正则平坦模, 并且半正则F关于扩张和直和项封闭.由引理2和文献[14]中定理3.4可得(Fsr,Csr)是平坦余挠理论.因此, 半正则平坦模类Fsr是盖类, 半正则余挠模类Csr是包类.证毕.

命题1设R是环, 则下列叙述等价:

1)M是半正则余挠模;

2) 对于任意平坦模F, HomR(F,M)是半正则余挠模;

3) 对于任意投射模P, HomR(P,M)是半正则余挠模.

证明: 1)⟹2).设N是半正则平坦模,F是平坦模.则由短正合列0→K→P→N→0, 可得短正合列

0→K⊗RF→P⊗RF→N⊗RF→0，

其中P为投射R-模.因为对任意有限生成半正则理想I均有

故有N⊗RF是半正则平坦R-模.由于

正合, 从而有短正合列

HomR(P,HomR(F,M))→HomR(K,HomR(F,M))→0.

此外,

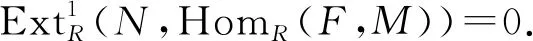
2)⟹3)显然.

3)⟹1).只需设P=R即可得结论.证毕.

2 同调理论

由文献[10]中命题2.2知, 环R是DQ环当且仅当R的有限生成半正则理想只有R.如果任意R-模都是平坦R-模, 则环R称为VN(von Neumann)-正则环.下面给出任意R-模都是半正则平坦模的等价刻画.

定理2设R是环, 则下列叙述等价:

1)R是DQ环;

2) fPD(R)=0;

3) 任意R-模都是半正则平坦模;

4) 任意R-模都是半正则余平坦模;

5) 任意半正则余挠模都是内射模;

6) 对任意有限生成理想J和有限生成半正则理想I, 均有I∩J=IJ;

7) 对任意有限生成半正则理想I,R/I是平坦模;

8) 对任意有限生成半正则理想I和a∈I, 均有c∈I使得(1-c)a=0.

证明: 1)⟹3), 1)⟹4)和1)⟹7)显然.1)⟺2)参见文献[10]中命题2.2.3)⟺5)由定理1可得.6)⟺7)⟺8)参见文献[15]中定理1.2.15.

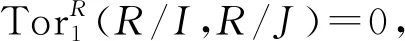
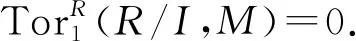
4)⟹1).设I是任意有限生成半正则理想, 则由4)可知R/I是投射模, 从而I是有限生成幂等理想.由文献[16]中命题1.10知,I=〈e〉, 其中e是幂等元.从而1-e∈(0:RI)=0, 于是I=R.证毕.

下面给出非平坦的半正则平坦R-模和非半正则的正则平坦模实例.

例1设R是非域的零维Noetherian局部环.根据文献[17],R满足fPD(R)=0.由于R是非域的局部环, 故R不是VN-正则环.根据定理2知, 存在非平坦的半正则平坦R-模.

例2由文献[6]中定理2.13知,R是全商环当且仅当任意R-模都是正则平坦模.文献[18]给出了满足fPD(R)>0的全商环的实例.从而存在正则平坦模不是半正则平坦模.

推论1设R是环, 则下列叙述等价:

1)R是半单环;

2) 任意半正则平坦模是投射模;

3) 任意R-模都是半正则余挠模.

证明: 1)⟹2)和1)⟹3)显然.

2)⟹1).由2)可知平坦模都是投射模.故R是完全环, 即FPD(R)=0, 从而fPD(R)=0, 其中FPD(R)是指环R的大finitistic维数.由定理2可知任意R-模都是半正则平坦模, 故都是投射模.因此R是半单环.

2)⟺3).由定理1可得.证毕.

若M是一个内射模的商模, 则R-模M称为h-可除模.

定理3设R是环, 则下列叙述等价:

1)R是强Prüfer环;

2) 半正则平坦模的任意子模都是半正则平坦模;

3) 平坦模的任意子模都是半正则平坦模;

4) 环R的任意理想都是半正则平坦模;

5) 环R的任意有限生成理想都是半正则平坦模;

6) 环R的任意有限生成半正则理想都是平坦模;

7) 环R的任意有限生成半正则理想都是投射模;

8) 半正则余平坦模的任意商模都是半正则余平坦模;

9)h-可除模都是半正则余平坦模.

证明: 2)⟹3)⟹4)⟹5), 7)⟹6)和8)⟹9)显然.

5)⟺6).设I是任意有限生成半正则理想,J是任意有限生成理想, 则有如下短正合列:

0→I→R→R/I→0, 0→J→R→R/J→0.

从而可得

进而J是半正则平坦模当且仅当I是平坦模.

6)⟹1).设I是有限生成半正则理想,m是R的极大理想, 则Im是有限生成平坦Rm-理想.由文献[15]中引理4.2.1及文献[19]中定理2.5可知,Im是自由Rm-理想.故rank(Im)≤1, 从而Im是Rm的主理想.

1)⟹6).设I是有限生成半正则理想,m是R的极大理想, 则Im是局部主的Rm-理想.设Im=〈x/s〉, 则由文献[1]可得

6)⟹2).设M是半正则平坦模,N是M的子模.设I是任意有限生成半正则理想, 则I是平坦理想, 从而fdR(R/I)≤1.考虑长正合列

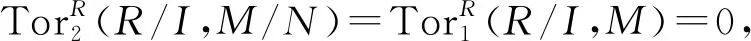
6)⟹7).由文献[20]中推论3.1可得.

9)⟹7).设I是有限生成半正则理想,M是R-模.考虑短正合列0→M→E→N→0, 其中E是内射模, 则N是h-可除模.从而

因此I是投射理想.

7)⟹8).设I是有限生成半正则理想, 则I是投射理想, 从而pdR(R/I)≤1.设0→L→M→N→0是短正合列, 其中M是半正则余平坦模, 则有

3 半正则凝聚环

任意有限生成理想都是有限表现理想的环称为凝聚环. 例如Noether环和Prüfer整环等. 但强Prüfer环不一定是凝聚环. 为此, 本文引入半正则凝聚环的概念, 并通过(预)包类给出强Prüfer环新的刻画.

定义4任意有限生成半正则理想I都是有限表现理想的环称为半正则凝聚环.

设R是非半遗传弱总体维数为1的环, 则R是强Prüfer环, 但不是凝聚环[15]. 下列命题表明任意强Prüfer环必为半正则凝聚环.

命题2设R是强Prüfer环, 则R是半正则凝聚环.

证明: 设I是R的有限生成半正则理想, 则由定理3可知I是投射理想, 从而是有限表现理想.证毕.

许多非整环的实例都是通过理想化R(+)M构造的, 其中M是R-模[21].令R(+)M作为R-模同构于R⊕M, 定义

(r,m)+(s,n)=(r+s,m+n),

(2)

(r,m)(s,n)=(rs,sm+rn).

(3)

在上述定义下,R(+)M成为有单位元(1,0)的交换环.下面利用理想化构造方法给出半正则凝聚环的实例.

命题3设D是凝聚整环,K是D的商域.令R=D(+)K, 则R是半正则凝聚环.此外,R是凝聚环当且仅当D是域.

证明: 根据文献[22]中注1知,R是强φ-环, 所以Nil(R)=0(+)K, 且任意R-理想均可与Nil(R)比较.从而由文献[23]中推论3.4可知,R的理想均形如I(+)K或0(+)L, 其中I是D的非零理想,L是K的D-子模.若I是D的非零理想, 则显然I(+)K是R的半正则理想.若I(+)K是有限生成理想, 不妨设I(+)K由{(d1,x1),(d2,x2),…,(dn,xn)}生成, 则易证I由{d1,d2,…,dn}生成.因为R是凝聚环, 所以存在D-模短正合列Dm→Dn→I→0.由于R是平坦D-模, 故张量R得到D-模正合列Rm→Rn→I(+)K→0.易验证该正合列也是R-模正合列.从而I(+)K是有限表现R-理想.显然, 有限生成R-理想0(+)L中的元素都是幂零元素, 从而不是半正则理想.所以R是半正则凝聚环.

显然若D是域, 则R是凝聚环.下面说明若D不是域, 则R不是凝聚环.注意到(0,1)R是有限生成R-理想.考虑自然短正合列0→L→R→(0,1)R→0, 则L=Nil(R)=0(+)K.由于D不是域, 所以K不是有限生成D-模, 从而不是有限生成D-模.由文献[24]中引理2.2可知, 理想Nil(R)不是有限生成R-理想, 从而(0,1)R不是有限表现的.证毕.

定理4对于环R, 下列叙述等价:

1)R是半正则凝聚环;

2) 半正则平坦模的直积是半正则平坦模;

3) 平坦模的直积是半正则平坦模;

4)R的直积是半正则平坦模;

5) 半正则余平坦模的直向极限还是半正则余平坦模;

6) 半正则余平坦模关于纯商模封闭;

7) 半正则余平坦模是预盖类;

8) 半正则余平坦模是盖类;

9) 对于任意半正则余平坦模N, 内射模E均有HomR(N,E)是半正则平坦模;

10) 若E是内射余生成子, 则对任意半正则余平坦模N均有HomR(N,E)是半正则平坦模;

11) 对任意半正则平坦模M, 内射模E1和E2均有HomR(HomR(M,E1),E2)是半正则平坦模;

12) 若E1和E2是内射余生成子, 则对任意半正则平坦模M均有HomR(HomR(M,E1),E2)是半正则平坦模.

证明: 2)⟹3)⟹4)显然成立.

1)⟹2).设I是有限生成半正则理想, {Fi}i∈I是一族半正则平坦模构成的集合.考虑如下交换图:

4)⟹1).设I是有限生成半正则理想, 考虑如下交换图：

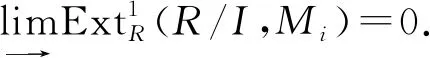
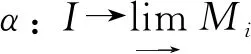
5)⟺6)⟺7)⟺8).根据文献[26]中引理3.4可得.

1)⟹9).设I是有限生成半正则理想,E是内射模,N是半正则余平坦模.考虑短正合列0→I→R→R/I→0, 则有如下正合列交换图(用(-,-)代替HomR(-,-)):

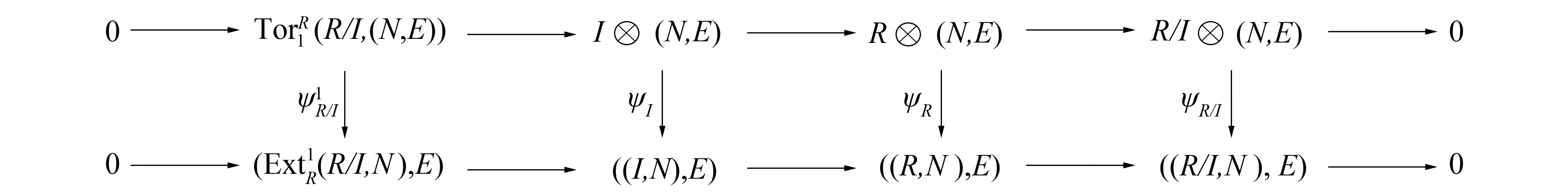
9)⟹10)和11)⟹12)显然成立.9)⟺11)和10)⟺12)根据定理1可得.

10)⟹1).设I是有限生成半正则理想,N是半正则余平坦模,E是内射余生成子, 则有如下交换图:

由10)可知f是单态射, 故ψI是单态射, 从而由文献[27]中命题8.14(1)可知,I是{R}-Mittag-Leffler模.又因为I是有限生成理想, 故根据文献[25]中定理2可知I是有限表现理想.证毕.

引理3设R是环, 则R是半正则凝聚环当且仅当半正则平坦模类Fsr是预包类.

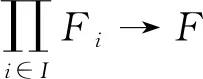
推论2设环R是半正则凝聚环, 且半正则平坦模类Fsr关于反向极限封闭, 则Fsr是包类.

证明: 由引理3可知得半正则平坦模类F是预包类, 从而由文献[28]中推论6.3.5可知Fsr是包类.证毕.

引理4[29]设F是关于子模封闭的R-模类,f:M→F是F-包, 则f是满射.

引理4给出了关于子模封闭模类包的性质.作为应用, 可得下列结论.

定理5设R是环, 则下列叙述等价:

1)R是强Prüfer环;

2) 任意R-模均有满的半正则平坦包;

3) 任意R-模均有满的半正则平坦预包.

证明: 2)⟹3)显然.