轴力作用下多点约束杆件的横向振动及稳定简化分析方法

陈飘华，张慧健，黄仕平,2，袁兆勋

(1.华南理工大学 土木与交通学院，广州 510640；2.中新国际联合研究院，广州 510700)

在实际工程中，结构构件及许多机械设备都是在承受轴向荷载的情况下工作，例如受拉的缆索、桁架拱的受压腹杆等。当轴向压力超过某一临界压力时，压杆将丧失保持稳定平衡构形的能力从而发生屈曲或失稳[1]。根据结构动力学[2]可知，杆件在承受压力时，频率会有所降低，且压力越大，频率降低越多。结构振动频率作为结构动力特性的重要指标，是结构动力分析及控制的重要参数，因此轴力条件下杆件的自由振动引起了众多学者研究。Huang等[3]提出一种动态有限元单元法用于计算斜拉索的振动频率与索力。孙秀荣等[4]研究了一端固定一端滑动下分布轴向力对杆柱失稳和横向振动的影响。李梦瑶[5]研究了简支箱梁在剪力滞效应和附加轴力影响下的自由振动特性。滕兆春等[6]研究了轴向力对一端固定一端滑动梁的过屈曲前后固有频率的影响。楼梦麟等[7]采用模态摄动法分析了预应力对简支梁横向振动特性的影响。陈永红等[8]研究了轴向运动Timoshenko梁在轴向载荷作用下的振动特性。赵雨皓等[9]建立了轴向载荷条件下弹性边界约束梁结构的振动分析模型。

上述研究大多是基于特定端部支承条件下轴力对自由振动影响的研究，且在实际工程中，为了改善构件的动力性能，通常会在构件的中间设置附加约束条件来控制其振动频率，例如受拉缆索为了增加刚度，在其中部设置附加约束；钢结构中为提高钢梁的整体稳定性，通常在其受压翼缘处设置侧向支承点。合理设置附加支承可以控制构件的振动频率及欧拉临界力，提高构件的动力性能及稳定性，保证其在振动过程中不发生破坏或者失效。对于含中间支承的研究，吴晓[10]利用Laplace变换求得了多跨连续长索固有横振振型的解析解。黄翀等[11]研究了多跨索支承在同一平面且不在同一直线上的固有振动特性。荆洪英等[12]研究了一端固支且自由端轴向受压具有中间支承梁的横向振动特性。Xiao等[13]基于Mindlin-Goodman法和模态叠加法，分析了轴力作用下均匀Euler-Bernoulli梁在随机支承激励下的动响应。

综上所述，轴力下含附加约束杆件的振动频率较为复杂，一般采用有限单元法等数值方法进行计算，然而有限单元法需要软件建模且不够直观。基于此，本文采用特征函数集和相应的特征值建立基本结构的势能泛函方程，利用拉格朗日乘子法考虑泛函中的附加约束条件，推导在不同端部支承方式下轴力作用杆件在多点约束下的频率计算公式，并根据频率和轴力之间的关系得到该杆件的欧拉临界力，为结构设计及计算提供简便的计算公式。

1 多点约束下梁的频率公式推导

本章先建立轴向荷载下梁的总势能泛函，然后通过拉格朗日乘子法考虑附加约束，最后通过最小势能原理求解振动频率及相应的欧拉临界荷载。

取梁上任一截面x处的微段dx为隔离体，该微段有作用在两个截面上的弯矩M，剪力Q，轴力N及分布惯性力m(x)(∂2y/∂t2)，如图1所示。

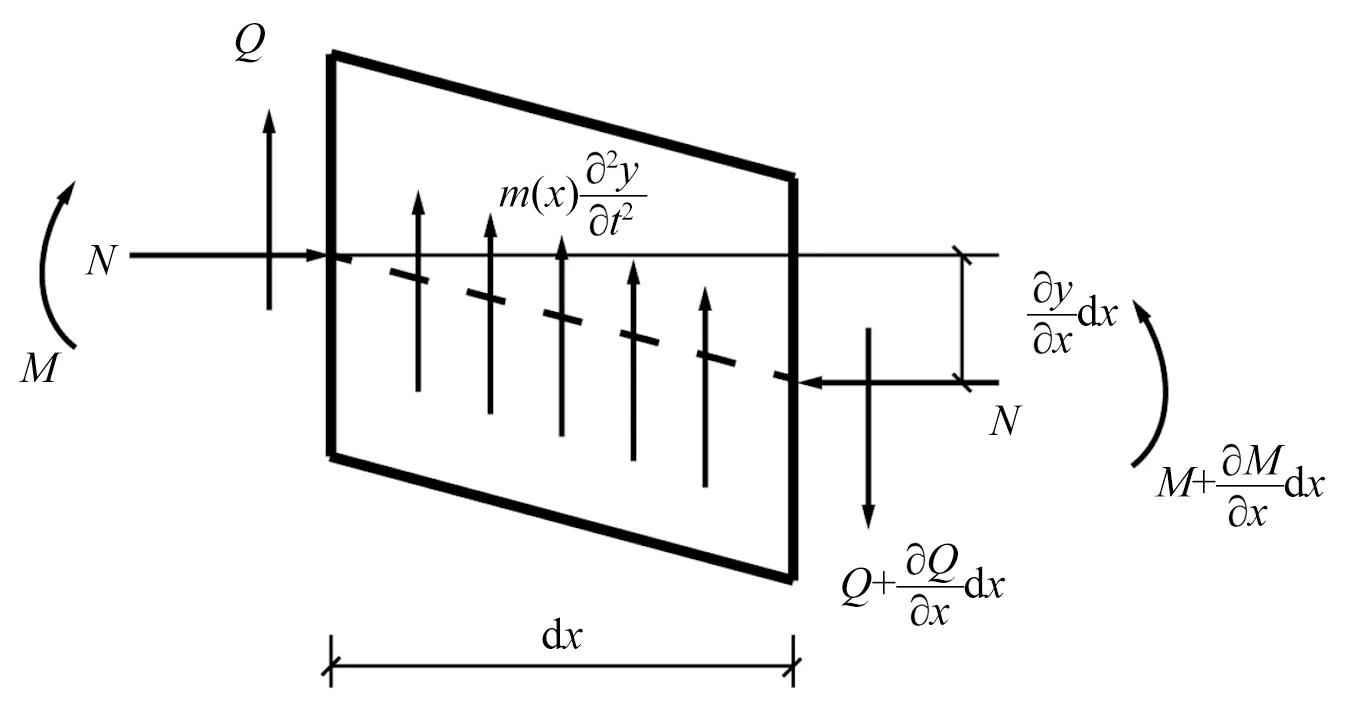
图1 梁段隔离体Fig.1 Beam segment isolation body

由梁段隔离体的力及力矩平衡方程求得轴向力作用下欧拉梁的横向振动方程

(1)

式中：E为梁的弹性模量；I(x)为梁的惯性矩；y为梁的横向位移；x为梁的坐标；m(x)为梁的单位长度质量；N为梁受到的轴向力。

假定梁遵循简谐振动，则梁的挠度y可以分离成时间和空间变量

y=Y(x)sin(ωt+φ)

(2)

式中：ω为角速度，(rad/s)；φ为相位角。

将式(2)代入式(1)中可以得到

(3)

给定梁端的边界条件(如简支、固支或自由)，则会有相应的一组封闭的特征函数φr(x)和特征值λr=ω2对应梁的第r阶振型。其特征函数有如下特性

(4)

满足边界条件的梁振动模态可以看作是各阶特征函数φr(x)的叠加

无阻尼作用下梁振动的总势能在任何时刻都是相同的，因此我们考虑梁在最大挠度位置处时的势能。梁的最大挠度可以表示为

Y(x)=a1φ1(x)+a2φ2(x)+a3φ3(x)+…

(6)

梁在最大挠度位置处的应变能

(7)

对式(7)进行分部积分

当梁端为简支或自由时，梁端弯矩EI(x)(d2Y/dx2)为0；当梁端为固支时，梁端转角dY/dx为0，故式(8)简化成

(9)

对式(9)再次进行分部积分

同理，当梁端为简支或固支时，梁端挠度Y为0；梁端为自由时，梁端剪力(d/dx)[EI(x)(d2Y/dx2)]为0，故应变能最终简化成

(11)

将式(3)代入式(11)中

(12)

同时，梁的势能

(13)

当梁的两端之间x=c1,c2,c3，…处有n个附加约束，如图2所示。

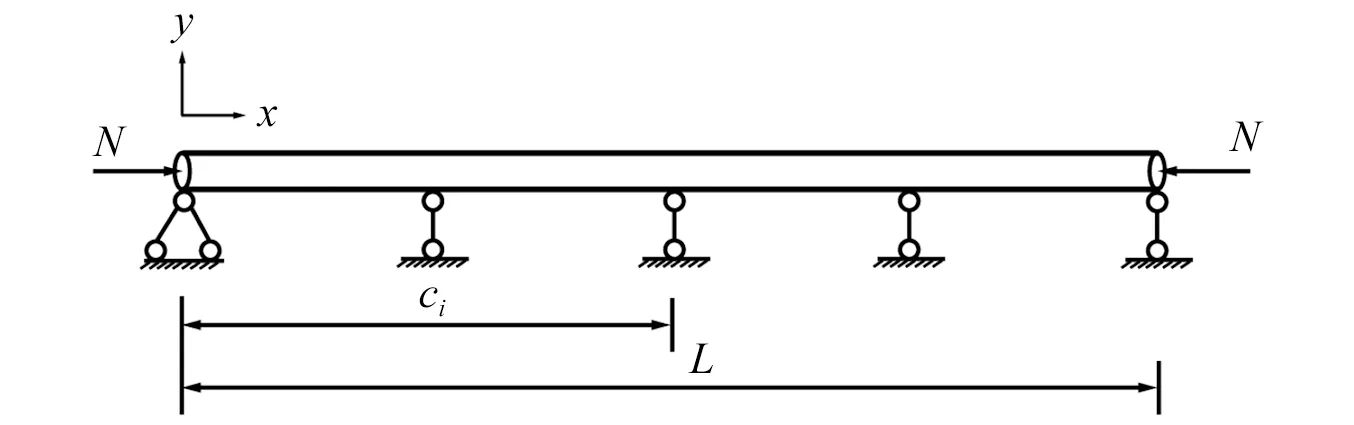
图2 轴向荷载下多点约束梁结构振动模型Fig.2 Vibration model of multi-point restrained beam structure under axial force

ci处对应的位移Yci

Yci=a1φ1(ci)+a2φ2(ci)+a3φ3(ci)+…

(14)

同时在梁的总势能公式中引入n个拉格朗日乘子法[14]变量μ1,μ2,μ3…，则其总势能泛函П为[15]

(15)

式中:U为应变能由式(12)求出;V为势能由式(13)求出。

根据最小势能原理，总势能П需要满足以下条件

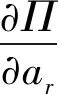
(16)

和附加约束条件

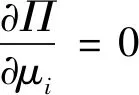
将式(15)代入式(16)得到ar后，再将ar代入式(17)即可得到梁在多点约束下的频率计算公式。

梁承受压力时，其自振频率会有所减小，相当于降低了梁的刚度，当梁的一阶频率降为零时，结构会发生失稳，此时的压力即为欧拉临界力。因此，当频率公式中λ为0时，所得到的轴力N即为结构的欧拉临界力。

本方法对任意端部支承方式的杆件都适用，只要知道其特征函数即可求解相应的频率公式及欧拉临界力。1.1节以端部支承为简支和固支为例，求其振动频率及相应的欧拉临界力。

1.1 等截面简支梁在多点约束下的频率公式

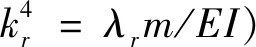
(18)

根据式(18)，将特征函数代入式(12)和式(13)可得简支梁的应变能和势能

(20)

则总势能П

当两端之间x=c1处只有一个附加约束时(即n=1)，根据最小势能原理，将总势能代入式(16)可得

(22)

再将式(22)代入式(17)可得简支梁在单点约束下的振动频率公式

(23)

当式(23)中λ=0且r=2时，可得简支梁在单点约束下的欧拉临界力

(24)

当两端之间x=c1，c2处有两个附加约束时(即n=2)，根据最小势能原理，将总势能代入式(16)可得

(25)

再将式(25)代入式(17)整理可得

(26)

式(26)有非零解的必要条件是μ1，μ2的系数行列式为零，可得简支梁在两点约束下的振动频率公式

同理，对式(27)取λ=0且r=3时，可得简支梁在两点约束下的欧拉临界力

(28)

式中:A=[φ1(c1)φ2(c2)-φ2(c1)φ1(c2)]2；B=[φ1(c1)φ3(c2)-φ3(c1)φ1(c2)]2；C=[φ2(c1)φ3(c2)-φ3(c1)φ2(c2)]2。

1.2 等截面固支梁在多点约束下的频率公式

固支梁的特征函数为

φr(x)=cosh(krx)-cos(krx)+γr[sinh(krx)-sin(krx)](29)

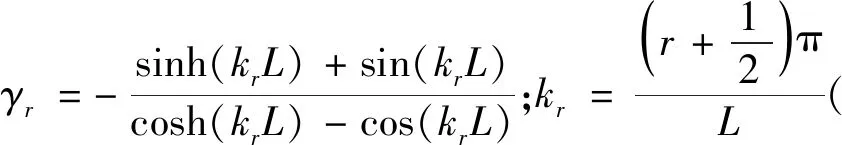
则固支梁特征函数有如下特性

(30)

因篇幅有限，本文仅给出固支梁在单点约束(即x=c1处)下的基频计算公式，因此对固支梁特征函数仅取前两项，则根据式(12)和式(13)可得固支梁的应变能和势能

(31)

(32)

则总势能П

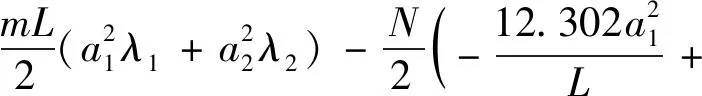
μ1[a1φ1(c1)+a2φ2(c1)]

(33)

同样总势能П需要满足式(16)和式(17)

(34)

同理，对上述式(34)消除a1和a2，即可得固支梁在单点约束下的基频。若要求出前r阶频率，则特征函数需要取前r+1项计算。

实际工程中考虑到制造、施工、造价和外观等因素，一般约束数量有限，大多在3个以内。对于大部分对称结构，当约束较多时，可通过取半结构的方法对约束数量进行简化。

2 实例及验证

2.1 简支梁在单点约束下的频率

以两端简支且轴向受拉的拉索为例，拉索长度12 m，圆形截面采用直径7.3 cm，附加约束位于跨距比l1∶l2=5∶7处。有限元模型采用一维梁单元且等间距划分单元，梁端边界为铰接，中间支承仅约束竖向位移，具体参数如图3、表1所示。

图3 拉索结构示意图Fig.3 Schematic diagram of cable structure

表1 拉索模型的材料参数Tab.1 Material parameters of cable model

将拉索尺寸及材料参数代入式(23)，并对该式取前7项(即r=7)可得拉索的前6阶频率，计算结果与有限元模型对比，如表2所示。前6阶频率的最大误差不足3%，满足工程计算需求。

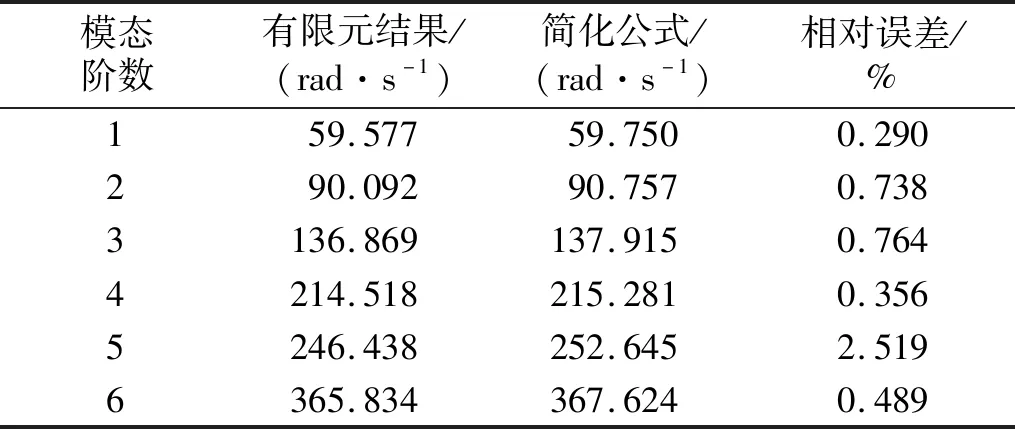
表2 前6阶频率对比Tab.2 Comparison of the first six frequencies

2.2 简支梁在两点约束下的频率

以两端简支且轴向受压的钢梁为例，钢梁长度10 m，截面采用HW 200×200×8/12，附加约束位于跨距比l1∶l2∶l3=3∶4∶3处。有限元建模方式与上述拉索相同，具体参数如图4、表3所示。

图4 钢梁结构示意图Fig.4 Schematic diagram of steel beam structure

表3 钢梁模型的材料参数Tab.3 Material parameters of steel beam model

将钢梁尺寸及材料参数代入式(27)中，并对该式取前8项(即r=8)可得钢梁的前六阶频率，计算结果与有限元模型对比，如表4所示。两点约束下频率的计算值最大误差不足2%，满足工程计算需求。

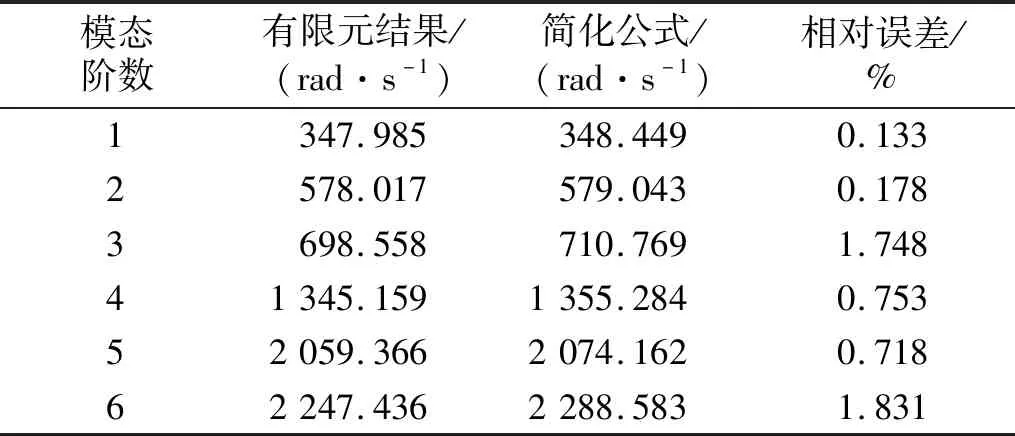
表4 前6阶频率对比Tab.4 Comparison of the first six frequencies

当结构的频率为0(即λ=0)时，式(28)所求的N=-8.508×103kN即为钢梁的欧拉临界力。此外，本文方法可服务于优化布设结构的约束位置和数量。当约束个数确定时，为了使压杆有最佳的稳定性，可根据欧拉临界力公式求出以c1,c2,c3，…为自变量下的最值N，保证压杆拥有最大的欧拉临界力(以钢梁为例，两点约束位于跨距比l1∶l2∶l3=1∶1∶1处时，为最大欧拉临界力Nmax=-9.158×103kN)；当欧拉临界力确定时，可根据不同约束个数下欧拉临界力公式的最值N，选出所需的最少附加约束，保证最佳的经济效益。

2.3 固支梁在单点约束下的频率

以两端固支且轴向受压的混凝土柱为例，混凝土柱长度8 m，圆形截面采用直径0.2 m，附加约束位于跨距比l1∶l2=3∶5处。有限元模型同样采用一维梁单元且等间距划分单元，梁端边界采用固结 ，中间支承仅约束竖向位移，具体参数如图5、表5所示。

图5 混凝土柱结构示意图Fig.5 Schematic diagram of concrete column structure

表5 混凝土柱模型的材料参数Tab.5 Material parameters of concrete column model

将混凝土柱尺寸及材料参数代入式(34)，对该方程组进行求解可得混凝土柱的基频，并将计算结果与有限元模型对比。如表6所示，固支梁在单点约束下基频的计算值误差仅1.39%。

表6 基频对比Tab.6 Fundamental frequency comparison

3 结 论

本文采用特征函数集和相应的特征值建立基本结构的势能泛函方程，利用拉格朗日乘子法考虑泛函中的附加约束条件，推导了轴向力作用下多点约束杆件横向振动的频率方程，同时获得了振动频率及欧拉临界力的解析解。主要结论如下：

(1)该方法同时获得了振动频率和欧拉临界力，理论上解释了欧拉临界力和振动频率的关系。

(2)杆件随着轴向压力的增大，固有频率逐渐减小；当频率降低至零时，结构发生失稳，因此对本方法所求的频率公式中λ=0时，即可得到杆件在多点约束下的临界欧拉力。

(3)简化了多点约束杆件固有振动频率的问题，该方法不受中间约束数量影响，可通过少量特征函数项求解结构频率，且特征函数项数越高，计算的频率精度越高。

(4)由式(24)、式(28)可知，欧拉临界力的大小不仅与梁长、端部支承方式、弹性模量和惯性矩有关，还与中间支承的个数和位置有关，因此合理布置附加支承可提高构件的稳定性。

(5)结构设计中可根据本方法所求的欧拉临界力公式反算得到构件需要附加支承的个数及位置的最优解。

(6)利用本文方法仅保留少数项特征函数即可求得低阶振动频率及相应临界欧拉荷载，适合快速手算。

通过实例分析可知，对于两端简支和两端固支的均匀连续梁，本文的计算结果与有限元分析的计算结果基本一致，该方法也适用于其他端点约束情况。