基于正态随机向量理论建构下的Fisher定理的证明

安佰玲，陈书凤，夏亚玲，王国华

（淮北师范大学 数学科学学院，安徽 淮北 235000）

0 引言

正态随机向量理论是正态总体统计推断基础，它包括正态随机向量及其函数的分布和独立性等问题，不少学者围绕该问题开展理论研究及其应用综述［1-7］. 笔者认为在数理统计课程学习之前，需要对正态随机向量的一般理论进行梳理和建构，这不仅是对概率论中低维随机变量理论内容的回顾和延伸，更重要它也是统计学专业的基础课程和后续专业核心课程的理论基础，同时Fisher定理也是该理论体系中的一个自然的结果. Fisher定理，描述的是单正态总体下样本均值和样本方差的抽样分布及其关系，三大抽样分布也是基于该定理构造的. 关于Fisher定理的证明，国内的大部分教材［8-11］，通过构造正交矩阵利用正交变换法证明，但是这种方法不够直观. 针对非数学专业学生，文献［12］和文献［13］避开矩阵代数的相关理论，利用正态随机样本的性质、变量变换定理和数学归纳法对Fisher 定理进行证明. 矩阵代数的相关理论是数学各专业的专业基础知识，同时也是统计学专业进一步学习多元统计及回归分析等核心课程的基础. 因此笔者认为，结合矩阵代数的相关理论，对正态随机向量一般理论进行梳理和建构，不仅能够实现对矩阵代数理论理解和应用、概率论内容的深化与完善以及Fisher定理的证明，同时为后继课程的学习奠定基础.

1 n 维随机向量及其分布

设X=(X1,X2,…,Xn)T，Y=(Y1,Y2,…,Ym)T分别为n维和m维连续型随机向量，其概率密度函数分别为f1(x1,x1,…,xn)与f2(y1,y1,…,ym).

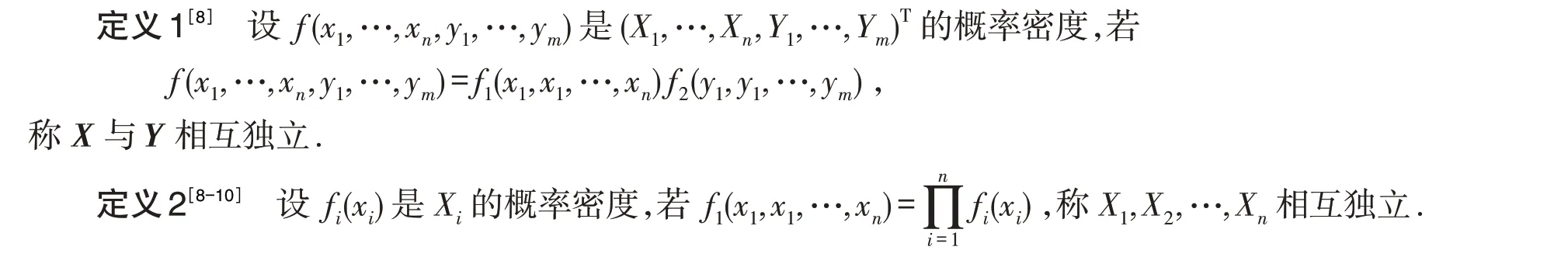
2 n 维正态随机向量的一般理论

2.1 正态随机向量的定义

定义4［14］若n维随机向量X=(X1,X2,…,Xn)T的概率密度函数为

2.2 正态随机向量的性质

定理1 设X1,X2,…,Xn独立同分布，且Xi～N1(μ,σ2)，则X～Nn(μ1,σ2In).

定理1由定义2及定义4可证.

是Σ的特征根，Q为n阶正交阵. 推论2 表明标准正态随机向量经过正交变换后仍为标准正态随机向量.

推论3 设X～Nn（μ,Σ），则ΕX=μ,Cov(X)=Σ.

推论3由引理3、推论1及定义3、4可证得.

推论3表明n维正态随机向量的分布完全由X的均值向量和协方差矩阵Σ确定. 协方差矩阵Σ描述n维正态随机向量各分量的波动程度及分量之间的关系，并且各分量之间的相互独立和两两不相关是等价的. 同时n维正态分布具有“再生性”，即n维正态随机向量任意维数的子向量仍服从正态分布. 具体描述为下面的定理.

定理3中（1）的证明由定义1及定义4可得，（2）可由（1）和定理2以及矩阵分块运算理论证明.

由定理2可知，正态随机向量经过可逆线性变换后仍然服从正态分布，其实这个结论可以推广到行满秩线性变换，即有如下定理.

定理4［1-2,14-15］设X～Nn（μ,Σ）,A为m×n矩阵，R(A)=m,b为m×1 非随机向量,则AX+b～Nm（Aμ+b,AΣAT）.

定理4的证明可以利用A构造一个满秩方阵，结合定理2和定理3证得.

推论4 设X～Nn（μ,Σ），c为n维非零向量，则cTX～N1（cTμ,cTΣc）.

推论4 由定理4 可证. 结合定理1，推论4 表明多个独立正态随机变量的线性组合仍为正态随机变量.

2.3 正态随机向量二次型的分布

本节主要讨论X的二次型的分布，即形如f(X)=XTSX的分布，其中S为n阶对称阵.

2.4 正态随机向量函数的独立性

对于n维正态随机向量X，由定理3可以通过其协方差矩阵来判断子向量间的独立性. 本节主要给出X的线性函数之间的独立性判定定理.

3 Fisher定理的证明

3.1 Fisher定理的证明

3.2 Fisher定理证明的概念图

基于正态随机向量的基本理论建构下的Fisher定理的证明及设计思路，利用概念图表示如下：

图1 基于正态随机向量理论的Fisher定理证明的概念图