基于特征加权融合的NOMA系统频谱感知方法

吴静怡，徐天衡，周 婷，胡宏林

(1.中国科学院上海高等研究院，上海 201210；2.中国科学院大学 ， 北京 100049；3.上海前瞻创新研究院，上海 201100)

0 引言

信号感知和动态频谱利用是世界各国围绕下一代通信系统的热点[1-3]。在这样的发展需求下，频谱感知(Spectrum Sensing,SS)技术的提出在一定程度上有效地缓解了频谱资源紧张的问题[4]。同时，考虑到未来更为复杂的通信环境和需求，下一代通信系统中会涉及大量的非正交多址(Non-orthogonal Multiple Access,NOMA)场景[5-6]。NOMA技术的主要特点是将信号以非正交形式在同一频谱上传输，以达到提高频谱利用率、增加系统容量等目的[7-8]。

如何将新型SS技术与复杂的下一代通信系统相契合是一个亟待解决的问题[9-11]。近几年来，有不少学者研究了在NOMA场景下SS的设计和应用，例如将次用户作为信号中继[12]或者应用于感知物联网(Internet of Things,IoT)[13]等，来提高频谱利用率、能量效率或吞吐量[14]。文献[15]对两用户下行NOMA场景提出了基于特征的SS技术并设计了一系列的工作流程，验证了该方法检测性能的稳定性。

考虑到下行NOMA频谱感知的特点，本文在前述基础上提出了一种基于多用户NOMA频谱感知的基于权重的融合合并判决方法，该方法是考虑到NOMA下行的特点而设计的；设计了系统模型和工作流程并推导得出所提方法对应的阈值表达式，并基于各种方法的特点设计了改进的联合判决算法，以进一步优化性能和效率；仿真验证了所提加权融合方法的可行性，证实了所提方法的性能优于现有的技术。

1 系统模型和基本感知原理

1.1 系统模型

不失一般性，本文考虑下行场景下2个基站(Base Station,BS)和N个用户的模型，如图1所示。主用户(Primary User,PU)为BS1，发送N个用户的信号，次用户(Secondary User,SU)为BS2，接收到这个信号并对信号的状态进行判断。若PU没有占用目标频段的结论，则SU占用该频段给这些用户发送信息;反之,则SU不进行传输。

图1 下行多用户模型Fig.1 Multi-user model of downlink

本文设定BS将N个用户信息同时以NOMA形式结合并向用户发送。N个信号的状态相同，即同时传输或不传输。下行NOMA概念如图 2所示。

图2 下行NOMA概念Fig.2 Concept diagrams of downlink NOMA

值得注意的是，由于特征检测技术能同时感知到多个信号的特征，因此更为适合在多用户场景下使用。本文使用特征检测方法，采用循环延时分级(Cyclic Delay Diversity，CDD)技术和双天线来得到各个用户信号的特征[16]。系统参数如下。

r(n)=ht(n)+w(n)，

(1)

式中，h=[h1,h2]；t(n)=[t1(n),t2(n)]T；w(n)为高斯白噪声(AWGN)。h1和h2是BS的2根天线和接收端之间的信道参数，t1和t2分别为2根天线发送出的信号，可以表示为：

(2)

(3)

式中，δi为用户i的循环位移，设定各个用户的位移值各不相同。

在接收端通过下式来得到信号的特征值：

(4)

式中，S为接收信号的长度；符号(·)*为共轭运算。当δ取到用户的循环位移值时，会得到一个峰值，称之为该用户的特征值。

1.2 SS判决原理

在感知判决中，将得到的用户i的峰值|Fi|与设定的阈值相比较。这是一个二元假设检验问题，假设H1为主用户信号存在的情况，H0为主用户不在传输的状态。接收信号的2种状态如下：

(5)

那么，判决过程可以表示为：

(6)

在此基础上，检测概率(Detection Probability)Pd表示的是SU正确感知PU在传输状态的概率，可以表示为：

(7)

虚警概率(False-alarm Probability)Pf是在PU实际未占用目标频段资源时，SU错误判断其状态的概率，可以表示为：

(8)

这2个参数相互关联，同时变化。研究者们研究SS方法的目的是在保证SU在较高概率利用空闲频谱的情况下，减小对PU信号的影响。

2 融合合并判决方法

2.1 方法设计

如图2所示，考虑到系统模型的特点为N个用户的传输状态相同，为了提高该系统检测概率，本文使用了k-out-of-N融合规则[17]作为现有方法并将之融合进本文的下行NOMA频谱感知模型中，同时提出了加权融合合并规则作为本模型中SS的判决方法[18]。

k-out-of-N方法是一种硬合并，指的是在N个对象中，若有不少于k个为“1”，那么结果也为“1”。当k=1时，即为OR规则；当k=「N/2⎤时，即为多数(Majority)规则；当k=N时，即为AND规则。

(9)

以一个3用户下行NOMA感知模型为例，图3和图4展示了用户的特征幅值以及各个方法得出的阈值。从图中可以明显看出3个用户的特征幅值和各个阈值的关系。

图3 3个NOMA用户的特征幅值以及3种硬合并的阈值Fig.3 Feature amplitudes of NOMA signal of three users and the thresholds of three hard combination rules

图4 3个NOMA用户的特征幅值以及加权算法的阈值Fig.4 Feature amplitudes of NOMA signal of three users and the thresholds of weighted rules

2.2 虚警概率-阈值推导

由于Pd和Pf两个参数相互关联，将Pf固定，用Pd的大小来表示检测性能的优劣。因此，需要通过固定的Pf来反推出阈值λ的表达式。

(10)

接下来分别计算各种规则的虚警概率与阈值的关系式。

k-out-of-N方法涉及到一个排列组合的问题，不失一般性，在N个用户的系统中，Pf可以统一表示为：

(11)

考虑到NOMA系统中如果由较多的用户共享同一个频段，会对各个用户的性能都造成一定的影响，且该式子由项数的多次方组成，解析过程较为复杂，故在此选择一个3用户模型，即N=3。因此，在k=1,2,3时分别为OR，Majority以及AND规则。下面对3种方法的虚警-阈值表达式分别进行推导。

当k=1时，Pf可表示为：

(12)

由此可以解出OR规则下的阈值为：

(13)

当k=2时，Pf可表示为：

(14)

(15)

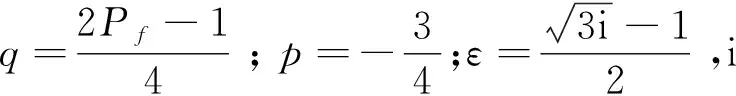
由此可以解出Majority规则下的阈值为：

(16)

当k=3时，Pf可表示为：

(17)

由此可以解出AND规则下的阈值为：

(18)

下面计算加权融合合并规则的阈值。该方法的Pf可表示为：

(19)

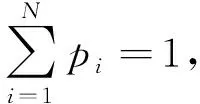
(20)

运用以上推导得出的公式进行仿真得到各个规则的检测性能，并进行对比。

2.3 改进的联合判决方法

经过性能的预实验之后，了解到不同方法的性能情况，考虑到各个判决方法之间性能的优劣以及趋势曲线有交叉的情况，本文提出了改进的联合判决算法，在已知用户功率比的情况下选择最适合的判决方法。

已知各信噪比下各个用户功率比的性能变化趋势，并能通过查询得到各个方法在当下信噪比以及功率比时的检测概率。所提的加权方法在性能上有一定的优势，但由于需要分别计算3个用户的特征值并对其进行加权融合合并判决，相对只要检测一个用户信号状态的U1方法，在时间成本上有明显的劣势。考虑检测性能和时间成本，提出的算法1在加权方法和仅检测最大功率用户U1的方法中选一个高性能高效的判决方法。假设一个较小的性能差距的阈值为Pd,Δ，当2个方法检测概率的差值绝对值小于该阈值，则表明2个用户性能接近，因此选择时间效率较高的U1方法。该算法流程简单且灵活方便，具体如下所示。

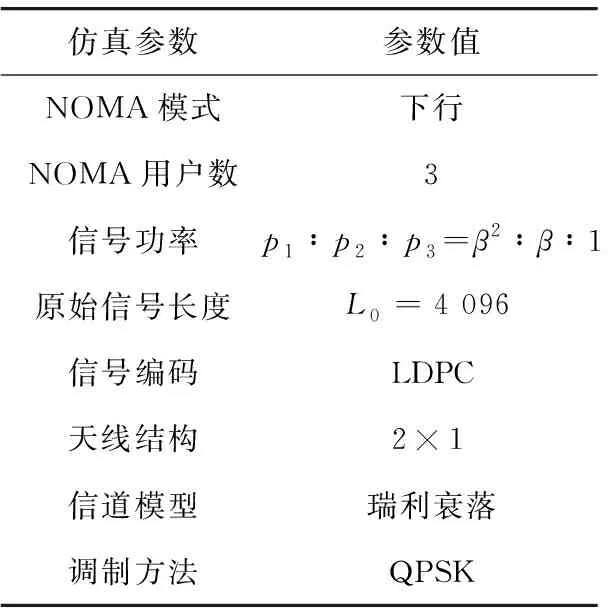
算法1 改进的联合判决算法输入:场景信噪比SNR;用户功率比β;各种方法关于检测概率和SNR、功率比的经验表;系统初始化;if(SNR或β产生变化) then获取SNR和β;根据SNR和β,获取经验表中2个方法对应的检测概率理想值Pd,w和Pd,U1;if(Pd,w-Pd,U1

3 仿真结果及分析

通过数值仿真验证表达式的准确性以及所提方案的可行性。按照前述流程得到各个用户的特征值，与阈值相比较，并根据规则得出判决结果，最后以蒙特卡罗方法得到相应的Pd和Pf。本文固定统一的Pf=0.1，以Pd的高低来表现检测性能的优劣。选取该系统下功率最大的用户U1的在相同条件下的检测概率作为基准，在环境SNR和功率参数β两个维度下比较4种规则的检测性能。

仿真的相关参数如表1所示。为了便于比较，本文设定3个用户的功率为等差。

表1 仿真参数Tab.1 Simulation parameters

本文选择β=1.2,2,3，即用户功率比分别为p1∶p2∶p3=1.44∶1.2∶1,4∶2∶1,9∶3∶1为例来展示不同功率比下的性能。图 5给出了β=1.2时5种判决规则下的Pd和Pf曲线趋势。可以明显看出，所有规则的Pf都严格保持在0.1。在低SNR时所有规则的Pd都保持一个较低的水平;在高SNR下的检测效果较高，当SNR为5 dB时Pd都近似达到了1。在4种判决规则中，加权规则以及OR，Majority规则的检测性能都优于只检测功率最大用户U1，其中加权规则为优，在-4 dB左右达到了0.9的检测概率。AND规则略逊于参考值U1。加权和AND这2个规则的Pd曲线之间最多相差了0.165。

图5 β=1.2时的3用户NOMA系统感知概率Fig.5 Sensing probability of three-user NOMA system when β=1.2

图6和图7分别展示了β=2,3时5种判决规则下的概率曲线趋势。

图6 β=2时的3用户NOMA系统感知概率Fig.6 Sensing probability of three-user NOMA system when β=2

图7 β=3时的3用户NOMA系统感知概率Fig.7 Sensing probability of three-user NOMA system when β=3

可以看出，随着β的增大，用户之间的功率差距也越来越大。4种判决方法的性能相对用户U1都有一定程度的减弱，其中AND方法检测概率下降最为明显在β=1.2,2,3时分别在-2,0,2 dB左右达到Pd=0.9。OR，Majority规则从β=1.2时的优于U1方法，到β变大之后性能逐渐被U1方法所超过，并拉开了一定距离。值得注意的是，所提的加权方法始终优于其他4种方法，甚至在β=3即p1∶p2∶p3=9∶3∶1这种较为极端的功率比下都占有优势，检测概率略高于OR和U1方法。

接下来从用户功率这一维度来探寻性能规律。以参数β为自变量，考察不同用户功率比下的检测性能变化情况。图8分析的是在环境总SNR为-5 dB时，不同方法下检测概率随着用户功率比变化的趋势,Pf同样被固定在0.1。可以明显看出，随着用户功率比的增加和用户功率差距的拉大，加权方法、OR方法以及基准U1方法的检测概率随之增加并最后趋于一致，Majority，AND方法的检测概率明显呈下降趋势。这是由于某个用户的功率越小，检测该信号时越容易受到噪声的影响而产生错误判断。当β=1即3个用户功率相同这种边界情况时，各种方法由于对3个用户的判决结果进行了综合考虑，检测概率均大于U1方法。在4种判决方法中，检测性能以加权方法为最优，在图示的功率比β=[1,3]中，该方法始终优于其他的判决方法，检测概率能保持在0.85以上。同时,最高检测概率能高于基准U1方法0.131，高于仅次于该方法的OR方法0.038，这在SNR较好且整体性能水平较高的条件下相当占据优势。但毋庸置疑的是，仅考虑功率最高用户U1的方法的感知结果是时间成本最小的方法，以图示β=[2.4,3]部分为例，加权方法以极小的差距优于U1方法，但是分别计算3个用户的特征并融合判决所需的时间高于只感知一个用户的时间，在这种情况下，可以考虑用较小的性能劣势来换取较高的时间效率。

图8 -5 dB时的3用户NOMA系统感知概率Fig.8 Sensing probability of three-user NOMA system at -5 dB

图9展示了在环境总信噪比为-10 dB时，各个判决方法的检测概率随着用户功率比变化的趋势。-10 dB时感知性能的总体趋势与图8类似，但SNR降低拉大了性能曲线之间的差距。同时也突显出了所提加权方法性能的优越性，在低功率比下显著优于其他4种方法，在高功率比下逐渐和U1方法趋近。在图示的功率比中，加权方法的检测概率能保持在[0.5,0.6]，同时最高检测概率能高于基准U1方法0.172，高于仅次于该方法的OR方法0.078，体现了该方法在不同SNR下稳定的性能优势。

图9 -10 dB时的3用户NOMA系统感知概率Fig.9 Sensing probability of three-user NOMA system at -10 dB

4 结束语

本文基于多用户下行NOMA频谱感知场景，提出了一种加权融合合并判决方法,为所提技术设计了相应的工作流程，对该方法进行了虚警概率和阈值的闭式解推导，同时提出了一种适应不同SNR环境和用户功率比的判决方法选择算法。仿真结果表明，通过对多个用户的感知结果进行加权合并判决，所提技术在给定的各种情况下，检测性能都优于现有技术，进一步提升了SS技术在下一代无线通信中的优越性和竞争力。