基于改进蝙蝠算法的无人机三维路径规划

苏 菲

(湖北商贸学院 人工智能学院，湖北 武汉 430079)

0 引言

近几十年来，随着无人机技术的快速发展及成熟，使得无人机在军事行动中得到广泛应用[1]。在军事行动中，固定翼无人机常被用于情报收集、敌情侦察、物资补给，甚至武装攻击[2]。与有人驾驶飞机相比，无人机具有体积小、成本低、隐蔽性高和机动灵活等优势，可以精确地完成重复性任务，且不受机组人员疲劳管理限制[3]。此外，无人机可以通过远程控制，能在危及飞行安全的极端情况运行[4]。但目前无人机虽为无人驾驶，却并没有消除对飞行员的依赖，仍需要驾驶员远程控制，难以实现自主驾驶[5-6]。

要实现无人机的自主驾驶，首先需要实现无人机的智能路径规划。当前，关于无人机路径规划的研究主要集中于连接起点和终点的最佳轨迹计算，且无人机轨迹必须符合无人机的动态约束，须对目标函数进行最小化处理，以实现最小化燃料消耗和最小化平均高度[7]。在早期的研究中，主要使用简化的无人机模型及环境模型来表示，并依靠确定性算法计算最佳路径[8-9]。但早期研究均依赖于在大量迭代中改进候选解，最终收敛到准最优解，计算工作量较大，在飞行中执行路径规划耗时太长[10]。

因此，为实现无人机自主驾驶及飞行，众多专家学者针对无人机路径规划进行了大量研究。其中，文献[11]提出了一种基于改进人工势场的无人机动态避障路径规划方法，通过设置无人机与目标点的距离因子，调整斥力场系数，消除狭窄通道的轨迹振荡。文献[12]提出了一种基于改进A*算法的无人机路径规划方法，运用栅格法对无人机任务空间环境进行建模，提高了节点的搜索效率。但上述方法均属于经典路径规划方法，算法运算时间较长，且容易陷入局部最优，实际应用效果不佳。文献[13]提出了一种粒子群优化算法，通过考虑地形掩蔽、非各向同性雷达散射截面及无人机的动态约束等因素来确定路径规划。文献[14]提出了一种混合灰狼路径规划优化算法，通过简化计算阶段加快收敛速度并保留种群探索能力，从而获得有效的最佳飞行路径。文献[15]提出了一种基于蚁群优化算法的航迹规划方法，在启发函数中加入路径偏移因子，降低了航迹搜索空间的复杂度。但上述方法均属于元启发法，需要强大的计算能力，导致消耗大量的计算时间，不利于无人机执行快速反应、机动灵活的作战任务。

为此，针对上述研究问题，提出了一种融合黄金正弦和蝙蝠算法(Golden-Sine Bat Algorithm，GSBA)的无人机三维路径规划方法。首先，通过在传统蝙蝠算法(Bat Algorithm,BA)中引入黄金正弦算法，提高蝙蝠个体寻优能力；采用平均种群位置对剩余个体进行引导，提高种群的多样性。其次，引入删除操作降低路径的冗余度。最后，通过搭建仿真环境，验证了所提方法的有效性。

1 模型构建

为了便于模型构建，假设突然发生泥石流或者其他的灾害造成通往山区的公路无法通车，为了解决山区内居民生活物资问题，采用无人机进行物资的运送。假设山区空间大小为a1km×b1km×c1km，其中无人机运输途中的障碍物主要为山体，即：

(1)

式中，Zi(x,y)为单个山体函数，即山体i上的某点(x,y)的高度；k1为表征山体形状的系数；k2为表征山体大小的系数。山体i的中心点坐标为(xi,yi)，xpi，ypi分别对应山体i的x轴和y轴2个方向上的坡度。

无人机安全运输的要求是能够避开飞行途中的所有障碍物(即山体)，这也意味着在坐标点(xm,ym)处无人机的飞行高度要高于障碍物的高度，否则无人机将与山体相撞，即：

V(xm,ym)>Zi(xm,ym),xm∈Si,ym∈Si，

(2)

式中，V(xm,ym)为无人机在点(xm,ym)的飞行高度；Si为山体i在xy平面上的投影区域。

通常无人机具有一定的体积，如果单纯使用无人机中心点计算无人机高度，可能会出现无人机边缘撞击山体的事故，所以还要考虑无人机机体与山体的距离是否会发生碰撞。因此，将UAV模型简化为一个长方体，其长宽高分别用符号a，b，h表示，简化后无人机与山体的位置关系如图1所示。

图1 长方体无人机与山体的位置关系Fig.1 Position relationship between the cuboid drone and the mountain

由图1可知，如果根据式(1)和式(2)计算，在坐标(xm,ym)处，虽然无人机的飞行高度比该点山体要高，但是由于山体自身存在坡度，无人机在飞行过程中势必还是会与山体相撞。这也意味着无人机与山体之间的避撞不仅与无人机体积有关，同时还与山体的陡峭程度有关，但是山体表面往往是非线性变化区域，因此对山体建模存在一定的困难。为了解决上述问题并避免无人机与山体发生碰撞，将无人机进一步简化为球体，球体的直径为无人机机体对角线最长部分，如图2所示。

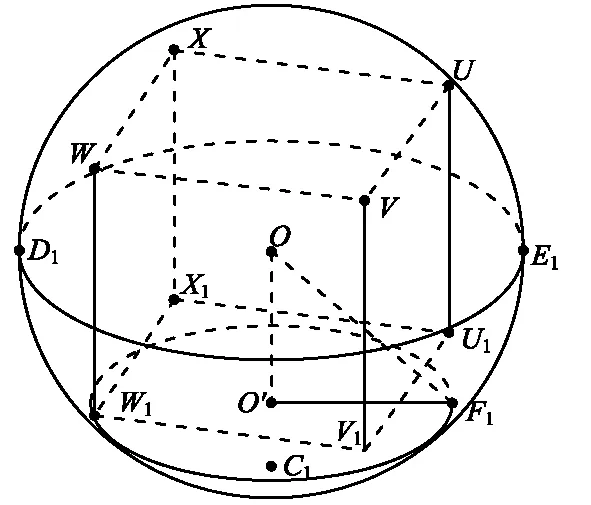
图2 无人机球体模型Fig.2 UAV sphere model

其中，图2也可以理解为将图1中无人机简化的长方体放置在一个球体中，球体半径为：

(3)

为了对球体更好地进行描述，此处使用极坐标表示，该坐标系原点为无人机中心，即：

(4)

式中，R(x,y,z)表示球体R上的一个点，将R(x,y,z)与极点连成一条直线L，则θ表示z轴的正方向与L的夹角；将R(x,y,z)与z轴形成一个平面M，则φ为坐标系中z轴和x轴所形成的平面与平面M之间的夹角。

由此可以得到，如果球体R上的任意点(x,y,z)均在山体外部，则不会发生无人机碰撞山体事件，即：

R(xm,ym,z)>Zi(xm,ym),xm,ym∈Si。

(5)

此外，还要考虑无人机飞行高度超过限值导致的脱离无线控制信号范围的问题，以及无人机飞行高度过低导致的可能与地面物体(如地表植物、石头等)发生碰撞的问题，所以无人机飞行高度还应满足：

Hmin≤Hi≤Hmax，

(6)

式中，Hmin为无人机飞行高度最小值；Hmax为无人机飞行高度最大值。

为了对无人机飞行的路径质量进行评价，还需要构建以飞行路径高度、长短和平滑度等为目标的评价指标。无人机飞行路径中点i与点i+1之间的距离为：

(7)

式中，(xi,yi,zi)表示无人机飞行路径点i在xzy三维坐标系中的坐标，此时无人机的飞行路径总长度为：

(8)

式中，N表示无人机飞行过程中途经的点的总数。无人机飞行路径中的转角角度如图3所示。

图3 无人机飞行转角Fig.3 UAV flight angle

从图3可以看出，θ为无人机从路段AB转至路段BC所需要转的角度，故可以计算无人机飞行路径的平均平滑度为:

(9)

式中，Ai为无人机飞行路径中的点i与点i+1连接而成的向量。同时，因为无人机飞行高度越高能耗也越高，故无人机在安全飞行的前提下须尽量低空飞行。无人机从起点到终点飞行高度平均值为：

(10)

综合式(7)～式(9)中的无人机路径规划目标，可得目标函数为：

minM=Lall+Q+Hall。

(11)

2 改进BA

2.1 传统BA

BA是指根据蝙蝠的飞行行为而得到的一种启发式算法[16]。首先，构建适应度函数并计算种群中个体的适应度值；其次，比较个体适应度值，并记录其中适应度值最高的蝙蝠个体作为全局最优蝙蝠，同时根据此最优蝙蝠个体的信息对其他蝙蝠个体的位置和速度进行更新。然后对最优个体通过一定的局部搜索方法进行局部搜索，并更新其位置信息，不断迭代此过程直到得到全局最优解。传统BA更新过程为：

fi=fmin+(fmax-fmin)β，

(12)

(13)

(14)

全局搜索完成后可以得到全局最优蝙蝠个体，而后需要进一步通过局部搜索方法对该蝙蝠个体的周围进行搜索，即在最优蝙蝠的周围进行随机游走，此时使用式(15)进行位置更新。

xnew=xold+εAt，

(15)

式中，xold为当前最优蝙蝠个体的位置；xnew为局部搜索更新后的最优蝙蝠个体位置；ε∈[-1,1]；At表示t次迭代中的种群平均响度。

当蝙蝠飞行过程中发现了猎物，为了更加准确地对猎物的位置进行定位，蝙蝠个体的声波脉冲频率会增加，响度会减小，位置更新为：

(16)

(17)

2.2 融合黄金正弦的BA

2.2.1 黄金正弦算法

黄金正弦算法(Golden-SA)为一种新型智能算法[17]，通过单位圆和sin函数的关系在算法迭代寻优的过程中进行全局搜索，同时使用黄金分割数对空间进行控制遍历，实现个体的快速寻优，该算法计算简单且迭代收敛快。

其位置更新为[18]：

(18)

a1=-π+(1-τ)2π，

(19)

a2=-π+2πτ，

(20)

2.2.2 种群平均位置

由于BA中的寻优是根据其中最优蝙蝠个体的引导而进行的，所以若全局最优蝙蝠个体并非种群最优个体且相差较大，则会导致算法陷入局部最优。针对此问题，为了避免蝙蝠个体引导方向错误，对于种群中蝙蝠个体的引导搜索还可以加入种群平均位置引导，进而极大可能地避免了局部最优问题。具体更新为：

(21)

(22)

式中，mt-1表示引入的t-1次迭代中的种群平均位置。

2.2.3 分阶段局部搜索

在传统的BA中通常是采用全维搜索方法，该方法虽然具有较强的局部搜索能力，却忽略了单个维度值对算法适应度的影响。但是若采用单维度搜索算法，又会导致算法收敛速度慢，影响搜索效率。

考虑到上述因素，本文将全维搜索与单维搜索相结合形成互补的搜索方式，实现对最优蝙蝠个体的搜索。融合后的搜索方式为在每次迭代的前2/3过程中使用单维搜索，后1/3使用全维搜索，具体更新为：

(23)

式中，T表示最大迭代次数；d∈[1,D]。

2.2.4 删除操作

由于路径规划中会存在冗余节点的问题，为了提高路径平滑度、降低路径长度，还需要删除冗余节点，如图4所示。

图4 删除操作示意Fig.4 Schematic diagram of delete operation

由图4可知，在删除操作之前算法规划的路径为1→2→3，将节点1和节点3相连接，如果可以避开障碍物，则1→3路径可行且安全，那么可以对节点2进行删除操作。

从第一个节点开始，依次连接后面的节点，如果连接的直线为无障碍路径，则将2个节点中间的节点都删除；如果不存在无障碍路径，则从下个节点开始继续搜索，直到最后一个节点。而后，重新对路径适应度进行计算。通过删除操作，一方面通过减少冗余节点缩短了路径的长度，另一方面也提高了路径的平滑度。

2.2.5 引入黄金正弦的BA

为了避免算法早熟，提出了一种改进BA，即引入黄金正弦思想。首先，将蝙蝠种群分成2个具有不同适应度的子种群，对于其中适应度较好的子种群，使用sin函数更新个体位置，进而使最优个体信息可以迅速引导影响其他个体，实现了算法的快速收敛，对于另外一个适应度较差的蝙蝠子群体，则通过种群平均位置避免了其他个体搜索方向的偏移，保证了算法多样性，避免局部最优。此时，蝙蝠个体位置更新为：

(24)

算法全局搜索后，还要进行局部搜索，即通过全维搜索策略和单维搜索策略相结合分阶段互补搜索，提高了算法的局部搜索能力。获得最优解后，再通过删除操作对其中的冗余节点进行删除，最终得到了平滑度高、路径长度短的最优路径。

本文算法的流程如图5所示，具体步骤如下：

图5 本文所提算法的流程Fig.5 Flow chart of the algorithm proposed

② 对蝙蝠种群中每个蝙蝠个体的适应度进行计算，对其中最优的路径x*进行记录并保存，而后根据式(22)对蝙蝠种群的平均位置进行计算。

③ 根据式(24)更新最优蝙蝠个体位置，而后使用式(21)和式(14)对其他蝙蝠个体进行更新。

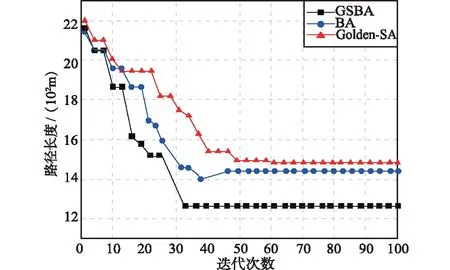
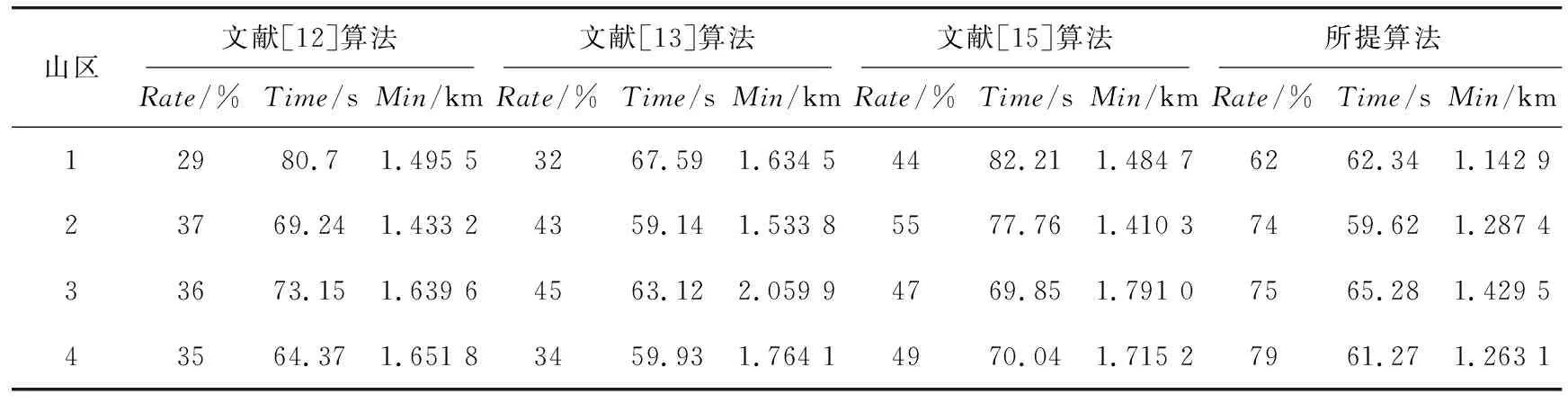
每次迭代中更新全局最优路径，而后计算其适应度值。若t=T，那么删除最优路径中的冗余节点，输出结果。若t

3 实验结果分析

实验中假设无人机需要向4个1 000 m×1 000 m×1 000 m的不同山区运送物资。将1 000 m×1 000 m×1 000 m的山区空间离散为109个坐标点，UAV的参数(a,b,c)=(0.5,0.6,0.5)m,Hmax为1 000 m,Hmin为10 m，算法中种群个体N为100，最大迭代次数T为100，脉冲频率fmin=0.0,fmax=2.0，初始脉冲发射率r0=0.5，脉冲和响度调节参数为0.9。

山区1的起点坐标为(1,5,0)、终点坐标为(10,5,0)。山区2的起点坐标为(0,5,0)、终点坐标为(10,5,0)。山区3的起点坐标为(2,9,0)、终点坐标为(10,0.5,0)。山区4的起点坐标为(0.5,3.5,0)、终点坐标为(9.5,9.5,0)。为了验证改进后的算法的性能，首先选取山区1进行算法迭代验证，实验中分别选取了传统BA、Golden-SA以及本文所提改进算法对山区1优化路径进行求解， 3种算法的飞行路径如图6所示。

图6 3种算法对山区1规划的无人机飞行路径Fig.6 UAV flight path planned by the three algorithms for mountain area 1

由图6可知，3种算法规划的飞行路径区别较大，山区1中3种算法的迭代图如图7所示。

由图6和图7可以看到，BA规划的路径长度和达到收敛的迭代次数与Golden-SA都较为接近，而改进后的算法在经过32次迭代后就得到最优飞行路径，且路径长度要明显低于其他2种算法，由此也表明在融合了传统BA和Golden-SA后，所得到的算法在性能上有了很大的提高。

图7 山区1中3种算法迭代Fig.7 Three algorithm iterations in mountain area 1

为了验证本文所提改进BA的有效性，选取了文献[12]、文献[13]和文献[15]三种算法进行对比分析，分别对山区1～4进行无人机路径规划。4种算法的规划路径图如图8所示。

(a) 山区1

(b) 山区2

(c) 山区3

(d) 山区4图8 山区1～4环境中4种对比算法规划的路径Fig.8 Paths planned by the four comparison algorithms in mountain 1～4 environments

从图8可以看出，在山区1～4环境中本文所提算法的路径要明显比其他3种算法的短，且路径更为平滑。4种算法在山区1环境下的算法迭代情况如图9所示。从图9中可以看出，所提算法在经过35次迭代后就获得了最优路径，其迭代速度明显比其他3种算法快。为了更直观地体现所提算法的性能，表1给出了4种算法的具体仿真参数，其中Min表示飞行路径长度、Time表示算法迭代时间、Rate表示种群中个体的收敛率。

图9 不同种算法在山区1路径规划中的迭代Fig.9 Iteration of different algorithms in mountain area 1 path planning

表1 不同算法路径规划指标比较Tab.1 Comparison of path planning indicators of different algorithms

4 结束语

针对当前无人机在高速动态环境中轨迹调整自主性低、响应速度慢的问题，提出了一种基于改进BA的无人机三维路径规划方法。实验结果表明，本文所提算法在路径长度、算法收敛时间以及种群收敛度方面有着良好的性能，能够有效实现无人机的三维路径规划。但是需要注意的是，本文在路径规划方面的优势需要建立在对飞行环境的精准建模基础上，若建模出现误差则可能会导致无人机坠毁，而对于复杂山体的建模仍然较为复杂，因此后续也将重点研究如何通过复杂山体模型构建来避免无人机与山体碰撞。