拉普拉斯变换在精确求解二体阻尼震荡模型中的应用

刘嘉贤，王文佳，麻嘉欣，李喜彬

(内蒙古师范大学 物理与电子信息学院，内蒙古 呼和浩特 010022)

拉普拉斯变换在解带有初始条件的线性常微分方程时可以发挥巨大的作用.但在数学物理方法的教学过程中，常常省去这部分内容，因为相较傅里叶变换，拉普拉斯变换确实存在着相应的局限性.但在处理某些问题时，应用拉普拉斯变换可以给出精确的解析解，比如线性非齐次常微分方程的通解问题等.因此在教学过程中花费较少部分的学时来简单扼要地介绍拉普拉斯变换，对于学生深入理解高等数学中相关内容是大有帮助的.

二体系统作为多体系统中的可解模型之一，它在经典力学中起着极其重要的作用.多体系统随着研究对象数量的增加，其动力学演化轨迹变得不可预测，而且不确定性显著增加，系统更加难以研究[1]，同时多体系统常常伴随着混沌现象.因此，研究二体系统是处理复杂动力学系统的基础性工作.例如，在量子力学中，对相互作用的双原子系统的研究可以为多原子系统性质的分析提供有力的借鉴[2,3].在天体物理中，相互吸引的二体系统是唯一可解的模型，而在三个以上天体的系统中，其轨道具有很高的复杂性[4].多体线性系统也会随着不同的参数组合出现复杂的情况[5,6].

本文对一个简单的二体模型进行了解析计算，该模型包含两个由弹簧连接的物体，其阻尼力大小正比于物体的速度.通过对运动方程组进行拉普拉斯变换，将其转换为线性方程组，之后再利用拉普拉斯逆变换，就可以得到两个物体位置随时间的变化情况，即解析解. 在计算拉普拉斯逆变换的过程中，需要确定奇点的位置，用到了卡尔丹诺(Cardano)公式来求得一元三次函数的根.

1 微分方程组

在物理问题中经常出现由弹簧连接的两个物体，假设质量为m1和m2的两个物体分别由恢复系数为k的弹簧连接，其原长是a.将弹簧拉长至b，同时释放两个物体，变量x1和x2表示相对于释放处的位移，其模型如图1所示.假定阻尼力的大小与该物体速度成正比，阻尼系数为γ.上述系统的运动方程为

图1 运动方程式(2)对应的示意图.

(1)

或者重新写为更简单的形式：

(2)

(3)

(4)

(5)

(6)

f(s)=m1m2s3+γ(m1+m2)s2+

[γ2+k(m1+m2)]s+2γk=

ax3+bx2+cx+d

(7)

是有

f(z)=z3+pz+q

(8)

其中常数p和q分别为：

(9)

(10)

需要注意的是，多项式z3+pz+q最高次幂的系数已经调整为1(各项系数同时除以a)，这是因为我们只关心f(z)的零点.根据卡尔丹诺(Cardano) 公式[8]，方程(8)的根分别为：

(11)

(12)

(13)

与一元二次函数类似，在方程(13)中定义的Δ同样可以用来区分一元三次函数(8)所对应的根的不同情况：

1) 如果Δ=0，有3个实根且至少两个相等；

2) 如果Δ<0，有3个不同的实根；

3) 如果Δ>0，有一个实根和两个共轭虚根.

接下来对方程 (2) 的不同情况分别进行讨论.

2 临界阻尼振荡(Δ=0)

Δ=0的条件代表过阻尼振荡和欠阻尼振荡之间的状态，因此称之为临界阻尼振荡.这种情况所对应的判别式为

(14)

数值分析表明，式(2)作为阻尼系数γ的函数，只存在一个实的正根，或者说式(1)描述的动力系统只存在唯一的临界阻尼振荡状态.

而后我们可以用3种不同的情况来讨论这种状态.

2.1 q=0，p=0

这种情况需要3个等式，q=0、p=0以及Δ=0.然而，这3个方程不存在关于γ的正实根，所以这种情况不会在物理系统中发生.

2.2 q>0，p<0

这种情况下，多项式方程(8)的3个根分别为：

(15)

根据式(5)，物体m1的位移随时间的变化为

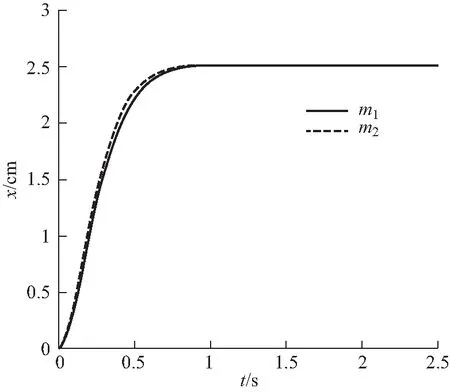
m1=0.5 kg，m2=0.4 kg,k=10 N·m-1,γ=6.036 kg·s-1图2 式(16)所对应的运动轨迹

(16)

上式中最后一项中的“撇”表示对变量s的导数.图2给出了物体m1和m2的轨迹.

2.3 p>0的情况

这里，我们对p>0的情况不做讨论.这是因为按式(13)中的定义，如果p>0，则Δ无法为零, 因此这种情况不会发生.

3 过阻尼振荡(Δ<0)

对于Δ<0的情况，一元三次方程(8)存在3个不同的实根，它对应着过阻尼振荡模式.与第2节的讨论方法相同，本节同样分为三种不同的情况进行讨论.

3.1 q=0,p<0

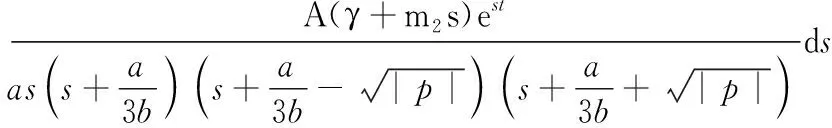
(17)

上式中，下标q=0表示约束条件.这种情况下的运动状态如图3所示.

m1=0.5 kg,m2=0.4 kg,k=10 N·m-1，γ=6.058 kg·s-1图3 式(17)对应的的运动轨迹.

3.2 q>0,p<0

这种情况下，3个零点之一的解析表达式为

(18)

式中，r为3次根号下的复数的模长，即

(18)

θ为复数的幅角：

(19)

另一个根表示为

r1/3(ei2π/3eiθ/3+ei4π/3e-iθ/3)=

(20)

最后一个根可以通过同样的方法获得：

(21)

而通过拉普拉斯逆变换得到的位移为

x1(t)=

(22)

以上的计算表明，变量a、b、r、θ、p和q与参数m1、m2、k和γ相关，因此式(23)的精确分析结果也是非常复杂的，为方便起见，本文在这里不做说明.式(23)的轨迹如图4中所示.

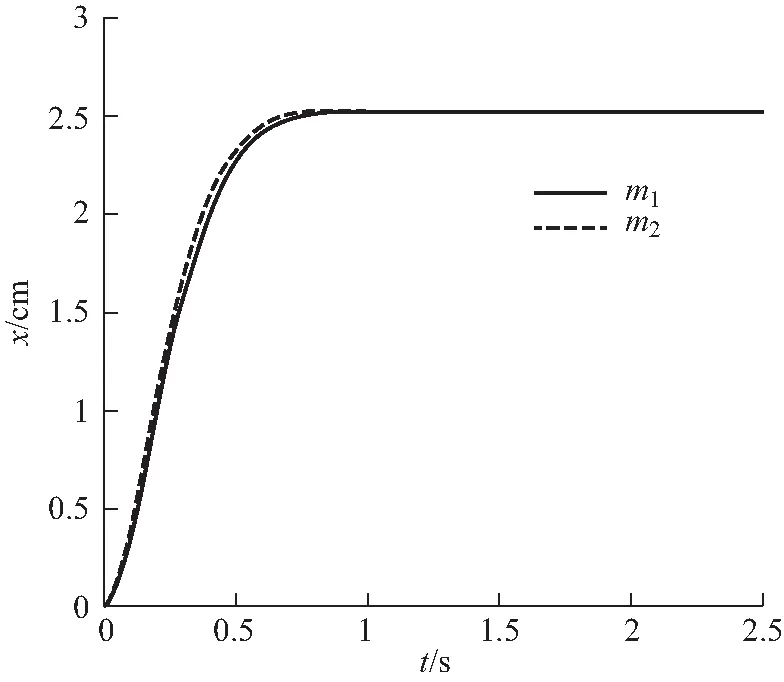
m1=0.5 kg，m2=0.4 kg，k=10 N·m-1,γ=5.058 kg·s-1图4 式(23)对应的的运动迹.

3.3 q<0,p<0

重复3.2节的计算过程，m1位移的表达式与式(23)的结果相同，其轨迹如图5所示.

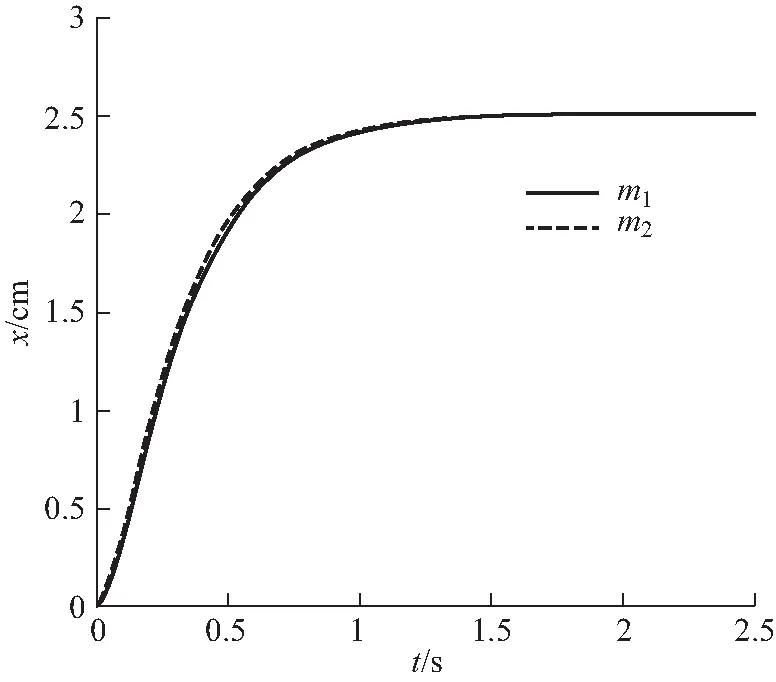
m1=0.5 kg,m2=0.4 kg，k=10 N·m-1,γ=7.058 kg·s-1图5 q<0和p<0的过阻尼振荡迹.

4 欠阻尼振荡

欠阻尼振荡对应于条件Δ>0，即一个实根和两个共轭虚根，在此情况下，两个物体的振幅振荡衰减.这种现象也类似于单体系统.

4.1 q=0,p>0

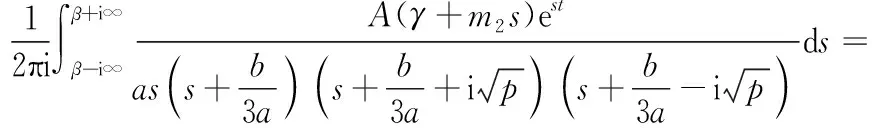
(23)

其中c.c.表示复数共轭.其演化图像如图6所示.

m1=0.5 kg,m2=0.12 kg，k=10 N·m-1,γ=0.964 kg·s-1图6 式(24)对应的的运动轨迹.

4.2 q>0

此时，式(8)的根为

(24)

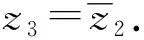
(25)

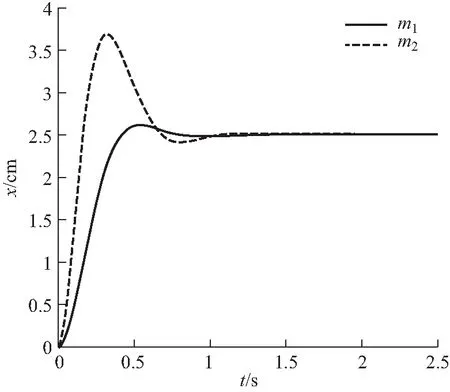
m2=0.12 kg,k=10 N·m-1，γ=1.663 8 kg·s-1图7 式(26) 对应的的运动轨迹.

m1=0.5 kg,m2=0.12 kg,k=10 N·m-1，γ=0.463 8 kg·s-1图

4.3 q<0

在这个条件下的解析结果与式(26)完全相同,其位移随时间的变化曲线如图8所示.

5 总结

本文计算了弹簧连接的二体系统在临界阻尼、过阻尼和欠阻尼三种情况下的振动模式.解析结果完全可以通过拉普拉斯变换、留数定理和卡尔达诺(Cardano)公式等方法得到，但是每种情况的公式都非常复杂.与单体振荡系统中的结果相类似，它仍然可以区分为三个条件，这三个条件 是由式(13)中定义的判别式Δ来区分的.每种模式的演化图像、相应的参数组合和说明如表1所示.与其他描述多体系统的模型相比,二体系统是一个相对简单的模型，但其结果却相当复杂.不难想象,精确求解多体系统几乎是不可能的.但是,这种方法仍然可以推广到多体系统的研究中.如式(4)所示,主导方程演化趋势的部分仅为分母的零点类型.因此,本文对多体动力系统的研究具有一定的参考价值.

表1 不同参数组合所对应的振荡模式

同时，从上面的计算中发现，在数学物理方法的教学实践中，适当地加入拉普拉斯变换对于开拓学生的视野、培养学生的学习热情都有一定的帮助.