State Estimation Moving Window Gradient Iterative Algorithm for Bilinear Systems Using the Continuous Mixed p-norm Technique

Wentao Liu,Junxia Ma and Weili Xiong

Key Laboratory of Advanced Process Control for Light Industry(Ministry of Education),School of Internet of Things Engineering,Jiangnan University,Wuxi,214122,China

ABSTRACT This paper studies the parameter estimation problems of the nonlinear systems described by the bilinear state space models in the presence of disturbances.A bilinear state observer is designed for deriving identification algorithms to estimate the state variables using the input-output data.Based on the bilinear state observer,a novel gradient iterative algorithm is derived for estimating the parameters of the bilinear systems by means of the continuous mixed p-norm cost function.The gain at each iterative step adapts to the data quality so that the algorithm has good robustness to the noise disturbance.Furthermore,to improve the performance of the proposed algorithm,a dynamic moving window is designed which can update the dynamical data by removing the oldest data and adding the newest measurement data.A numerical example of identification of bilinear systems is presented to validate the theoretical analysis.

KEYWORDS Bilinear state space model;parameter estimation;moving window;continuous mixed p-norm

1 Introduction

Although many physical dynamic behaviors are characterized as linear systems in the neighborhood of a single operating point,when they exhibit strong nonlinearities or must be described over the entire operating range,linear models may not yield appropriate results[1–3].Owing to that,the study of system identification and parameter estimation for nonlinear systems has drawn considerable attention of academic researchers [4–6].Various models are exploited to describe actual nonlinear systems with relatively simple structures [7–11] such as Hammerstein systems,Bilinear systems,and Wiener systems.

The parameter estimation of the system models is important for control system analysis and design.The parameters of the models can be estimated by using some identification methods[12–15]such as the hierarchical algorithms[16–19].In this paper,we confine our discussion to bilinear systems,which are simplicity in model structures and capable of approaching arbitrary nonlinear systems with much higher accuracy than traditional linear approximations theoretically[20].Bruni et al.designed a bilinear time-series model-based self-tuning controller for a multi-machine power system to enhance the region of stability of the system,and return the states to their stable equilibrium [21].Yeo et al.developed the bilinear model predictive control algorithm for paper plant systems to control the grade change operations in paper production[22].Wang et al.simulated the bridge nonlinear boundary as bilinear translational,and applied the nonlinear least squares optimization algorithm to identify the nonlinear translational and rotational boundary parameters of the bridge[23].

Many researches have been studied in the parameter estimation of bilinear state space systems.A stochastic gradient algorithm and a gradient-based iterative algorithm have been proposed for the parameter identification of bilinear systems by using the auxiliary model.The gradient-based iterative algorithm uses fixed batch data to update the parameters,so that the parameter estimation accuracy can be greatly improved compared with the stochastic gradient algorithm.Li et al.combined the maximum likelihood theory with the data filtering technique for bilinear systems with colored noises.The state observer is vital in the field of state estimation of bilinear systems [24].Tsai considered a H-infinity fuzzy observer for bilinear systems by means of a linear matrix inequality approach [25].Phan et al.presented a full-order bilinear state observer for the bilinear system,which optimized the observer gain by interaction matrices [26].Zhang et al.considered the state estimation problem of bilinear systems and proposed a state filtering method for the single-input single-output bilinear systems and multiple-input multiple-output bilinear systems by minimizing the covariance matrix of the state estimation errors [27].Recently,some state and parameter estimation methods have been proposed for linear and bilinear state space systems in the presence of exogenous noises[28–30].

However,in industrial applications,the dynamical processes often work on various noise environments,and some works used nonlinear filtering technique such as median filtering and least meanpnorm to overcome the problems.Zayyani proposed a mixed-norm adaptive filter algorithm for systems identification based on minimization of the logarithmic continuous mixedp-norm[31].Moreover,an improved mixedp-norm algorithm had been studied to combat non-Gaussian interference and its computational complexity as well as the mean convergence had also been analyzed[32,33].

Inspired by the above researches,we study the parameter estimation algorithms for bilinear state space models with the noise disturbances.Based on the iterative search and the state estimator,a bilinear state continues mixedp-norm gradient iteration(BSO-CMPN-GI)is proposed.The proposed algorithms control the proportions of the error norms and offer an extra degree of freedom within the adaptation.By taking into consideration eachp-norm of errors for 1 ≤p≤2,the proposed algorithms combine the benefits of the variable error norms and thus are more robust against noise interference.Furthermore,the moving data window theory is introduced to improve the effectiveness of the proposed algorithms.The contributions of this paper are summarized as follows:

· A state observer is designed to obtain the system states variables consisting of the product terms of state variables and control variables.

· A bilinear state observer-based continues mixedp-norm gradient iteration (BSO-CMPN-GI)algorithm is presented for the bilinear state space system under the noise interference to estimate the unknown system parameters.

· A bilinear state observer-based moving window CMPN-GI(BSO-MW-CMPN-GI)algorithm is derived to update collected data and thus maintain high data utilization.

The outlines of this paper are organized as follows.Section 2 introduces some definitions and proposes the identification model of the bilinear state space system and introduces a bilinear state observer for the state estimation.Sections 3 and 4 derive a BSO-CMPN-GI and a MW-CMPN-GI algorithms based on the bilinear state estimator,respectively.An example to illustrate the effectiveness of the proposed algorithms in Section 5.Finally,Section 6 gives some concluding remarks.

2 System Description and Identification Model

Consider the following single-input single-output bilinear state space modelblue:

whereut∈Rnis the system input variables,yt∈Rnis the measurement output variables,xtis the state vector,wtis an uncorrelated process noise with zero mean,andvtis an uncorrelated measurement noise with zero mean.A∈Rn×n,B∈Rn×n,g∈Rnandc∈R1×nare system parameter matrix and parameter vector.Consider the observer canonical form of bilinear systems,the system parameters can be expressed as

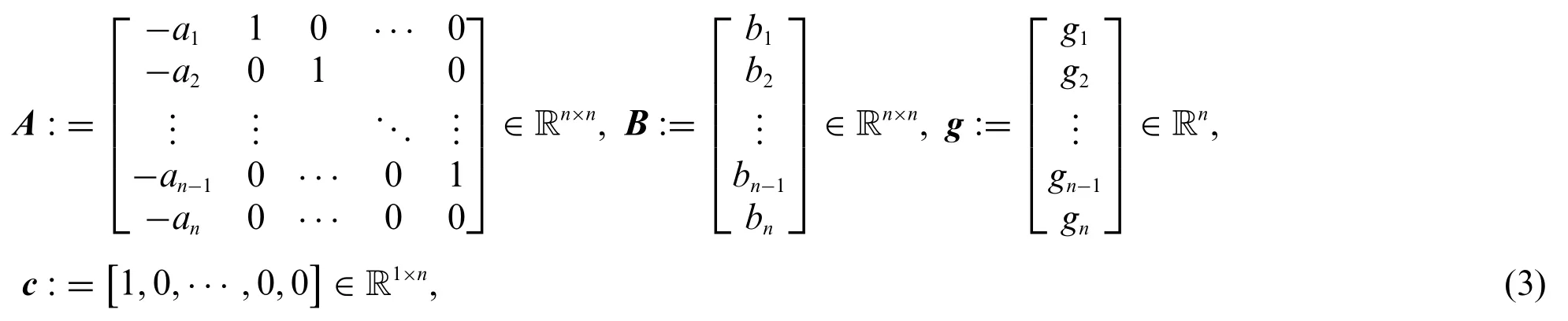
wherebj:=[bj1,bj2,...,bjn]∈R1×n,j=1,2,...,n.

Assumption 1:The dimensionnof the system state vector is known,ut=0,xt=0,yt=0,wt=0 andvt=0 fort≤0.

Assumption 2:The bilinear system in Eqs.(1)and(2)is observable and controllable.

Eq.(1)can be written as

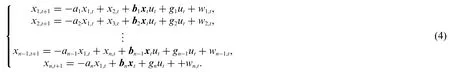
Adding both sides of the above equations has

Substituting Eq.(5)into Eq.(2)obtains the regression form of the bilinear state model

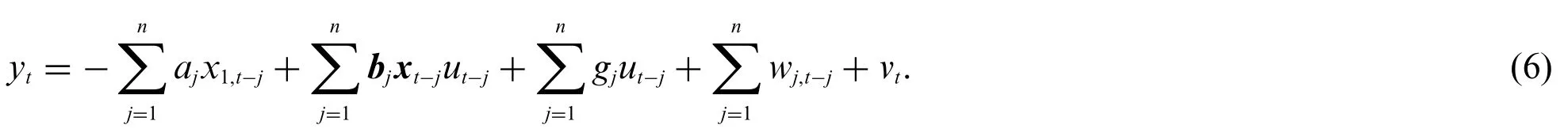
Define the information vectorψtand parameter vectorϑas Redefine the noise term as

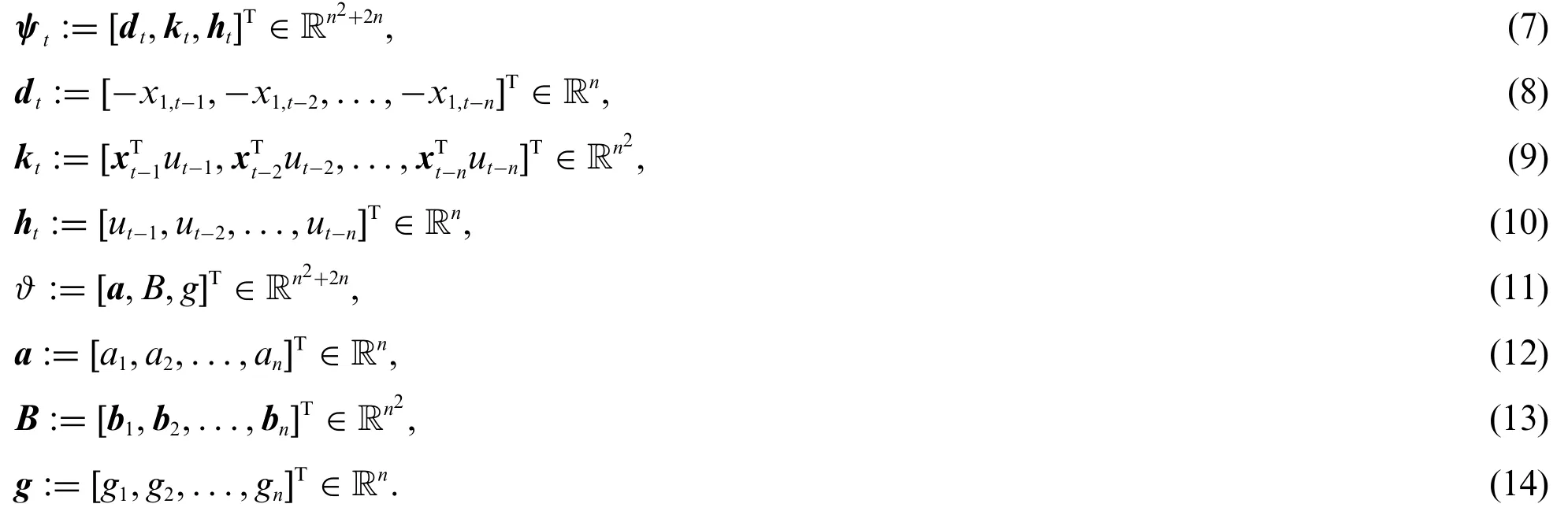
Eq.(6)can be rewritten as

The proposed parameter estimation algorithms in this paper are based on this identification model in (16).Many identification methods are derived based on the identification models of the systems[34–43]and these methods can be used to estimate the parameters of other linear systems and nonlinear systems[44–50]and can be applied to other fields such as chemical process control systems.The purpose of this paper is to obtain the estimates of the unknown parameters in the bilinear state space model by means of the measurement data{ut,yt}.However,the state space model contains not only unknown parameters,but also unknown state variables.That means the information vectorψtin Eq.(16)contains the unknown state vectorxt-i.Given this,we adopt the state observer for estimating the unknown states variables [51].According to the bilinear state space model,the state observer is designed as

where

Remark 1:Differently from the identification of bilinear-in-parameter systems which involve the product terms of the parameter vectors and the information matrices,this paper studies the identification problem of bilinear state-space systems with the product terms of state variables and control variables,which makes it difficult for the parameter and state estimation.

3 Bilinear State Observer Based Continuous Mixed p-norm Gradient Iterative Identification Algorithm

Set the data length beL,based on the input and output data{ut,yt,1≤t≤L},define the stacked input vectorYLand the stacked information matrixΨLas

To suppress the effect of noise interference,define the continuous mixedp-norm cost function

whereλ(p)is the probability density-like weighting function which is constrained byandVL:=YL-ΨLϑ.

Using the negative gradient search method to minimize the cost functionJ1(ϑ)with respect toϑgives

where

Therefore,Eq.(19)can be expressed as

where

Lets= 1,2,3,...be the iteration variables,be the parameter estimation vector at iterations.Using the negative gradient search and minimizingJ1(ϑ)yield

whereμsis the iteration step size[52–57],which satisfies

Eqs.(21)and(22)cannot figure out the parameter estimation vector,because the information matrixΨLcontains the unknown statesxt-j.The solution is to replace the unknown statesxt-jin the information matrix with their estimates obtained by the state observer at the previous iteration.Define the estimated information matrix as

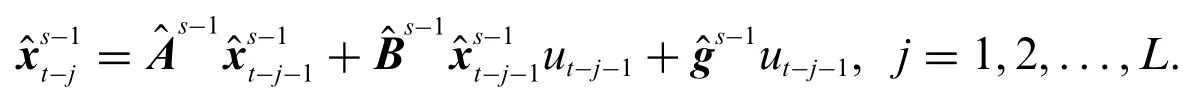
Replace the information matrixΨLin Eqs.(21)and(22)with its estimated value,the estimateat iterationsisReplacingin(20)with its estimates gives

To obtain a closed form formula for,a uniform weighting functionλ(p)= 1 is assumed.Then,the bilinear state observe-based continuous mixedp-norm gradient iterative(BSO-CMPN-GI)identification algorithm(24)–(30)for the bilinear system is summarized in the following:

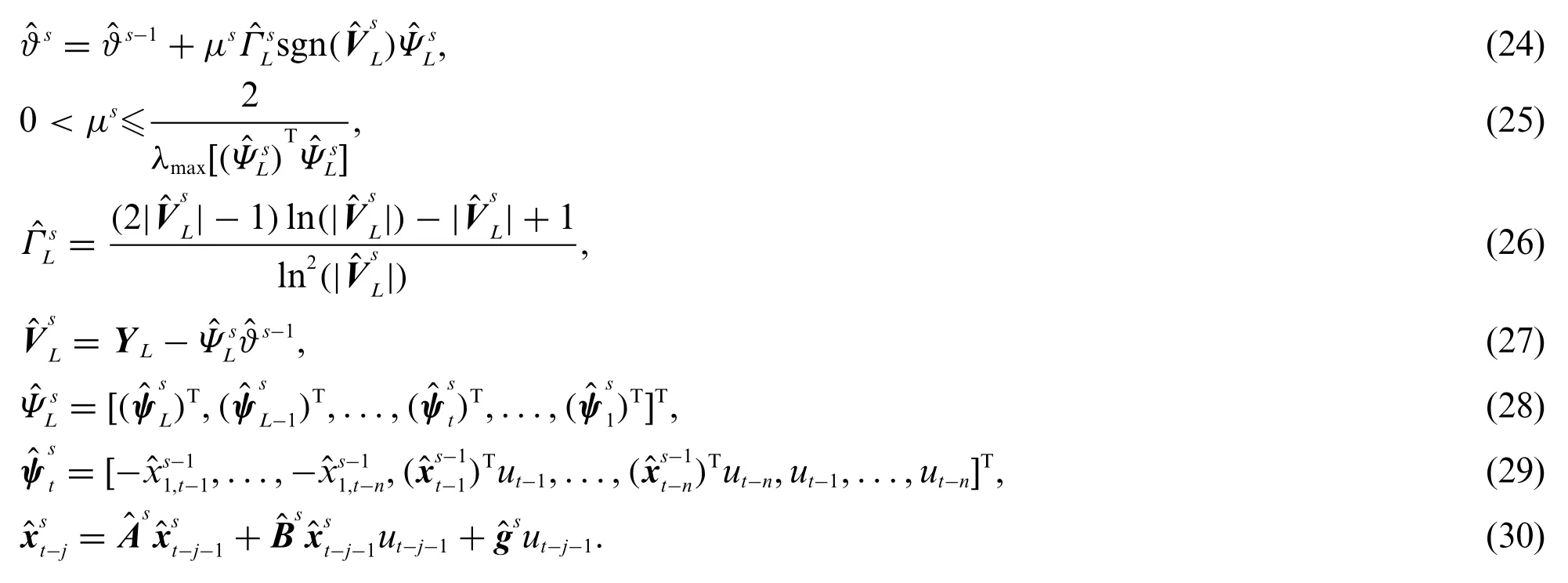
The flowchart of the BSO-CMPN-GI algorithm in Eqs.(24)–(30)is shown in Fig.1.

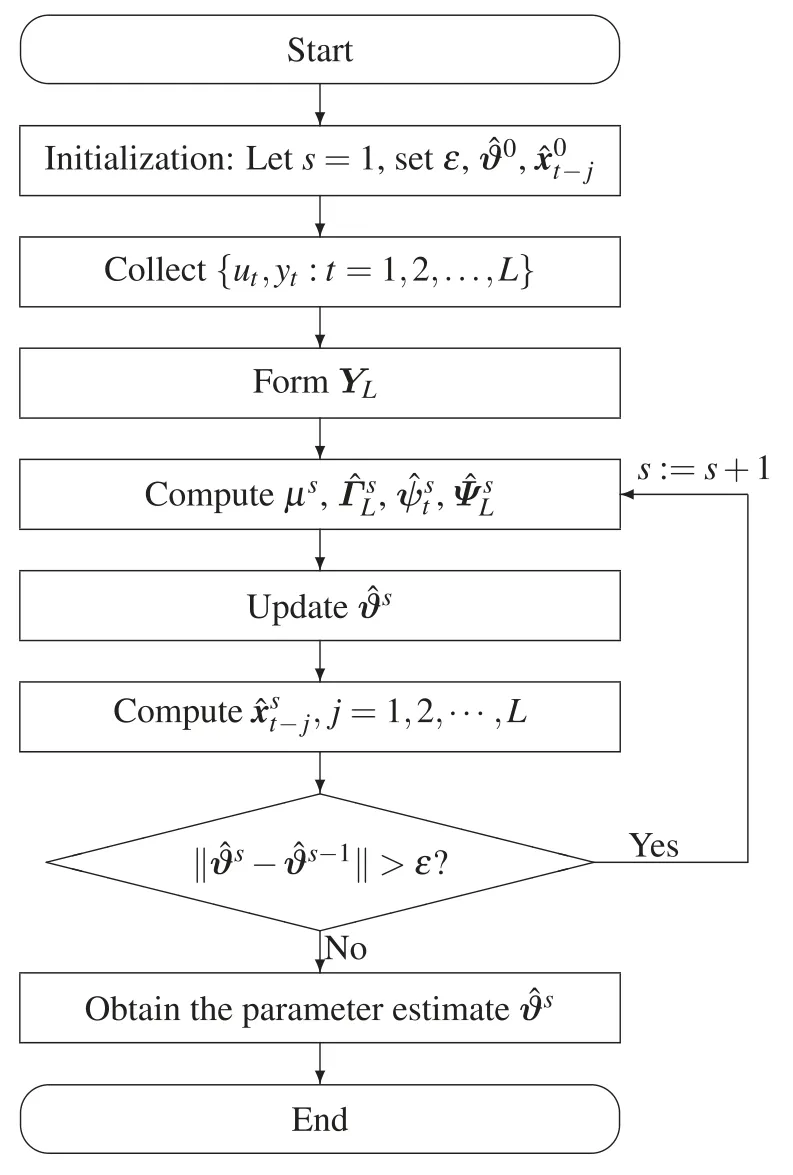
Figure 1:The flowchart of the BSO-CMPN-GI algorithm

Remark 2:The parameterpin BSO-CMPN-GI is adapted by continuousp-norm without resorting to a priori knowledge of the noise.

Remark 3:The BSO-CMPN-GI algorithm makes full use of the measurement data in each iteration of the calculation process,but it requires a batch of data to be collected in advance,and thus is implemented offline.Therefore,an on-line identification algorithm derived from the BSO-CMPNGI algorithm will be introduced by exploiting the past and current measurement data to estimate the unknown parameters in Section 4.

4 Bilinear State Observe Moving Window Continuous Mixed p-norm Gradient Iterative Algorithm

In this section,we introduce the moving window method to derive an on-line identification algorithm and enhance the performance of the BSO-CMPN-GI algorithm.The length of the moving window is set as a fixed valuem.Define the stacked output vectorYt,mand the stacked information matrixΨt,mas

Consider the measurements fromt-m+1 totand define the cost function

where

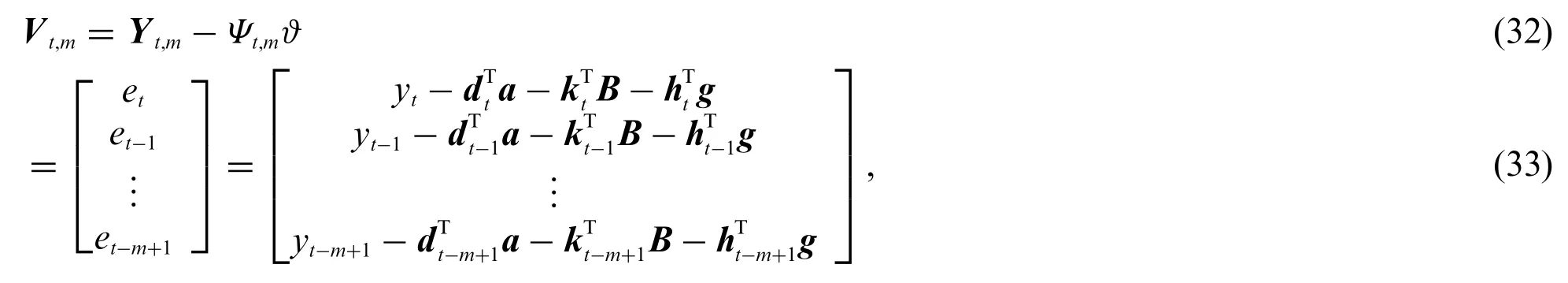
Taking the gradient ofJ2(ϑ)gives

where

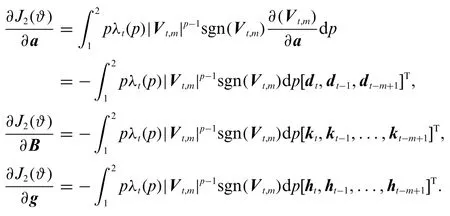
Therefore,Eq.(4)can be expressed as

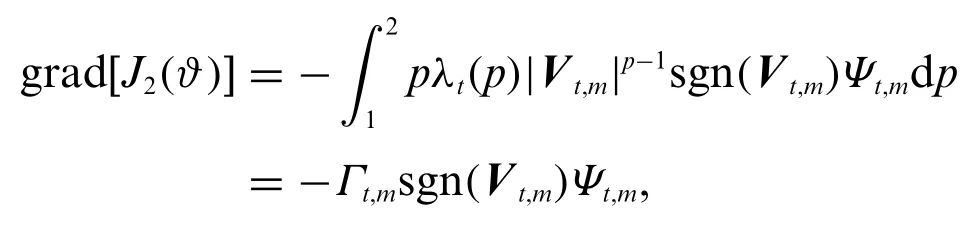
where

Lets= 1,2,3,...be iteration variables.Similar to the derivation of the BSO-CMPN-GI algorithm,using the negative gradient search method and minimizingJ2(ϑ)get

where

As pointed earlier in Section 3,the unknown statesxt-jin the information matrixΨt,mare replaced with their estimates.The estimated information matrixis redefined as

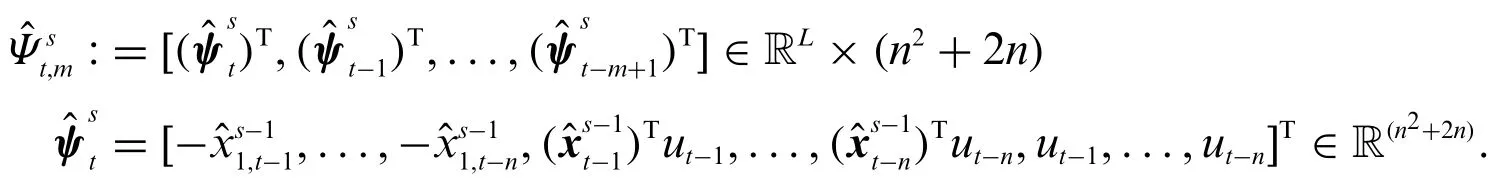
whereis estimated by the state observer:

Based on the above derivation,a bilinear state observe-based moving window continuous mixedpnorm gradient iterative(BSO-MW-CMPN-GI)algorithm proposed for the bilinear state space system is summarized as follows:

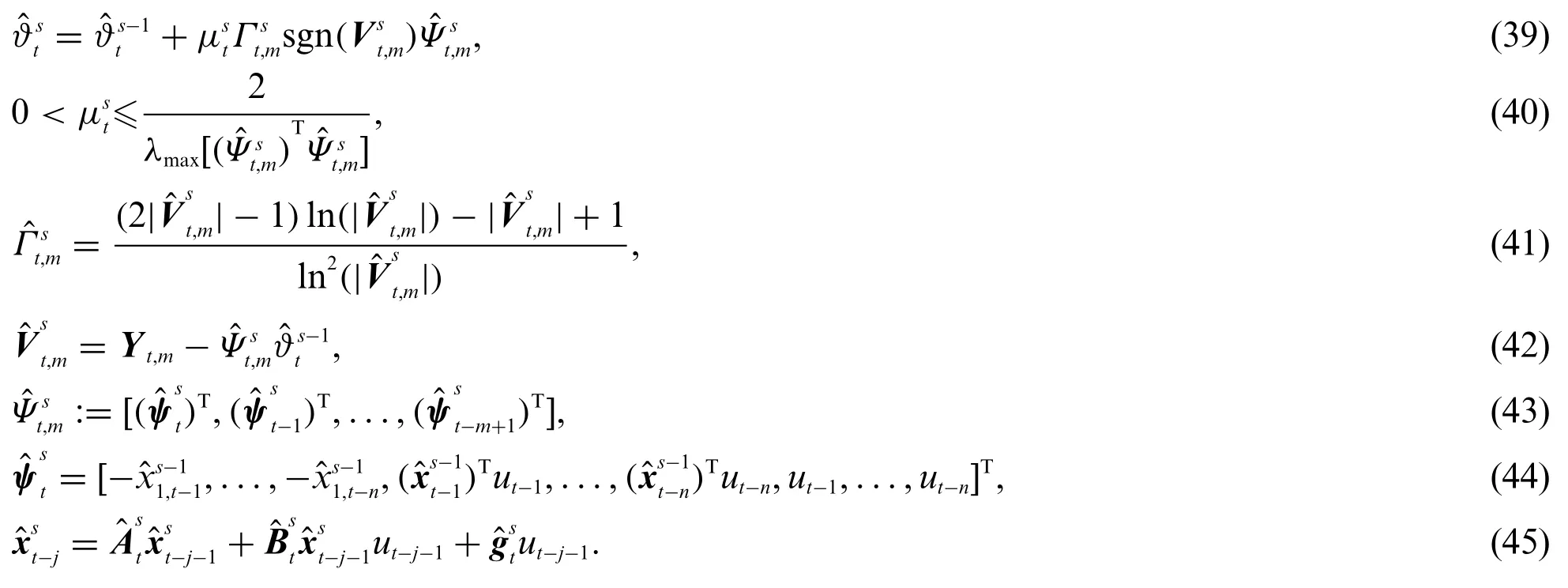
The flowchart of the BSO-MW-CMPN-GI algorithm in Eqs.(39)–(45)is shown in Fig.2.

Remark 4:The parameter estimate given by the BSO-MW-CMPN-GI algorithm depends only on the iterative counters,but also timet.As the sampling timetincreases,the BSO-MW-CMPN-GI algorithm can utilize a batch of data to calculate the parameter estimate simultaneously.

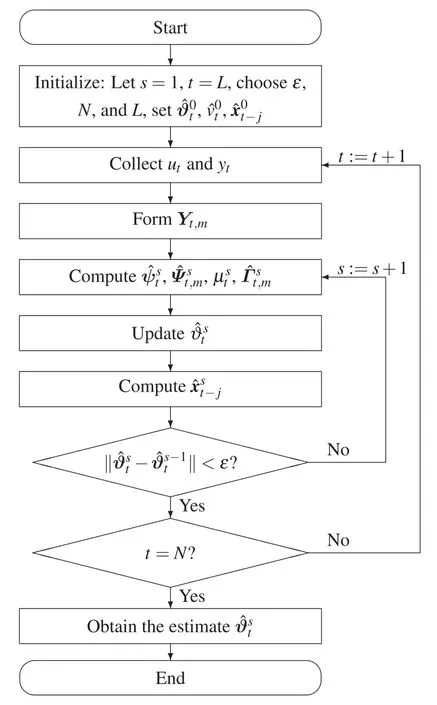
Figure 2:The flowchart of the BSO-MW-CMPN-GI algorithm for computing

5 Simulation

Case 1:About parameter estimation

Consider a second-order bilinear state space system:

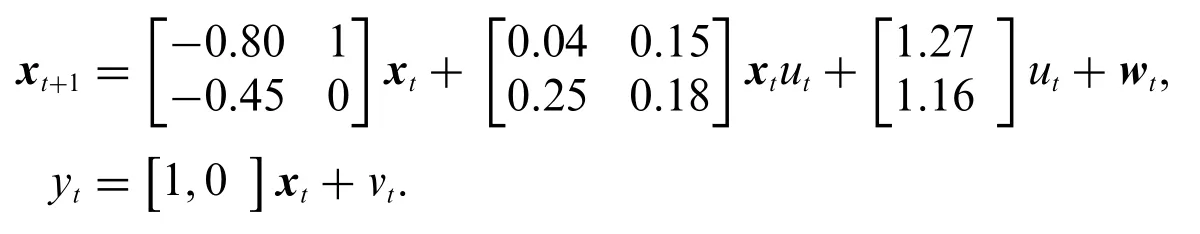
The parameter vector to be estimated is

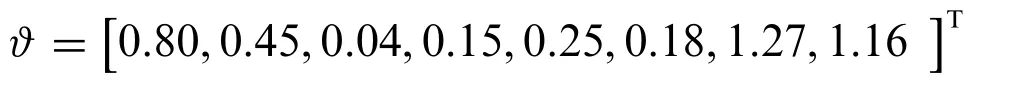
In simulation,the input {ut} is taken as an uncorrelated uniform disturbance random signal sequence with zero mean and unit variance,{wt} is taken as an uncorrelated process white noise vector sequence with zero mean and varianceQ== 0.022,{vt} is taken as a white noise vector sequence with zero mean and variance= 1.002and= 1.502,respectively.Apply the BSO-CMPN-GI algorithm in Eqs.(24)–(30) and the BSO-MW-CMPN-GI algorithm in Eqs.(39)–(45)with the data lengthL=500 to estimate the statesxtand parametersϑof this bilinear system,respectively.For comparison with the different algorithm,we introduce the bilinear state observe-based gradient iterative(BSO-GI)algorithm.In the BSO-MW-CMPN-GI algorithm,s=15 represents the iteration variable,andm=60 represents the recursive variable.The parameter estimates and errorsδ:=-ϑ‖/‖ϑ‖vs.sof the BSO-GI algorithm,the BSO-CMPN-GI algorithm and the BSO-MW-CMPN-GI algorithm with different noise variances are shown in Tables 1 and 2.The parameter estimation errorsδ vs.sof the BSO-GI algorithm,the BSO-CMPN-GI algorithm and the BSO-MW-CMPN-GI algorithm with different noise variances are shown in Figs.3–6,respectively.The estimated output (EO) and the actual output (AO) of the four algorithms are shown in Figs.7 and 8.From Tables 1 and 2 and Figs.3–8,the following conclusions can be drawn:

· The parameter estimation errors given by the BSO-GI algorithm,the BSO-CMPN-GI algorithm and the BSO-MW-CMPN-GI algorithm become smaller as the iterationsincreases.It thus to say the proposed algorithms are effective for bilinear systems.

· The state estimates are close to their true values withtincreasing.

· Under the same data length,a lower noise variance leads to higher parameter estimation accuracy by the BSO-GI algorithm,the BSO-CMPN-GI algorithm and the BSO-MW-CMPNGI algorithm.

· The BSO-CMPN-GI algorithm and the BSO-MW-CMPN-GI algorithm possess higher parameter estimation accuracy at the same noise variance compared with the BSO-GI algorithm.

· When comparing the BSO-CMPN-GI algorithm and the BSO-MW-CMPN-GI algorithm,the parameter estimation errors of the BSO-MW-CMPN-GI algorithm become smaller withmincreasing,and approach to zero ifmis large enough.

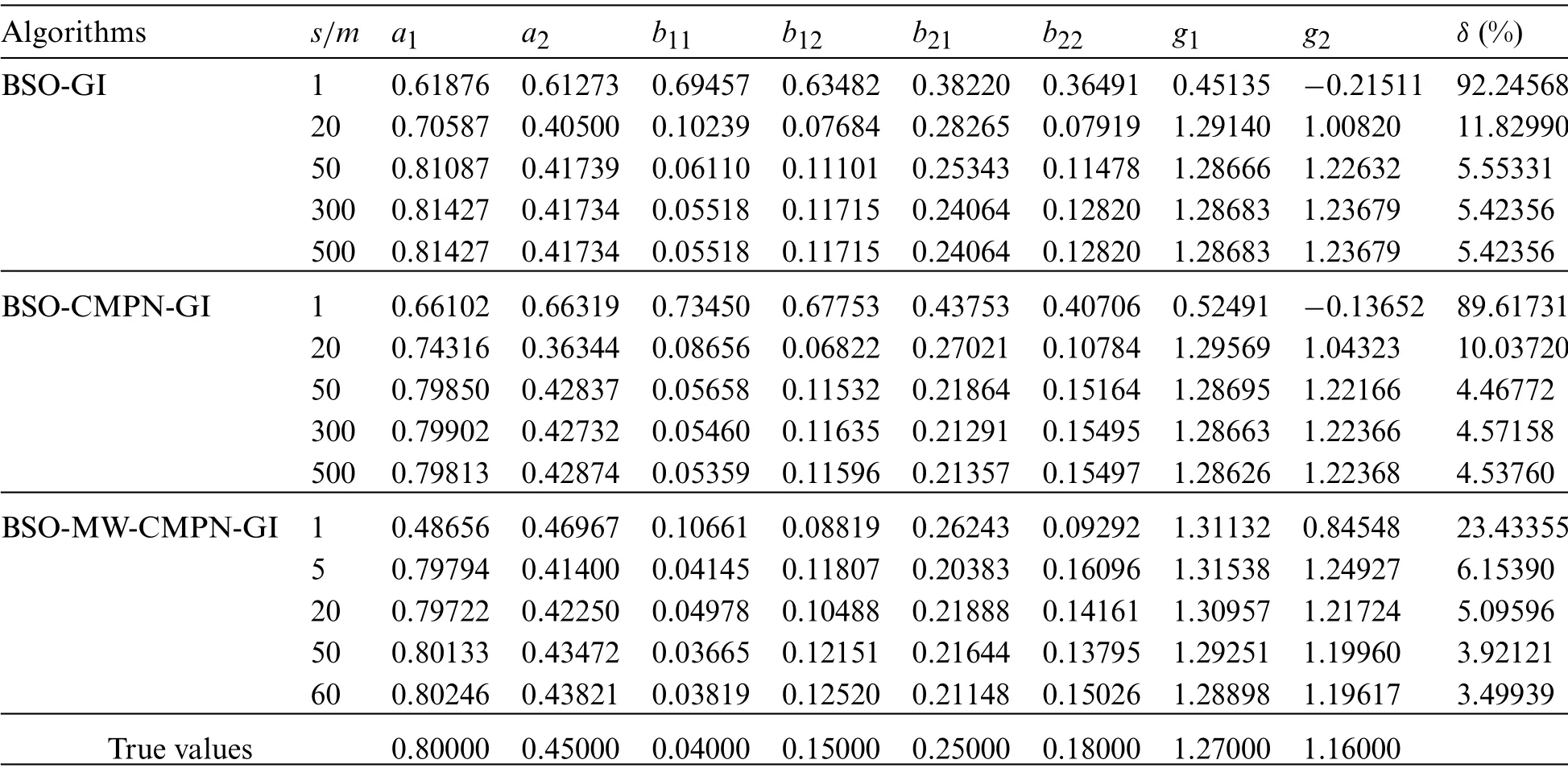
Table 1: The parameter estimates and errors with σ2 =1.002

Table 2: The parameter estimates and errors with σ2 =1.502

Table 2 (continued)

Figure 3:The estimation errors δ vs.t with σ2 =1.002

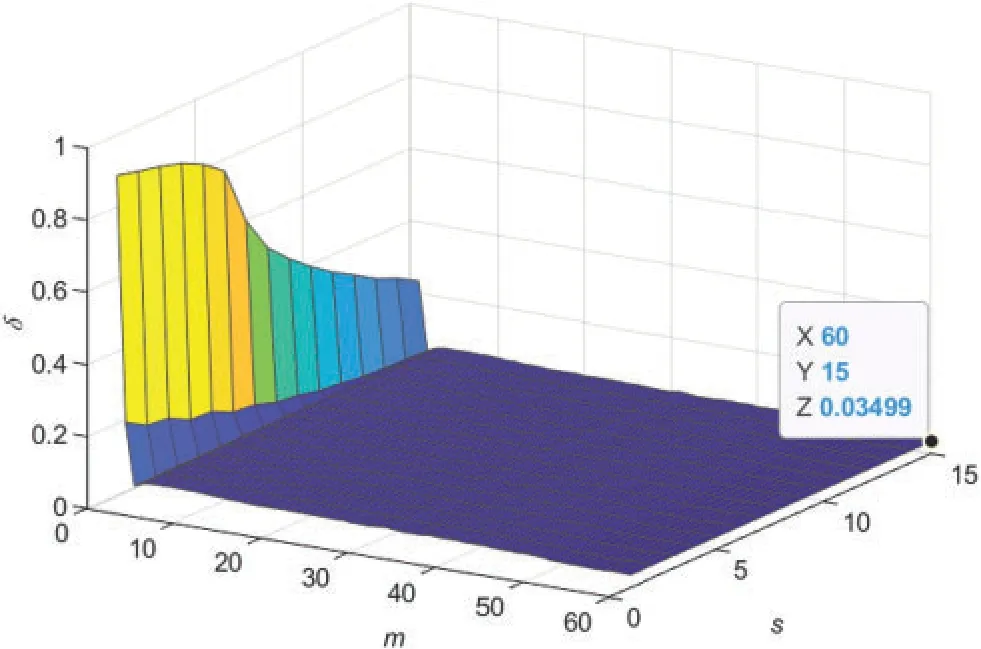
Figure 4:The BSO-MW-CMPN-GI estimation errors δ vs.m and s(m=60 and s=15)with σ2 =1.002

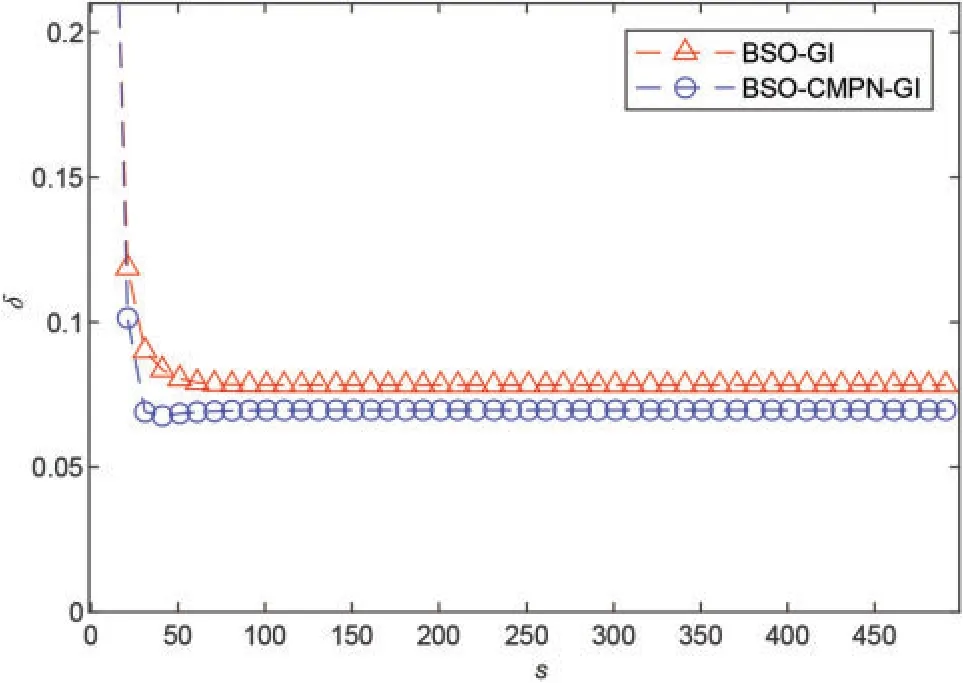
Figure 5:The estimation errors δ vs.t with σ2 =1.502

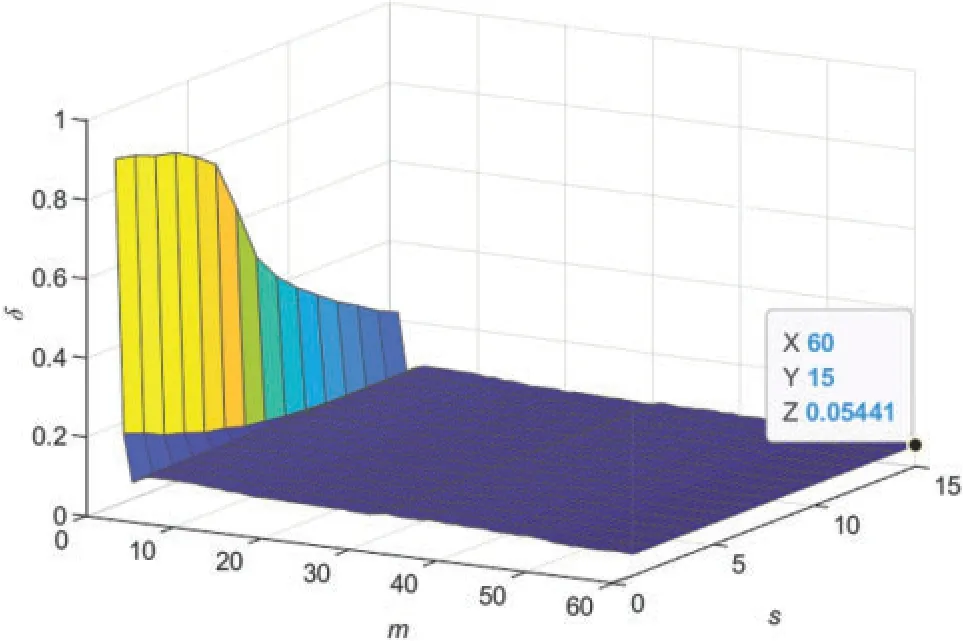
Figure 6:The BSO-MW-CMPN-GI estimation errors δ vs.m and s(m=60 and s=15)with σ2 =1.502

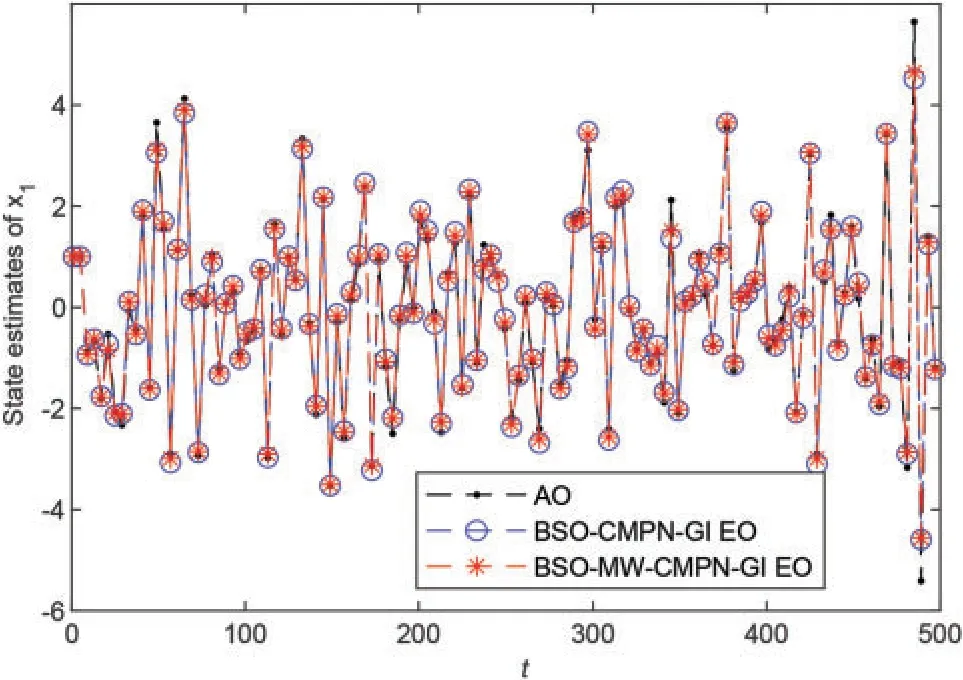
Figure 7:State x1,t and the estimated state vs.t

Figure 8:State x2,t and the estimated state vs.t

Case 2:About model validation

Applying the BSO-CMPN-GI algorithm and the BSO-MW-CMPN-GI algorithm to construct the estimated model for the model validation,respectively.Take the data fromt= 1001 tot= 2000 to calculate the root mean square errors(RMSEs)of the predicted output.Using the BSO-CMPNGI and BSO-MW-CMPN-GI estimates in Table 1 with the noise variance= 1.002.The actual output (AO)ytand the predicted output (PO)are plotted in Fig.9.The RMSEs of the BSO-GI,BSO-CMPN-GI and BSO-MW-CMPN-GI are

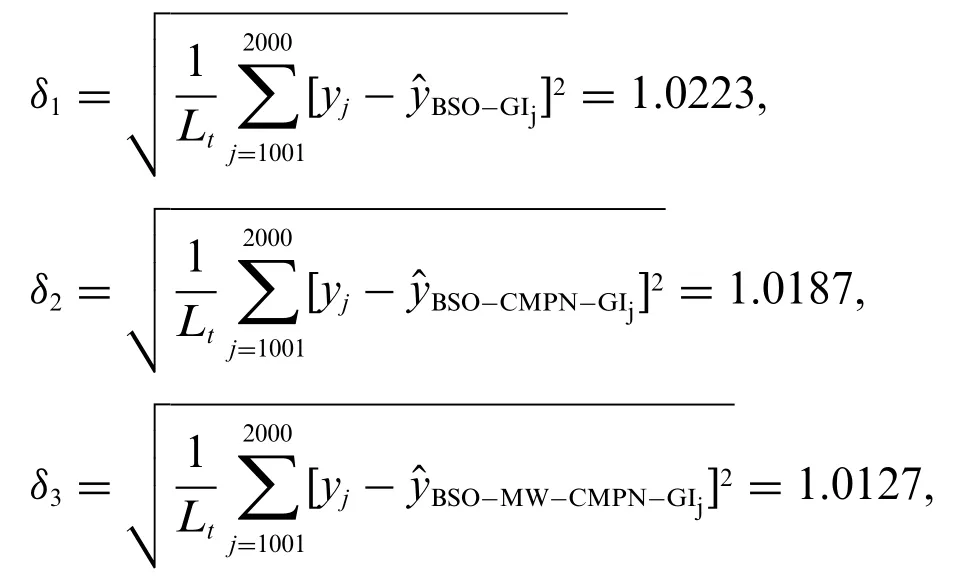
From Fig.9,we can see that the predicted outputs of the BSO-CMPN-GI and the BSO-MWCMPN-GI are very close to the true outputs,and the RMSEs of the two algorithms are very close to the noise standard deviation=1.002.In other words,the estimated model can capture the dynamics of the system.

Figure 9:The system actual outputs and the predicted outputs vs.t with=1.002

6 Conclusions

This paper studies the parameter identification problems of the nonlinear systems described by the bilinear state space models with the noise disturbances.A bilinear state observe-based continuous mixedp-norm gradient iterative algorithm and a bilinear state observe-based moving window continuous mixedp-norm gradient iterative algorithm are proposed to estimate the parameters of the bilinear system.The proposed optimal algorithms are robustness for stochastic white noise by means of the continuously mixedp-norms theory.In order to improve the performance of the proposed algorithms,the moving window identification theory is introduced into the proposed algorithm.Although the proposed algorithms are effective for identifying the bilinear system,it also has some limitations.For example,the disturbance noise is confined to the white noise.The proposed model parameter estimation methods in the paper can combine some mathematical strategies [58–60] and other estimation algorithms [61–65] to study the parameter identification problems of linear and nonlinear systems with different disturbances[66–68]and can be applied to other fields[69–74]such as engineering application systems.

Funding Statement:This research was funded by the National Natural Science Foundation of China(No.61773182)and the 111 Project(B12018).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.