冗余机械臂轨迹的增广Lagrange−改进粒子群算法优化

吴国强

（湖州职业技术学院，浙江湖州 313000）

1 引言

冗余机械臂可以实现机械臂对避障、避奇异、容错控制等特殊需求，但是其运动学逆解和轨迹优化研究也带来了困难。

机械臂不同的运动轨迹具有不同的平滑性和冲击性，进而影响机械臂的驱动能耗、工作效率、使用寿命、运行平滑性和振动性等[1]。因此研究冗余机械臂的轨迹优化问题具有重要的实际应用价值。

机械臂轨迹规划是机械臂运动控制的基础，根据不同的性能需求，轨迹优化指标包括时间最优、能耗最优、冲击最小以及多指标结合的综合优化等[2]。

根据工作空间的不同，机械臂轨迹规划分为笛卡尔空间和关节空间两类[3]，两者之间通过运动学正解和逆解可以相互转换，这里研究的是关节空间轨迹的综合优化问题。

轨迹的综合优化主要包括两种思路，一是使用加权系数法将多个目标转化为单目标优化问题，通过调整不同目标的权系数来调整优化重心[4]；二是使用非支配排序思想得到Pareto前沿解[5]，而后依据优化需求从Pareto解集中选择优化解。本质上讲，两种优化方法均存在优化取舍的过程。文献[6]考虑机械臂运动学、力矩和载荷约束，使用三次多项式作为关节空间基轨迹，使用遗传算法规划了时间最优轨迹，依据实验验证了该方法的有效性。文献[7]考虑机械臂重载情况下的运动约束，使用加权系数法建立了时间−加加速度的综合优化模型，提出了自适应遗传算法的模型求解方法，仿真结果验证了算法的有效性。文献[8]建立了调姿时长和能量消耗的加权目标函数，提出了基于动力学RRT*算法的自由漂浮空间机器人轨迹规划方法，仿真结果表明该方法可以快速地生成自由漂浮机器人的运动轨迹。

总的来说，一般将机械臂轨迹规划问题通过建模转化为带约束的优化问题，而优化算法的优化能力成为决定解质量的关键，因此关于优化算法的研究是机械臂轨迹规划的一个焦点。

这里针对冗余机械臂的轨迹优化问题，建立了以减小工作时间和冲击为目标的优化模型。使用增广拉格朗日乘子法将约束优化问题转化为无约束优化问题，提出了多学习行为粒子群算法的求解方法，达到了减小工作时间和运动冲击的目的。

2 问题描述与建模

2.1 冗余机械臂介绍

这里研究对象为7自由度冗余机械臂，其构型，如图1（a）所示。实物，如图1（b）所示。图中坐标系(x0，y0，z0)为基坐标系，坐标系(xi，yi，zi)，i=1～7为7个关节坐标系，其中坐标系(x7，y7，z7)为机械臂末端执行器坐标系。图1 中参数θi为关节i的转动角度；αi为扭角，表示沿Xi−1轴从Zi−1转动到Zi的角度；ai为连杆i的长度，di为偏置量。

图1 7自由度机械臂构型图Fig.1 The Configuration of the 7−DOF Manipulator

所研究机械臂的构型参数，如表1所示。

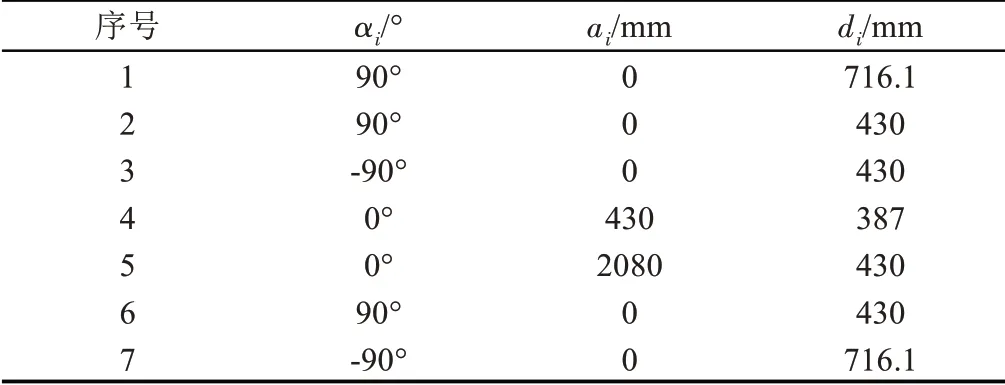
表1 机械臂构型参数Tab.1 The Configuration Parameters of the Manipulator

2.2 问题描述与模型建立

根据机械臂的活动范围、障碍物分布及任务需求，在笛卡尔空间为机械臂规划出若干个必经的轨迹点，记为P0，P1，P2，…，PM，其中P0为机械臂的初始位姿，PM为最终位姿，P1～PM−1为中间轨迹点的位姿。使用文献［9］给出的冗余机械臂逆运动学求解法，可以将笛卡尔空间点转化为关节空间点，记为θ0，θ1，θ2，…，θM。由于研究对象为7自由度机械臂，则每个关节空间点θm由7个关节角组成，记为θm=(θm1，θm2，…，θm7)。

机械臂关节空间轨迹规划描述为：通过优化机械臂到达各轨迹点的时间点tm，m=1，2，…，M，实现机械臂工作时间短和运动冲击小的目标。将关节m的空间轨迹记为Qm(t)，使用加权系数法将两个优化目标转化为一个，为：

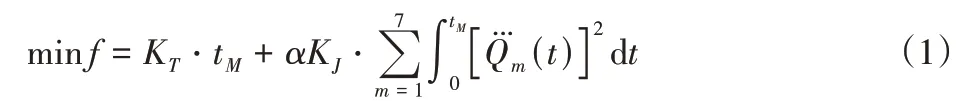
式中：minf—目标函数；KT—时间权值；KJ—冲击权值，且KT+KJ=1；α—调节系数，将时间参数与冲击参数调节在同一数量级；tM—机械臂工作时间；Q…m(t)—轨迹dQm(t)的3 阶导数。

优化的约束条件包括转动角速度约束、转动角加速度约束及转角冲击约束等，即：

式中：Vmmax—关节m的最大转动角速度；Ammax—关节m的最大转动角加速度；Jmmax—关节m可承受的最大转角冲击。

综合式（1）与式（2），即为冗余机械臂轨迹优化的带约束优化模型。

2.3 轨迹插值函数

三次样条插值函数具有简单易实现、可以克服轨迹点间的过度振荡和冲击等优势，因此这里使用三次样条插值函数作为轨迹插值函数。在前文中，M−1 个时间点将[t0，tM]划分为{(t0，t1)，(t1，t2)，…(tM−1，tM)}，共M个时间段。在每个时间段上关节空间轨迹均为三次函数，且满足以下条件：

（1）在每个区间(ti，ti+1)上，S(t)=St(t)均为三次函数；

（2）满足插值条件，即S(ti)=θ(ti)；

则称曲线S(t)为三次样条插值函数。

将S(t)记为一般形式，为：

对于M段插值函数Si(t)，i=1，2，…M，共4M个参数待定，需要4M个方程才能求解。

根据以上4M个等式可以确定4M个未知参数，从而得到三次插值函数。

3 增广拉格朗日−粒子群算法求解

3.1 带约束优化转化为无约束优化问题

将约束优化问题转化为无约束优化问题一般使用罚函数法，但是此方法要求罚因子趋于无穷大或者无穷小才能取得目标函数最值，使得迭代过程收敛较慢，而增广拉格朗日乘子法可以较好解决这一问题，其核心思想是通过构造外点惩罚函数从而将约束优化转化为非约束优化。

这里的约束为不等式约束，因此使用适用于不等式约束的增广拉格朗日乘子法。

首先给出带不等式约束的一般优化模型，为：

式中：J—不等式约束的数量。使用增广拉格朗日乘子法可以将其转化为无约束优化问题，为：

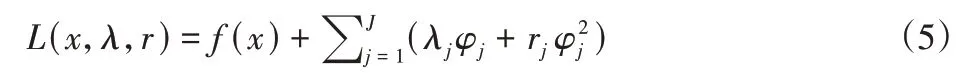
式中：x—优化变量；λj—约束条件j的拉格朗日乘子；rj—约束条件j的惩罚因子，φj表达式为：

结合式（5）和式（6）可以将约束优化问题转化为无约束优化问题。其中拉格朗日乘子λj的迭代公式为：

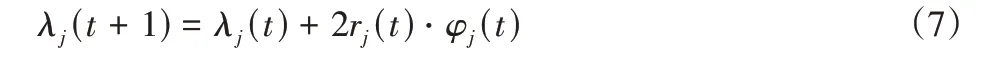
式中：t—迭代次数。惩罚因子rj的迭代方法为：

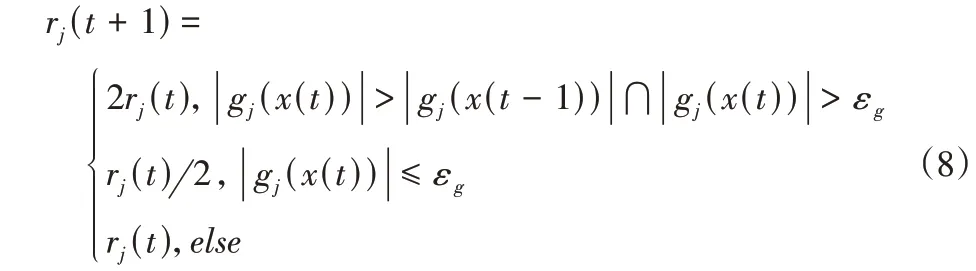
式中：εg—描述约束的误差精度。以上迭代的终止条件为：

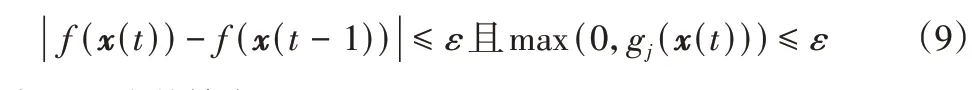
式中：ε—收敛精度。

3.2 多学习行为粒子群算法

将粒子规模记为N，粒子维度记为D，粒子i位置记为Xi=(xi1，xi2，…，xiD)，速度记为Vi=(vi1，vi2，…，viD)，粒子i的历史最优位置记为Pi=(pi1，pi2，…，piD)，粒子群体的最优位置记为Pg=(pg1，pg2，…，pgD)，则粒子i搜索过程描述为［10］：

式中：ω—运动惯性；t—迭代次数；

c1、c2—自身学习因子和种群学习因子；

r1、r2—（0，1）间随机数。

参考生物进化论的思想可知，单一的物种进化方式会极大地降低物种多样性，从而使算法失去进化能力。为了解决单一进化带来的问题，这里提出了多样的进化方式。

（1）依据群体认知获得进化方向，此时将种群质心位置作为一个进化方向，为：

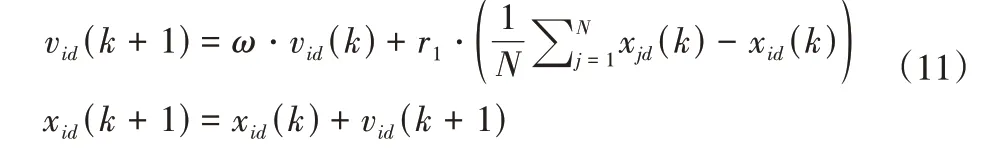
分析式（11）可知，粒子在自身惯性和质心引导之下进行搜索。

（2）从种群最优和其他粒子中获得进化方向，此时适用于较差粒子，因较差粒子位置不具备参考价值，因此取消惯性作用，为：

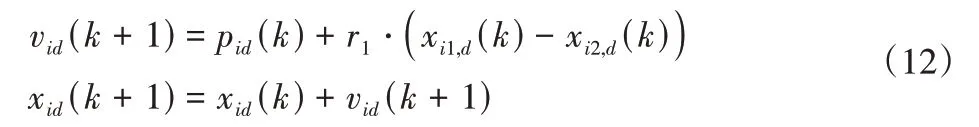
式中：i1、i2—种群中任意不相同的两个个体。

（3）以差分方式从其余粒子中获得进化方向，即：

式中：i1、i2、i3—种群中任意不相同的三个个体。

3.3 学习行为的价值和选择

在前文中，新定义了3种粒子学习行为，加上传统的学习行为，共4种粒子学习行为。每种学习行为的价值依据目标函数值的减少率定义，为：

式中：Vij(k)—粒子i选择学习行为j的价值；

fj—学习行为j的目标函数。

依据各学习行为的价值构造学习行为的选择概率，为：

式中：Pij(k)—粒子i选择学习行为j的概率；

Pmin—最小选择概率，此参数设置目的是防止某一学习行为的被选概率为0。

按照式（15）计算各学习行为被选概率，按照轮盘赌的规则确定最终选择的学习概率，这样既能够保证较好学习行为具有最大被选概率，同时能够保证学习行为的多样性，从而促进粒子的多样性。

3.4 增广拉格朗日-粒子群算法求解流程

按照增广拉格朗日乘子法和多学习行为粒子群算法的原理，制定基于拉格朗日—粒子群算法的求解流程，如图2所示。

图2 求解流程图Fig.2 Solving Flow

4 实验验证

4.1 实验条件设置

以2.1节介绍的机械臂为实验对象，根据任务需要、机械臂活动范围及障碍物分布，设置7个机械臂的空间轨迹点，如表2所示。由表2中数据可知，关节2和关节6的关节角未发生变化，为锁死状态。

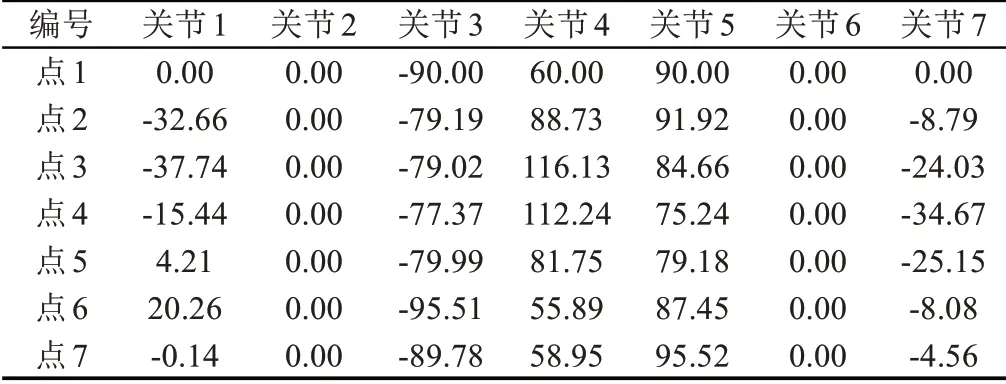
表2 关节空间轨迹点Tab.2 Trajectory Points of Joint Space

关节运动能力参数为：Vmax=3°/s、Amax=3°/s2、Jmax=5°/s3。

拉格朗日乘子初值为：λj=0，j∈[1，7]，初始罚因子为：rj=1000，j∈[1，7]，约束误差精度为：εg=10−4，收敛精度为：ε=10−4。粒子群算法最大迭代次数为：Kmax=100，粒子数量为40。

4.2 实验结果与分析

机械臂的最大运行时间为150s，为了进行比较，本文同时使用增广拉格朗日乘子法−传统粒子群算法、增广拉格朗日乘子法−多学习行为粒子群算法对优化模型进行求解。

KT取1.0，0.5，0等3种情况，KJ取相应值，α=100。以KT=1为例，此时为纯时间优化，粒子群算法与多学习行为粒子群算法的求解过程，如图3所示。

在图3中，传统粒子群算法的收敛次数为62次，最优结果为74.92s；多学习行为粒子群算法的收敛次数为33次，最优结果为73.21s，以上数据说明多学习行为粒子群算法的收敛速度和求解结果均优于传统粒子群算法。

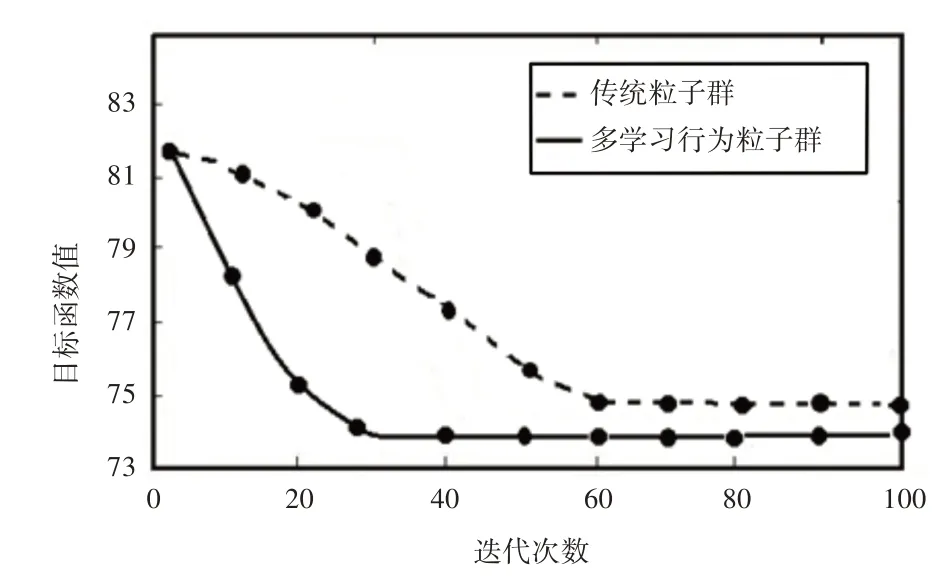
图3 两种算法的求解程Fig.3 Solving Process of the Two Algorithms

统计KT取1.0，0.5，0等3种情况下，粒子群算法和多学习行为粒子群算法的优化结果，如表3所示。

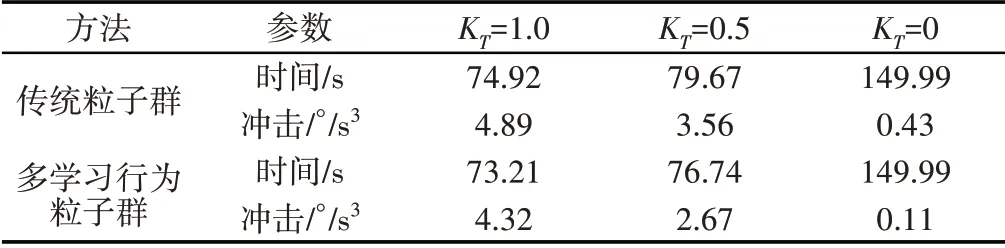
表3 优化结果统计Tab.3 Statistics of the Optimization Result

表3中，当KT=0时为单纯的冲击目标优化，此时粒子群算法和改进粒子群算法都将时间优化为了最大值，从而得到冲击最小值，符合常识。

由表3可知，在KT取1.0，0.5两种情况下，多学习行为粒子群算法优化路径的时间和冲击均小于传统粒子群算法。

结合图3可知，多学习行为粒子群算法的收敛速度也快于传统粒子群算法。

这是因为改进粒子群算法定义了多种粒子的学习行为，并依据各学习行为的价值确定学习行为的选择概率，在保证粒子多样性的同时，能够选择粒子进化最快的学习行为，因此改进粒子群算法的收敛速度和优化结果均好于粒子群算法。

由于篇幅有限，以KT=0.5为例，得到7个关节的角位置、角速度、角加速度、角加加速度曲线，传统粒子群算法规划轨迹，如图4所示。

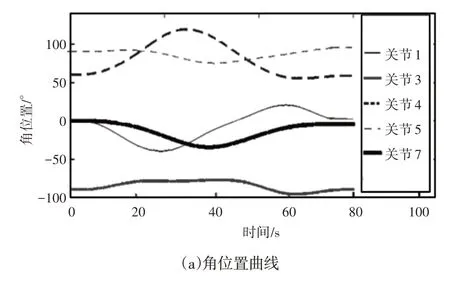
图4 传统粒子群算法的机械臂轨迹Fig.4 Manipulator Trajectory Planned by Traditional PSO

多学习行为粒子群算法规划轨迹，如图5所示。

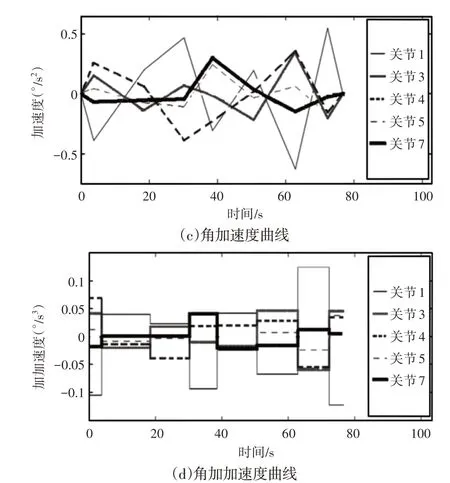
图5 改进粒子群算法的机械臂轨迹Fig.5 Manipulator Trajectory Planned by Improved PSO

由于关节2和关节6为锁死状态，因此关节2和关节6的曲线不再给出。

由图4、图5可以看出，当KT=0.5时，使用传统粒子群算法和多学习行为粒子群算法规划的机械臂关节空间轨迹在角位置、角速度上是平滑的，在角加速度上是连续的。

在角加加速度方面未超出约束范围，满足机械臂关节空间轨迹的可用条件。但是对比图4（d）、图5（d）可知，传统粒子群算法规划的轨迹冲击明显大于改进粒子群算法规划的轨迹，这是因为传统粒子群算法进行轨迹规划时陷入了局部最优，优化不够彻底，而改进粒子群算法兼顾了算法多样性和收敛性，优化能力强于传统粒子群算法。以上优化轨迹和统计参数表明，基于增广拉格朗日−多学习行为粒子群算法的机械臂轨迹优化方法是有效的，且规划效果较好。

5 结论

这里研究了冗余机械臂的关节空间轨迹优化问题，使用加权系数法将多个优化目标统一为单个优化目标，使用增广拉格朗日乘子法将约束优化问题转化为无约束优化问题，提出了多学习行为粒子群算法的求解方法。经过验证可以看出，多学习行为粒子群算法的规划速度和优化结果好于传统粒子群算法，且多学习行为粒子群算法规划的轨迹平滑可用。