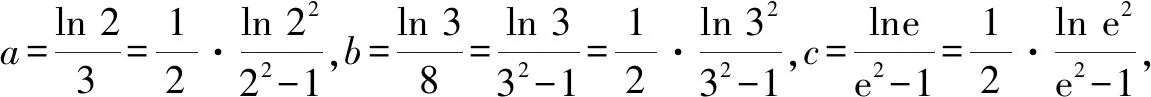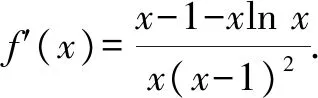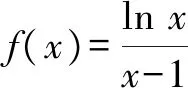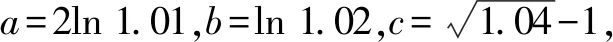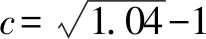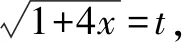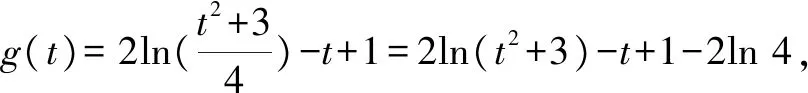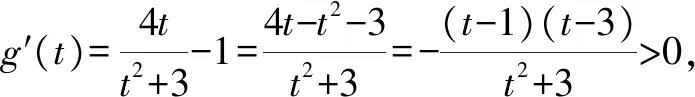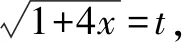用数学抽象解高考试题
——以2022全国新高考Ⅰ卷第7题为例
王光华 孟 泰
江苏省泰州市姜堰区罗塘高级中学 江苏省泗洪县第一高级中学
2022年高考数学全国新高考Ⅰ卷普遍认为是最难的.而选择题第7题又是这份试卷难题的代表.
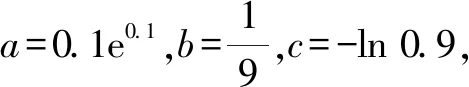
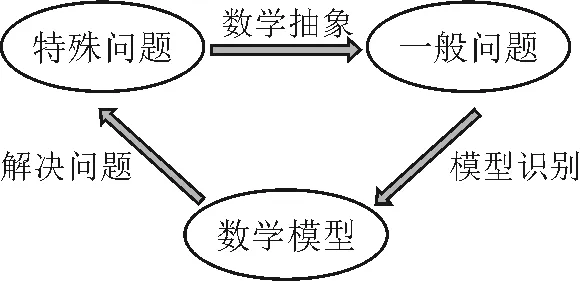
A.a C.c 其实这道题并不难,我们只要在计算器上分别算出a,b,c的值就一见分晓,大小立见. 本题也可以利用泰勒展开式估算其大小,但属于高等数学范畴,普通高中不作要求,有的同学估计没学.因而我们必须另辟蹊径,寻找适合高中 生的解题办法. 先看下面这个问题: 4×34+1是合数吗? 经计算,4×34+1=325,再对325进行分解,325=25×13,所以4×34+1是合数.如果将3改为2 022,那么4×2 0224+1为合数吗?很显然,运用上述方法,运算量大,分解有难度. 因此要换一种思路,这个思路就是抽象.我们将数字3,2 022等数抽象为字母m(m>1,m∈N),问题就抽象为“4m4+1是合数吗”.此时我们很容易想到数学上处理代数式的“因式分解”. 事实上,4m4+1=4m4+4m2+1-4m2=(2m2+1)2-4m2=(2m2+1+2m)(2m2+1-2m). 因而4m4+1为合数.此时只要令m=2 022,就知道4×2 0224+1为合数. 这就是抽象的神奇之处[1]! 在这里,我们先将特殊的数式抽象为具有一般性的代数式,通过模式识别,运用多项式的理论——因式分解,从而解决了这个“4×2 0224+1为合数吗?” 现实世界有很多具体的、特殊的问题.我们就要把它们抽象成一般性的数学问题,然后通过模型识别,寻找解决数学问题的数学模型,从而解决具体的、特殊问题[2].具体思维策略如图1所示: 图1 思维策略 例如:周期现象通过抽象,可以用三角模型解决;随机现象通过抽象,可以用概率统计解决;大小现象通过抽象,可以用函数性质解决. 将0.1记为x(抽象),构造函数: 此时可以通过研究上述三个函数,利用函数单调性比较大小,这是高中常用的方法. (1)先研究a与b的大小 令u(x)=ex(1-x)2-1,求导,可得u′(x)=ex·(x2-1).当x∈(0,1)时,u′(x)=ex(x2-1)<0,则u(x)=ex(1-x)2-1在(0,1)单调递减. (2)再研究a与c的大小 令m(x)=xex-[-ln(1-x)]=xex+ln(1-x),x∈(0,1),则 其分母恒大于零,只需判断分子符号,因此构建函数v(x)=(1-x2)ex-1,x∈(0,1). 所以v′(x)=(1-2x-x2)ex>0 在(0,0.25) 上恒成立. (关键在于选择恰当区间来卡0.1即可.) 于是v(x)在区间(0,0.25) 上单调递增. 所以v(x)=(1-x2)ex-1>v(0)=0, 对∀x∈(0,0.25)恒成立. 所以m(x)=在(0,0.25)上单调递增,从而m(0.1)>m(0)=0,即0.1e0.1>-ln 0.9.故a>c.结合a 数学解题追求大道至简,能否将解题过程简化呢?我们还可以优化以上解题过程. 由于这两个函数解析式的分子相同,因此只要比较分母大小.根据指数切线不等式ex≥x+1,有e-x≥-x+1,当且仅当x=0时等号成立,记x∈(0,1). 再考察b,c的大小关系. 对于x=0.1,则h(0.1) a与c的大小同上,不难看到其运算量较大,能否将a与c的大小比较进行优化呢? 构造函数优化2:利用指数切线不等式ex≥x+1,有e0.1>0.1+1=1.1. 所以a=0.1e0.1>0.1×1.1=0.11. 而c=-ln 0.9如何处理呢? 因此,c=-ln 0.9<0.11 综上c 我们再向教材寻根:通过所给具体数值的特征,抽象出一般性的函数,再根据函数的性质比较具体数值的大小,这在教材中是常见的.例如苏教版必修一第145页的例2. 比较log23.4与log23.8的大小. 解:考察对数函数y=log2x. 因为2>1,所以y=log2x在(0,+∞)上是增函数. 又因为0<3.4<3.8,所以log23.4 从教材给出的例题可以看到,根据所给数据的特征,找出他们的共性特征(同底数、同指数、同真数等),找出他们的相异特征(底数不同、指数不同、真数不同等),构建相应的函数,利用函数的单调性来比较所给数据的大小. 那么数的大小比较问题是否一定运用上述思维策略,即先通过数学抽象,再寻找数学模型来解决呢? 上述高考题的分析,其具体思维导图如图2所示. 图2 综上,思路一通过计算比较大小,虽然思路简单,但受高考及能力限制,不是行之有效.而思路二则是通过观察特殊数的特征抽象出一般意义的函数,利用模型函数的单调性,从而解决了数的大小比较问题. A.c>a>bB.a>c>b C.a>b>cD.c>b>a 思路分析:通过观察三个数的特征,统一形式为 又g′(x)=-lnx<0恒成立,所以g(x)在[4,9]上单调递减,从而g(x) 故a>c>b,答案选:A. 再例如2021年全国卷乙卷理科第12题: A.a C.b 思路分析:从三个数字特征来看,不妨将0.01抽象成变量x,则 a=2ln 1.01=2ln(1+0.01)→2ln(1+x), b=ln 1.02→ln(1+2x), 所以由g(t)>g(1)=2ln 4-1+2ln 4=0. 因此f(x)>0,可得a>c. 于是h(x)<0,即c>b,从而a>c>b.故选:B. 基于2022年高考试题特点,可以看出数学抽象是高考必考查的核心素养,为此在平时学习中我们要: 学会用抽象的眼光观察数学, 学会用抽象的思维思考数学, 学会用抽象的语言表达数学.1 题目的高等数学背景分析
2 解题的一般化思路理解
3 基于数学抽象策略的问题解决


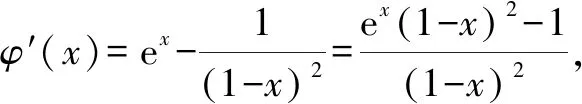
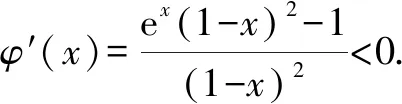
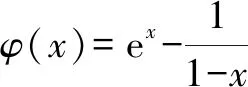
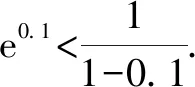
4 解题过程的再优化
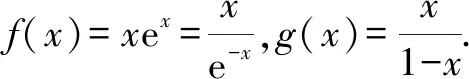
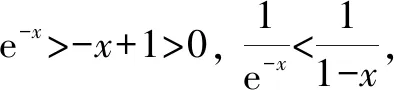

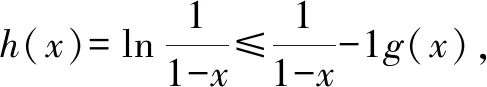

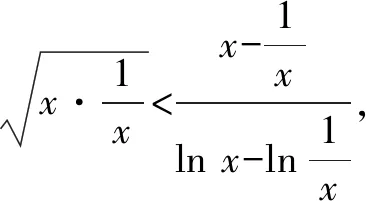
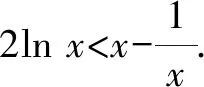
5 思路方法的课本寻根