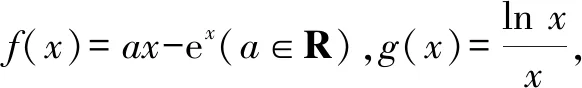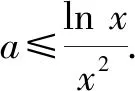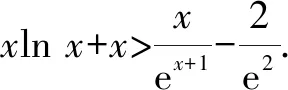浅探“任意性”或“存在性”问题的解法
徐清杰
山东省惠民县第一中学
近几年来,高考数学试题及各省市模拟题中,含逻辑量词的“任意性”或“存在性”问题多有出现,涉及此类问题,学生们多有困惑,现结合个人的教学体会,将其整理归纳为五种情形,与大家共同探讨此类问题的解法,以便于今后的学习实践.
1 一个“任意”、一个“存在”,两个不同函数
此类试题的特点是含有一个“任意”和一个“存在”,分属两个不同的变量,来自两个不同的范围(有时两个范围也可以相同),分别针对两个不同的函数.

分析:题中的“存在”“任意”等价于:f(x)中至少存在一个x0使得f(x0)小于g(x)值域中的任意一个实数,即f(x)min 归纳:(1)∀x1∈D1,∃x2∈D2,f(x1)≥g(x2)成立,则f(x)min≥g(x)min.(适用于f(x),g(x)最值存在的情况,以下同.) 剖析:① 若f(x)的最小值不存在,f(x)∈(m,n),则m≥g(x)min;②若g(x)的最小值不存在,g(x)∈(m′,n′),则f(x)min>m′;③若f(x),g(x)的最小值同时不存在,则m>m′.(注:若f(x),g(x)的最小值不存在时,可以用其值域的左端点替代,但需要验证等号是否能取到.) (2)若∀x1∈D1,∃x2∈D2,f(x1)≤g(x2)成立,则f(x)max≤g(x)max. 剖析:若f(x),g(x)的最大值不存在时,可以用其值域的右端点替代,同样需要验证等号是否能取到,情况与上述剖析类似,不再一一阐述. (3)若∀x1∈D1,∃x2∈D2,f(x1)=g(x2),则f(x)的值域是g(x)的值域的子集. 此类试题的特点是含有两个“任意”,分属两个不同的变量,来自两个不同的范围(有时两个范围也可以相同),分别针对两个不同的函数. 分析:题中两个“任意”,说明f(x)的值域中任意一个实数都不小于g(x)值域中任意一个实数,即f(x)min≥g(x)max. 故a的取值范围为[1,+∞). 归纳:(1)若∀x1∈D1,∀x2∈D2,f(x1)≥g(x2)成立,则f(x)min≥g(x)max. (2)若∀x1∈D1,∀x2∈D2,f(x1)≤g(x2)成立,则f(x)max≤g(x)min. 此类试题的特点是含有两个“存在”,分属两个不同的变量,来自两个不同的范围(有时两个范围也可以相同),分别针对两个不同的函数. 故a的取值范围为(-2,0). 归纳:(1)若∃x1∈D1,∃x2∈D2,f(x1)≥g(x2),则f(x)max≥g(x)min. (2)若∃x1∈D1,∃x2∈D2,f(x1)≤g(x2),则f(x)min≤g(x)max. (3)若∃x1∈D1,当x2∈D2,f(x1)=g(x2),则f(x)的值域与g(x)的值域的交集是非空集. 点评:此类两个不同的x值,满足两个不同函数的求参数范围问题,通常有两种解法.①求出两边各自的最值,再解两最值的不等式,如例1、例3;②有时一边的最值不易求出,而另一边的最值容易求出时,可借助于求出的最值,对不等式进行同解变形,构造一个与背景函数相关的辅助新函数,再将不等式分离参数,如例2;也可对参数进行分类讨论. 此类试题的特点是含有一个“任意”,连接一个变量,分别针对两个不同的函数. 例4已知函数f(x)=ex-1,g(x)=ax2+x,若对任意x∈[0,+∞),f(x)≥g(x)恒成立,求实数a的取值范围. 分析:可先考虑分离参数法;如果参数不易分离,再考虑构造新函数法,即∀x∈[0,+∞),f(x)-g(x)≥0恒成立,令h(x)=f(x)-g(x),只需h(x)min≥0即可. 归纳:(1)若∀x∈D,f(x)≥g(x)恒成立,可先考虑分离参数法;后考虑构造新函数法,设h(x)=f(x)-g(x),则h(x)min≥0. (2)若∀x∈D,f(x)≤g(x),解法同上(或分离参数法;或h(x)max≤0). 此类试题的特点是含有一个“存在”,连接一个变量,分别针对两个不同的函数. 分析:可以先考虑分离参数法解决问题;如果不易分离参数,可直接转化为∃x∈(0,+∞),f(x)-g(x)+ex≤0成立,令h(x)=f(x)-g(x)+ex,则只需证明h(x)min≤0. 归纳:(1)若∃x∈D,f(x)≥g(x)成立,可先考虑分离参数法;后考虑构造新函数法,设h(x)=f(x)-g(x),则h(x)max≥0. (2)若∃x∈D,f(x)≤g(x),解法同上(或分离参数法;或h(x)min≤0). 点评:此类一个x值,满足两个不同函数的问题,若条件中含有参数,需要求参数的取值范围时,可考虑两种解法.①若参数容易分离,可将参数与其他变量分离,构造一个新函数,转变为求新函数的最值,如例5;②若参数不易分离,可通过不等式的同解变形,构造一个与背景函数相关的新函数,常需对参数进行分类讨论,如例4.若证明不等式成立时,通常也有两种证明方法.一是通过不等式的同解变形,将不等式转化为两个函数的最值进行比较,如例6;二是通过不等式的同解变形,构造一个新函数证明不等式,如例7. 总结:两个不同的x值x1,x2针对两个不同的函数f(x1),g(x2)的“任意性”或“存在性”问题,根据上述两个不同x值的不同情况,分别求出f(x),g(x)相应的最值,然后比较大小;有时也会只求一个函数的最值,重新加以整合,或分离参数法,或构造一个新函数进行分类讨论.同一个x值针对两个不同的函数f(x),g(x)的“任意性”或“存在性”问题,根据上述同一个x值的不同情况,或分离参数法,或构造一个关于f(x),g(x)差的新函数,再求相应的最值.Z
2 两个“任意”,两个不同函数


3 两个“存在”,两个不同函数

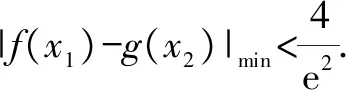
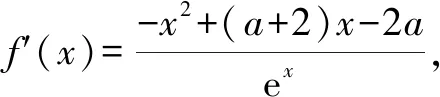
4 一个“任意”,两个不同函数
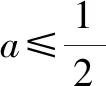
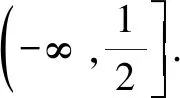
5 一个“存在”,两个不同函数