逻辑方阵构建体系的三大转变
李贤军,邓子燕
(贵州民族大学文学院,贵州 贵阳 550025)
逻辑方阵(logical square)最早是由古希腊哲学家亚里士多德(Aristoteles)奠定思想基础,并“为逻辑方阵的构成作了材料上的整理或准备[1]”。古罗马时期的阿普里乌斯(Apuleius)构建了逻辑方阵的雏形,古罗马晚期哲学家波伊提乌(Anicius Manlius Severinus Boethius)在此基础上构建了完整的逻辑方阵,至今已达1500多年。经前贤的不断探究,特别是近30多年来逻辑方阵研究成果丰硕,初步完成逻辑方阵的体系构建。归纳起来,这个体系构建呈现三大转变:表记对象上由单一化向复合化转变、构建图式上由平面型向立体型转变、从生成方式上由逻辑形式的有限组合向无限再生转变。
一、单一化向复合化转变
波伊提乌最早构建的逻辑方阵表记对象具有明显的单一性。即表记对象只限于全称肯定命题(A)、全称否定命题(E)、特称肯定命题(I)和特称否定命题(O)两两之间的真假制约关系。之后首先开启了逻辑方阵表记对象的复合化研究。就简单命题领域,现已扩展到具有同素材的全称肯定区别命题(Aa)、全称否定区别命题(Ee)、特称肯定区别面积(Ia)和特称否定区别命题(Oa)四个区别命题(discriminate proposition)之间;必须P(Op)、必须非P(O┓p)、允许P(Pp)、允许非P(P┓p)四个直言规范命题(deontic proposition)之间;过去时段P(Ap)、过去时段非P(A┐p)、过去时点P(Hp)、过去时点非P(H┐p),将来时段P(Gp)、将来时段非P(G┐p)、将来时点P(Fp)、将来时点非P(F┐p)时态命题(chronological proposition)之间;必然肯定命题(apodeictic affirmation proposition)LP、必然否定命题(apodeictic negation proposition)L┓P、可能肯定命题(problematic affirmation proposition)MP、可能否定命题(problematic negation proposition)M┓P四个模态命题(modal proposition)之间。以上表记对象只有一个变元,构建的逻辑方阵称为简单型逻辑方阵。
逻辑方阵表记对象的复合化研究并未就此止步,先后经周钺(1984)[2],许存信(1987)[3],汪志恺(1988)[4],翟东林,孙启明(1993)[5],胡满场(1997)[6]等不断探索,将逻辑方阵表记对象扩展到复合命题领域。笔者“通过对简单命题p q、到简单复合命题再到简单复合命题推理这纵向层面的全面推演,归纳出三十九个逻辑方阵,初步完成了逻辑方阵的构建体系”[7]。将逻辑方阵表记对象扩展到复合推理领域和复合命题与复合推理交叉领域,即表记对象包含两个以上命题变元的复杂型逻辑方阵。逻辑方阵表记对象完成从单一化向复合化转变。
二、平面型向立体型转变
表记对象的数量为4个逻辑形式的逻辑方阵称为平面型逻辑方阵,构图为正方形,历史上还有“逻辑正方形”、“对当方阵”、“逻辑矩阵”、“逻辑魔方”[8]等不同名称。以上论述的表记对象上由单一化向复合化转变的全部逻辑方阵均为平面型逻辑方阵。
平面型逻辑方阵均可通过“平行移行”规则构建。[9]不管由多少命题变元构成的逻辑形式,只要其逻辑关系属于上反对关系、下反对关系或差等关系(不能是矛盾关系)中的一种关系,都可以通过“平行移行”规则构建完整的平面型逻辑方阵。原线段所属逻辑关系不同平移方向也不同,如原线段属差等关系则向左或右移动、如原线段属上反关系对则向下移动、如原线段属下反对关系则向上移动;如p∧q和┐p→┐q两逻辑形式为差等关系,两逻辑形式的矛盾关系分别为┐p∨┐q、┐p∧q。根据“平行移行”规则,将差等关系的p∧q和┐p→┐q形成的纵线段为起点,向右平行移动至┐p∧q、┐p∨┐q等距离位置,再将四个定点的另外五条线段连接起来,即构建图1平面型逻辑方阵。自然,p∧q和┐p∧q为上反对关系,┐p→┐q和┐p∨┐q为下反对关系,┐p∧q和┐p∨┐q必为差等关系。
笔者在2007年最早提出建立立体逻辑方阵的构想,认为“包含两个自变元的联言命题与相容选言命题、充分条件假言命题、必要条件假言命题,通过前肢互否、后肢互否、双肢互否和非双肢互否等方式形成的各个命题之间,仍具有真假制约关系,在此基础上提出建立立体逻辑方阵的构想。”[10]与平面逻辑方阵相比较,立体逻辑方阵表记对象增加至八个。如相容选言命题p∨q与其前肢互否命题┐p∨q、后肢互否命题p∨┐q、双肢互否命题┐p∨┐q(分别用A、B、C、D表示)与对应的否定命题┐(p∨┐q)、┐(┐p∨┐q)、┐(p∨q)、┐(┐p∨q)(分别用┐A、┐B、┐C、┐D表示)之间的真假制约关系(省略真值判断环节)可用图2立体逻辑方阵表示。图2中构成平面┐A┐B┐C┐D的线段┐A┐B、┐B┐C、┐C┐D、┐D┐A、┐A┐C、┐B┐D全为上反对关系,平面ABCD 的线段AB、BC、CD、DA、AC、BD 全为下反对关系,立体逻辑方阵的侧面线段┐AC、┐AD、┐BC、┐BD、┐BA、┐CD、┐CA、┐CB、┐DA、┐DB、┐DC、┐AB全为差等关系,立体逻辑方阵的对角线┐AA、┐BB、┐CC、┐DD全为矛盾关系。可见,立体型逻辑方阵和平面型逻辑方阵极为相似,便于识记。
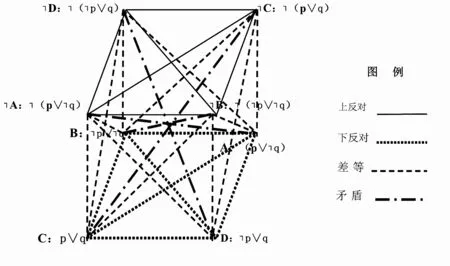
图2 立体型逻辑方阵
从表记对象看,立体型逻辑方阵和平面型逻辑方阵一样,具有复合化特征。截至目前,立体型逻辑方阵的表记对象也扩展至以下领域:第一,联言命题与相容选言命题及其异变形式(前肢互否、后肢互否、双肢互否)之间、联言命题与充分条件命题及其异变形式之间和联言命题与必要条件命题及其异变形式之间的真假制约关系;第二,复合命题(联言命题、相容选言命题、充分条件假言命题、必要条件假言命题)的异变形式及其负命题之间的真假制约关系;第三,复合推理(相容选言推理、充分条件假言推理、必要条件假言推理、二难推理)无效式的异变形式及其否定形式之间的真假制约关系,不相容选言推理和充要条件假言推理无效式及其否定形式之间的真假制约关系。这些真假制约关系均可用立体逻辑方阵表示,这都为立体逻辑方阵的建立找到了实际依据,标志逻辑方阵由平面型向立体型转变。
三、逻辑形式的有限组合向无限再生转变
就目前的研究看,逻辑方阵不管是简单型还是复杂型,不管是基本类型还是派生型,均由有限的逻辑形式组合而形成。这些逻辑形式涉及简单命题、复合命题、复合推理等有限组合,这里不赘述。
逻辑方阵绝不限于具有真假制约关系的有限的逻辑形式的组合,还是一个可无限再生的系统。
笔者在拙文《永真公式形成系统初探》[11]中根据四个命题形式之间的永真关系构建一个永真公式系统。按此系统,一个方阵本来可有八个永真公式,这些永真公式可直接等值转换的以一个计,这样一个方阵可推演出三个永真公式,14个基本类型的复合命题逻辑方阵可推演出如下四十二个永真公式:
(1)(p∧q)→(p∨q) (2)(p∨q)∨(┐p∨┐q)
(3)(┐p∨┐q)←(┐p∧┐q) (4)(p∧q)→((p∧q)∨(┐p∧┐q))
(5)((p∧q)∨(┐p∧┐q))∨(┐p∨┐q) (6)(┐p∨┐q)←(pq)
(7)(p∧q)→(p→q) (8)(p→q)∨(┐p∨┐q)
(9)(┐p∨┐q)←(p∧┐q) (10)(p∧q)→(p←q)
(11)(p←q)∨(┐p∨┐q) (12)(┐p∨┐q)←(┐p∧q)
(15)(┐p∨┐q)←((p∧┐q)∨(┐p∧q) (16)(pq)→(p∨q)
(17)(p∨q)∨((p∧q)∨(┐p∧┐q))
(18)((p∧q)∨(┐p∧┐q))←(┐p∧┐q)
(19)(p∧┐q)→(p∨q) (20)(p∨q)∨(p→q)
(21)(p→q)←(┐p∧┐q)(22) (┐p∧q)→(p∨q)
(23)(p∨q)∨(p←q) (24)(p←q)←(┐p∧┐q)
(25)((p∧┐q)∨(┐p∧q))→(p∨q) (26)(p∨q)∨(pq)
(31)(┐p∧q)→(pq) (32)(pq)∨(p←q)
(33)(p←q)←((p∧q)∨(┐p∧┐q)) (34)(┐p∧q)→(p→q)
(35)(p→q)∨(p←q) (36)(p←q)←(p∧┐q)
(39)((p∧┐q)∨(┐p∧q))←(p∧┐q) (40)(pq)→(p←q)
(41)(p←q)∨((p∧┐q)∨(┐p∧q)) (42)((p∧┐q)∨(┐p∧q))←(┐p∧q)
(一)逻辑方阵一次再生系统
如以(p∧q)+(┐p∧┐q)+(p∨q)+(┐p∨┐q)对应的逻辑方阵推演出的(1)(2)(3)三个永真公式为构建依据,可推演出9个逻辑方阵。
1.(p∧q)→(p∨q)
前肢互否:(┐p∨┐q)→(p∨q)
后肢互否:(p∧q)→(┐p∧┐q)
双肢互否:(┐p∨┐q)→(┐p∧┐q)
三个蕴涵式两两间均为下反对关系。与此三个蕴涵式相矛盾的合取式分别为:(┐p∨┐q)∧(┐p∧┐q)、(p∧q)∧(p∨q)、(┐p∨┐q)∧(p∨q)。根据“平行移行”规则推演出真假制约关系,构建如下逻辑方阵:
(Ⅰ)(p∧q)∧(p∨q) (┐p∨┐q)∧(┐p∧┐q)
(┐p∨┐q)→(p∨q) (p∧q)→(┐p∧┐q)
(Ⅱ)(┐p∨┐q)∧(p∨q) (┐p∨┐q)∧(┐p∧┐q)
(┐p∨┐q)→(p∨q) (┐p∨┐q)→(┐p∧┐q)
(Ⅲ)(┐p∨┐q)∧(p∨q) (p∧q)∧(p∨q)
(p∧q)→(┐p∧┐q) (┐p∨┐q)→(┐p∧┐q)
2.(p∨q)∨(┐p∨┐q)
前肢互否:(┐p∧┐q)∨(┐p∨┐q)
后肢互否:(p∨q)∨(p∧q)
双肢互否:(┐p∧┐q)∨(p∧q)
三个蕴涵式两两间均为下反对关系。与此三个蕴涵式相矛盾的合取式分别为:(p∨q)∧(p∧q)、(┐p∧┐q)∧(┐p∨┐q)、(p∨q)∧(┐p∨┐q)。根据“平行移行”规则推演出真假制约关系,构建如下逻辑方阵:
(Ⅳ)(┐p∧┐q)∧(┐p∨┐q) (p∨q)∧(p∧q)
(┐p∧┐q)∨(┐p∨┐q) (p∨q)∨(p∧q)
(Ⅴ)(p∨q)∧(┐p∨┐q) (p∨q)∧(p∧q)
(┐p∧┐q)∨(┐p∨┐q) (┐p∧┐q)∨(p∧q)
(Ⅵ)(p∨q)∧(┐p∨┐q) (┐p∧┐q)∧(┐p∨┐q)
(p∨q)∨(p∧q) (┐p∧┐q)∨(p∧q)
3.(┐p∨┐q)←(┐p∧┐q)
前肢互否:(p∧q)←(┐p∧┐q)
后肢互否:(┐p∨┐q)←(p∨q)
双肢互否:(p∧q)←(p∨q)
三个蕴涵式两两间均为下反对关系。与此三个蕴涵式相矛盾的合取式分别为:(┐p∨┐q)∧(┐p∧┐q)、(p∧q)∧(p∨q)、(┐p∨┐q)∧(p∨q)。根据“平行移行”规则推演出真假制约关系,构建如下逻辑方阵:
(Ⅶ).(p∧q)∧(p∨q) (┐p∨┐q)∧(┐p∧┐q)
(p∧q)←(┐p∧┐q) (┐p∨┐q)←(p∨q)
(Ⅷ).(┐p∨┐q)∧(p∨q) (┐p∨┐q)∧(┐p∧┐q)
(p∧q)←(┐p∧┐q) (p∧q)←(p∨q)
(Ⅸ).(┐p∨┐q)∧(p∨q) (p∧q)∧(p∨q)
(┐p∨┐q)←(p∨q) (p∧q)←(p∨q)
按照这种构建方式,以上42个永真公式又可再生出126个逻辑方阵。
类似地,以析取律p→(p∨q)推演出的逻辑方阵表记的p∧(p∨q)、p∧(┓p∧┓q)、┓p→(p∨q)、p→(┓p∧┓q)命题形式为例,又可派生出三个永真公式:
(p∧(p∨q))→(p∧(┓p∧┓q)) (p∧(┓p∧┓q))∨(┓p→(p∨q))
(┓p→(p∨q))←(p→(┓p∧┓q))
仍按以上的推演顺序,先将每个永真公式分别按前肢互否、后肢互否、双肢互否均派生出三个协调式。三个协调式均为下反对关系,与其矛盾式相对应,根据“平行移行”规则构建三个逻辑方阵。以上三个永真公式即能构建九个逻辑方阵:
(1)(p∧(p∨q))∧((p∧(┓p∧┓q)) (┓p∨(┓p∧┓q))∧(┓p∨(p∨q))
(┓p∨(┓p∧┓q))→(p∧(┓p∧┓q)) (p∧(p∨q))→((┓p∨(p∨q))
(2)(┓p∨(┓p∧┓q))∧((p∧(┓p∧┓q)) (┓p∨(┓p∧┓q))∧(┓p∨(p∨q))
(┓p∨(┓p∧┓q))→(p∧(┓p∧┓q)) (┓p∨(┓p∧┓q))→((┓p∨(p∨q))
(3)(┓p∨(┓p∧┓q))∧((p∧(┓p∧┓q)) (p∧(p∨q))∧((p∧(┓p∧┓q))
(p∧(p∨q))→((┓p∨(p∨q)) (┓p∨(┓p∧┓q))→((┓p∨(p∨q))
(4)(┓p∨(p∨q))∧(p∨(p∨q)) (p∧(┓p∧┓q))∧(┓p∧(┓p∧┓q))
(┓p∨(p∨q))∨(┓p→(p∨q)) (p∧(┓p∧┓q))∨(┓p∧(┓p∧┓q))
(5)(p∧(┓p∧┓q))∧(p∨(p∨q)) (p∧(┓p∧┓q))∧(┓p∧(┓p∧┓q))
(┓p∨(p∨q))∨(┓p→(p∨q)) (┓p∨(p∨q))∨(┓p∧(┓p∧┓q))
(6)(p∧(┓p∧┓q))∧(p∨(p∨q)) (┓p∨(p∨q))∧(p∨(p∨q))
(p∧(┓p∧┓q))∨(┓p∧(┓p∧┓q))(┓p∨(p∨q))∨(┓p∧(┓p∧┓q))
(7)(┓p∧(┓p∧┓q))∧(p∧(p∨q)) (p∨(p∨q))∧(p→(┓p∧┓q))
(┓p∧(┓p∧┓q))←(p→(┓p∧┓q))(┓p→(p∨q))←(p∧(p∨q))
(8)(p∨(p∨q))∧(p∧(p∨q)) (p∨(p∨q))∧(p→(┓p∧┓q))
(┓p∧(┓p∧┓q))←(p→(┓p∧┓q))(┓p∧(┓p∧┓q))←(p∧(p∨q))
(9)(p∨(p∨q))∧(p∧(p∨q)) (┓p∧(┓p∧┓q))∧(p∧(p∨q))
(┓p→(p∨q))←(p∧(p∨q)) (┓p∧(┓p∧┓q))←(p∧(p∨q))
(二)逻辑方阵二次再生系统
任何一个逻辑方阵经一次再生,可构建九个逻辑方阵。我们以如上表达式(1)作为推演的起点,进行二次再生推演,仍可构建九个逻辑方阵。
二次再生中,以逻辑方阵表记的(p∧q)∧(p∨q)、(┐p∨┐q)∧(┐p∧┐q)、(┐p∨┐q)→(p∨q)、(p∧q)→(┐p∧┐q)四命题为例,又可派生出三个永真公式:
((p∧q)∧(p∨q))→((┐p∨┐q)→(p∨q))
((┐p∨┐q)→(p∨q))∨((p∧q)→(┐p∧┐q))
((p∧q)→(┐p∧┐q))←((┐p∨┐q)∧(┐p∧┐q))
仍按以上的推演顺序,先将每个永真公式分别按前肢互否、后肢互否、双肢互否均派生出三个协调式。三个协调式均为下反对关系,与其矛盾式相对应,根据“平行移行”规则构建三个逻辑方阵。以上三个永真公式即能构建九个逻辑方阵:
(1)((┐p∨┐q)∨(┐p∧┐q))→((┐p∨┐q)→(p∨q))
((p∧q)∧(p∨q))→((┐p∨┐q)∧(┐p∧┐q))
((p∧q)∧(p∨q))∧((p∧q)∨(p∨q))
((┐p∨┐q)∨(┐p∧┐q))∧((┐p∨┐q)∧(┐p∧┐q))
(2)((┐p∨┐q)∨(┐p∧┐q))→((┐p∨┐q)→(p∨q))
((┐p∨┐q)∨(┐p∧┐q))→((┐p∨┐q)∧(┐p∧┐q))
((┐p∨┐q)∨(┐p∧┐q))∧((p∧q)∨(p∨q))
((┐p∨┐q)∨(┐p∧┐q))∧((┐p∨┐q)∧(┐p∧┐q))
(3)((p∧q)∧(p∨q))→((┐p∨┐q)∧(┐p∧┐q))
((┐p∨┐q)∨(┐p∧┐q))→((┐p∨┐q)∧(┐p∧┐q))
((┐p∨┐q)∨(┐p∧┐q))∧((p∧q)∨(p∨q))
((p∧q)∧(p∨q))∧((p∧q)∨(p∨q))
(4)((┐p∨┐q)∧(┐p∧┐q))∨((p∧q)→(┐p∧┐q))
((┐p∨┐q)→(p∨q))∨((p∧q)→(p∨q))
((┐p∨┐q)∧(┐p∧┐q))∧((p∧q)∧(┐p∧┐q))
((p∧q)∨(p∨q))∧((p∧q)∧(p∨q))
(5)((┐p∨┐q)∧(┐p∧┐q))∨((p∧q)→(┐p∧┐q))
((┐p∨┐q)∧(┐p∧┐q))∨((p∧q)→(p∨q))
((p∧q)∨(p∨q))∧((p∧q)∧(┐p∧┐q))
((p∧q)∨(p∨q))∧((p∧q)∧(p∨q))
(6)((┐p∨┐q)→(p∨q))∨((p∧q)→(p∨q))
((┐p∨┐q)∧(┐p∧┐q))∨((p∧q)→(p∨q))
((p∧q)∨(p∨q))∧((p∧q)∧(┐p∧┐q))
((┐p∨┐q)∧(┐p∧┐q))∧((p∧q)∧(┐p∧┐q))
(7)((p∧q)∧(p∨q))←((┐p∨┐q)∧(┐p∧┐q))
((p∧q)→(┐p∧┐q))←((p∧q)∨(p∨q))
((p∧q)∧(p∨q))∧((p∧q)∨(p∨q))
((┐p∨┐q)∨(┐p∧┐q))∧((┐p∨┐q)∧(┐p∧┐q))
(8)((p∧q)∧(p∨q))←((┐p∨┐q)∧(┐p∧┐q))
((p∧q)∧(p∨q))←((p∧q)∨(p∨q))
((┐p∨┐q)∨(┐p∧┐q))∧((p∧q)∨(p∨q))
((┐p∨┐q)∨(┐p∧┐q))∧((┐p∨┐q)∧(┐p∧┐q))
(9)((p∧q)→(┐p∧┐q))←((p∧q)∨(p∨q))
((p∧q)∧(p∨q))←((p∧q)∨(p∨q))
((┐p∨┐q)∨(┐p∧┐q))∧((p∧q)∨(p∨q))
((p∧q)∧(p∨q))∧((p∧q)∨(p∨q))
可见,任何一个逻辑方阵均包含三个永真公式。任何一个永真公式(包括推理形式)按前肢互否、后肢互否、双肢互否均派生出三个协调式,根据“平行移行”规则可构建三个逻辑方阵,三个永真公式即能构建九个逻辑方阵。即每一个逻辑方阵经一次再生即能构建九个逻辑方阵。
拙文《复合命题推理逻辑方阵类型研究》[12]、《逻辑方阵类型再探》[13]中认为复合命题逻辑方阵有14个基本类型和18个派生类型,复合推理逻辑方阵23个基本类型和20个派生类型。据此,以一次再生计,14个复合命题逻辑方阵基本类型可再生126个逻辑方阵,18个复合命题逻辑方阵派生类型可再生162个逻辑方阵,23个复合推理逻辑方阵基本类型可再生207个逻辑方阵,20个复合推理逻辑方阵派生类型可再生180个逻辑方阵(见表1)。按此构建系统,逻辑方阵还可二次再生,直至无限再生,自然逻辑方阵的表记对象也是一个无限再生系统。
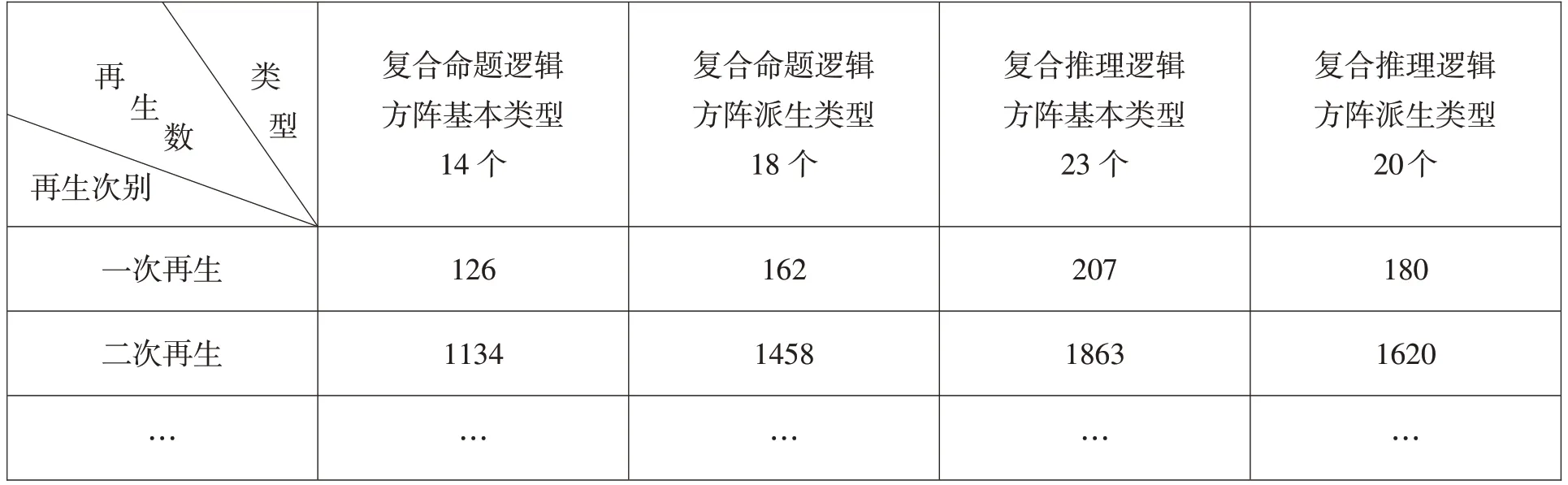
表1 逻辑方阵的无限再生系统
至此,学界初步完成了逻辑方阵的构建体系。这个构建体系实现了表记对象上由单一化向复合化转变,构建图式上由平面型向立体型转变,从生成方式上由逻辑形式的有限组合向无限再生转变。从根本上看,把逻辑方阵的表记对象拓展到无限领域,揭示逻辑方阵的表记对象再生机制:逻辑方阵是一个可无限再生系统,以便更好地反映逻辑方阵理论的全貌。
逻辑方阵的构建体系的三大转变将逻辑方阵的表记对象拓展到无限领域,使逻辑方阵具有真正意义上的普遍适用性。三次转变分别实现了逻辑方阵表记对象、构建图式、生成方式上的创新,据此进一步推演出无限再生的庞大的逻辑方阵体系。由无限再生的逻辑方阵推演出来的永真式、矛盾式和协调式也是一个无限再生系统,大大拓展了逻辑学的理论和应用研究空间,对促进逻辑学的未来发展产生重要影响。

