例析构建圆的模型巧解向量最值问题

胡弋芳

江西师范大学数学与统计学院 (330022)

向量最值是高中数学很常见问题，根据相关代数条件构造几何图形，从其特征、性质入手巧解向量问题是一种较为简便的方法.其中圆是数学中重要的几何图形，其在解决此类问题时易被忽视，特别是需要根据问题的描述，寻找“隐圆”，建立圆的模型来求解，往往是一种“妙招”本文通过具体的例题来分析说明.

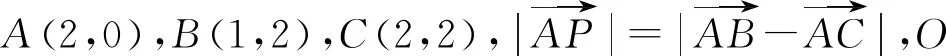
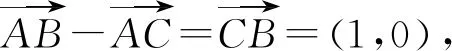
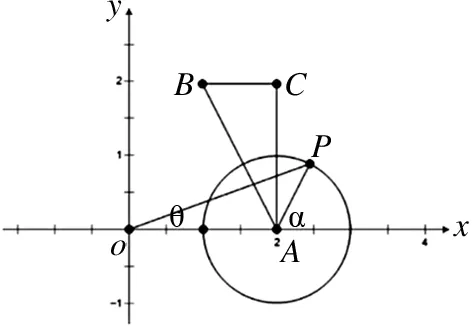
图1

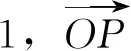
点评：本题也可设点P坐标为(x,y)，然后根据夹角公式列出相应式子，但在化简时学生可能会有点困难，导致无法求出夹角最大值.而向量模长为定值意味着点P与点A之间的距离是固定不变的，这符合圆的定义，所以构建圆模型直接从图形中就可看出夹角最大值在何处取得，简单又快速.

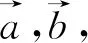
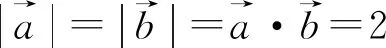
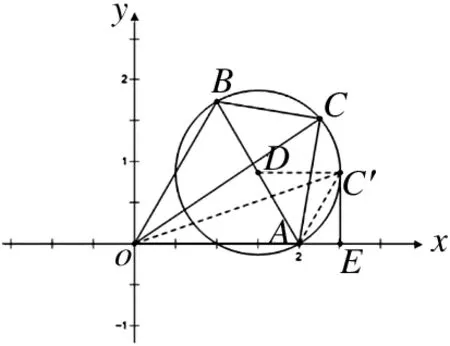
图2

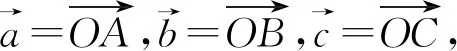
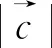
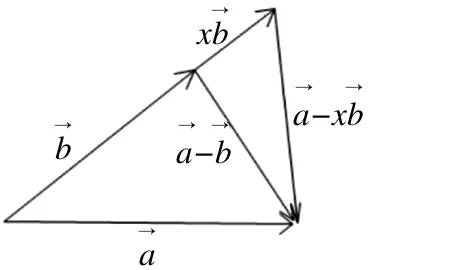
图3

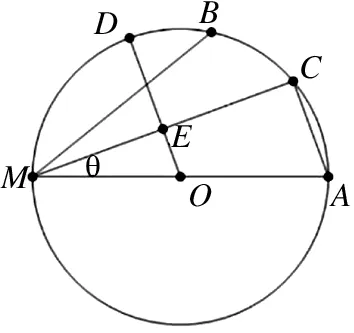
图4

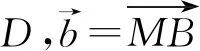
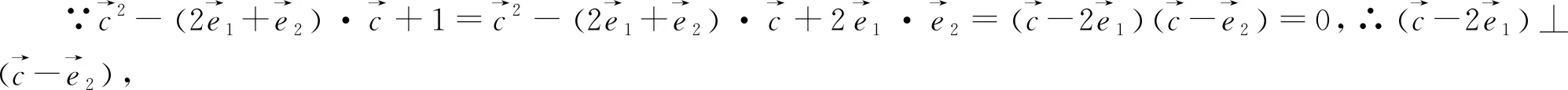
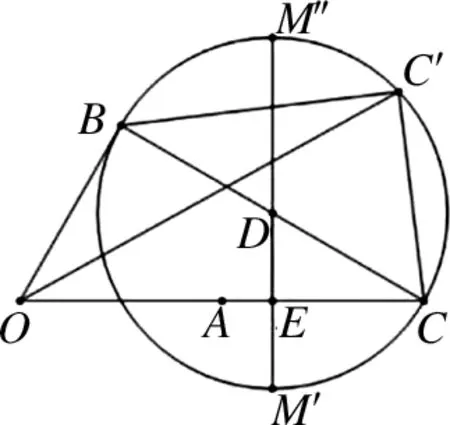
图5

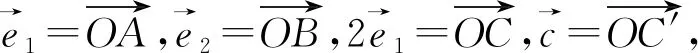
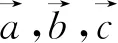
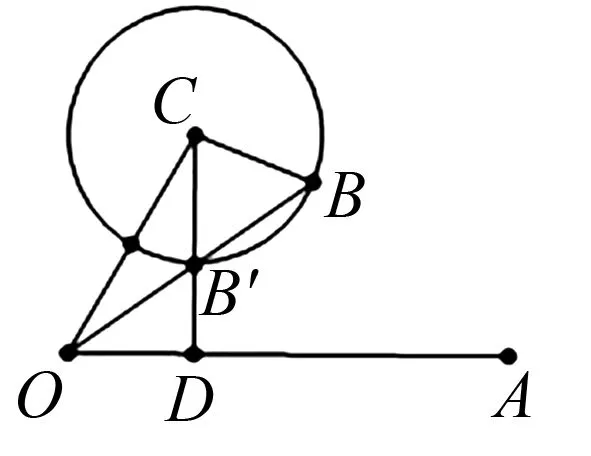
图6

点评：因式分解和完全平方是个难点，有时条件不是很明显，这时就需要将方程中的某些量进行转化或先进行化简，然后根据具体题目选择合适方式.这类题型给出的已知条件都很少，用代数方法求解都会比较困难，所以结合图形求解是最好的方法.而由因式分解或完全平方得出的隐含信息要么符合圆的定义，要么是圆性质的体现，这无疑表明可构建圆模型来求解，既直观又易理解.

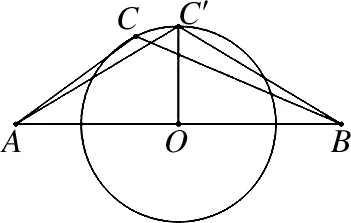
图7

分析：由极化恒等式和数量积为定值知点C在以AB中点为圆心，半径长为r=

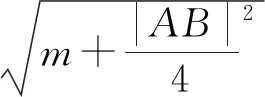
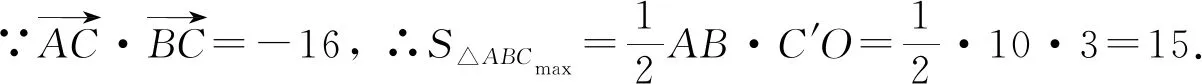
点评：数量积是一定值(不为零)也可以构建圆来求解，利用平面向量的极化恒等式可将其转化为向量模长为一定值的问题，进而根据圆的定义构建圆.本题较容易，通过设坐标的方法也能求解，只是数形结合的方法更快，只需带入公式即可.

向量的问题灵活多变，求解向量的方法也多种多样.而对于计算较复杂或具有某些较明显特征的向量问题，往往可试着找出“隐圆”来简便计算.运用这种数形结合的方式，使得问题变得更为直观，更易理解.既快速解决了问题，也间接地培养了数学建模素养.