基于隐Markov模型的广义Markov跳变系统的控制器设计

赵俊杰, 李 博, 杜友武

(江苏理工学院, 江苏 常州 213001)

在航空、电力、经济、制造、网络等实际工程领域中,由于各种因素的存在,导致其建立的数学模型的结构以及参数发生突发性改变,而Markov 跳变系统是一类受到Markov 链约束的混杂系统,可用于描述上述系统。 基于此,学术界产生了诸多关于Markov跳变系统的创新性成果。值得注意的是,广义系统能够更好地描述上述系统,所得结果应用范围更加广泛,因此针对广义Markov跳变系统的研究成为一个热点。由于广义系统矩阵的存在,必须同时考虑系统的正则性以及无脉冲性,以确保问题有解以及解的唯一性,这使得广义系统的研究更为复杂[1]66,[2]14。另一方面,信息的传输往往存在一定的延迟,这使得考虑时滞Markov系统的控制问题变得十分必要[3-5]。在很多实际系统中,由于物理结构等因素的限制,控制量往往有一定的限制,这就导致了执行器的饱和,从而带来非线性问题,使得问题的处理更加复杂。文献[6]针对一类离散Markov跳变系统,考虑执行器饱和存在的情况,设计了H∞控制器,使得闭环系统随机稳定并具备一定的抗干扰能力[6]。

针对Markov跳变系统的研究成果较为充分,但值得注意的是,由于网络延时导致通信失败,使得控制器模态与系统模态不能保持一致,因此在这种情况下,考虑隐Markov系统的相关控制问题十分必要。[7],[8]4024。但实际系统中往往会出现时滞、输入饱和、转移概率不完全已知等情况,因此,围绕该问题,继续进行深入研究具有重要的意义。

综上所述,本文针对一类广义Markov跳变时滞系统,考虑输入饱和、转移概率部分未知、切换点状态不连续等实际因素,完成状态反馈控制器的设计,所得控制器能够保证闭环系统均方意义下的指数稳定性。

1 数学模型及预备知识

设计广义Markov跳变系统数学模型如下:

sat(u(t))x(j)=η(j),j∈[-max(h,τ(t)),0]

(1)

其中x(t)∈Rn为状态变量,u(t)∈Rm为控制输入,η(j)为系统初始状态函数。分布时滞h为已知常量,时变时滞项τ(t)满足下列条件:

(2)

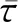
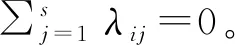
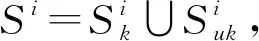
为后续推导方便,对任意r(t)=i∈S,本文定义Ai=A(r(t)),其它系统矩阵作类似定义。

sat(u(t))为输入饱和,限制条件如下:

-u0i≤sat(ui)≤u0i,u0i>0

(3)

本文基于隐Markov模型设计如下状态反馈控制器:

u(t)=kσ(t)x(t)

(4)

其中kσ(t)∈Rm×n,其跳变概率满足:

将控制器(4)代入系统(1),可得:

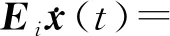
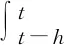
(5)

其中ψ(u(t))=sat(u(t))-u(t)。

考虑到Ei为奇异矩阵,这里存在非奇异矩阵Mi,Ni,使得:

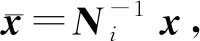
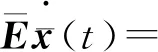
(6)

其中:

主要结果之前首先给出如下定义及引理。

定义1[1]67:正则性与无脉冲

称系统(6)为正则的,如果对任意i∈S,有:

称系统(6)为无脉冲的,如果对任意i∈S,有:

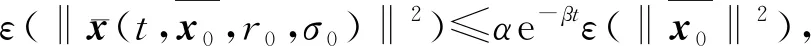
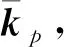
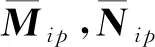
那么系统(6)等价于如下系统:

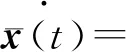
(7)

其中:

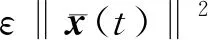
2 主要结果

(8)

(9)

(10)

(11)

(12)

(13)

(14)

其中:

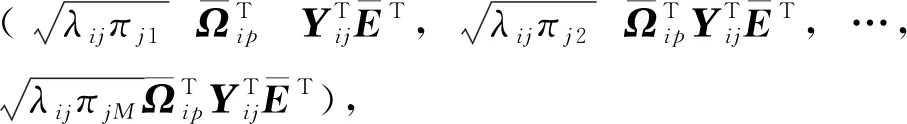
Φip=(Φi1p,Φi2p,…,ΦiNp),

以及

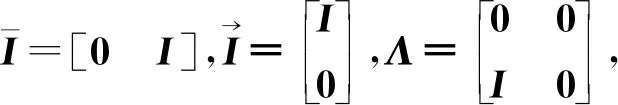
证明:对任意r(t)=i∈S,选取如下Lyapuonv-Krasovkii函数:

(15)

令r(t)=i,σ(t)=p,可得

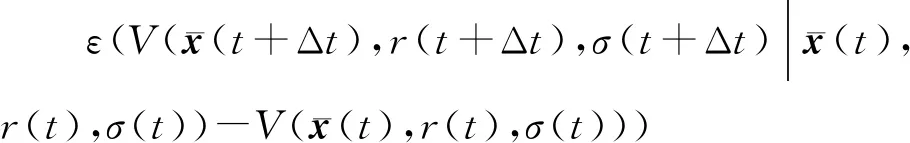
(16)

当i=j时,由系统(6)易得:

将上式代入式(16)第二行可得:

(17)

若i≠j,则此时需要考虑切换点前后状态不一致的问题,由系统(7)可得:

(18)

将式(18)代入(16)第一行可得:

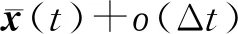
(19)

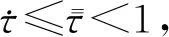
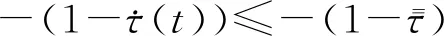
考虑引理1,进一步可得:

将上述两式代入式(16)的第二第三行,结合式(17)、(19)可得:

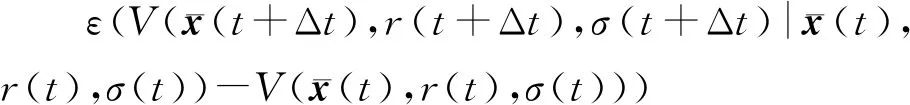
(20)

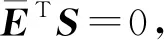
(21)

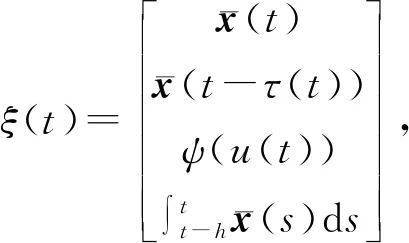
+ξ(t)TOipξ(t)

(22)

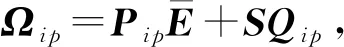
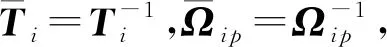
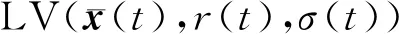
(23)

其中:

构造如下矩阵:

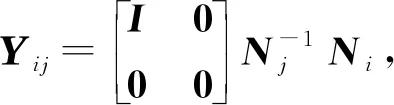
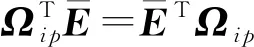
构造如下矩阵:

对定理1中不等式(8)左乘右乘该矩阵及其转置可得:

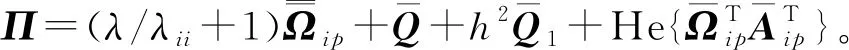
利用Schur补引理可得:

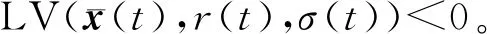
令:

δ5=λmax(Q1),

易得:

(24)

另一方面由V函数的结构可以得到:

(25)

由Dynkin引理进一步可得:

(26)

通过伊藤公式可知:

由上述不等式可以得到:

由定义2可知,系统(6)为均方意义下的指数稳定。由条件(11)—(14)并利用Schur补引理可以得到:

(27)

下面证明系统(6)是正则及无脉冲的。令:

由条件(8)可得:

(28)

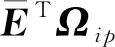
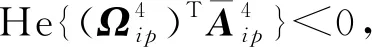
定理2:对任意r(k)=i∈S,考虑转移概率部分未知,如果存在模态相关矩阵Wi,使得条件(10)—(14)以及下列式子成立:

(29)

(30)

(31)

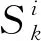
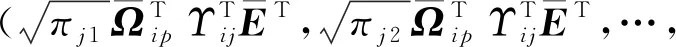
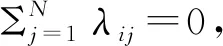
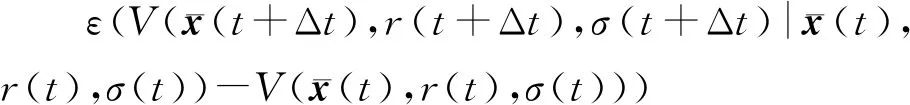
(32)

可将式(32)分为转移概率已知及未知部分,其中已知部分如下:

(33)

未知部分如下:

(34)

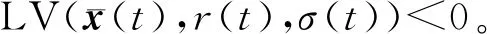
后续证明过程与定理1证明过程类似,此处不再赘述。

证明完毕。

3 数值算例

考虑具有下列系数矩阵的时滞广义Markov系统:

选择

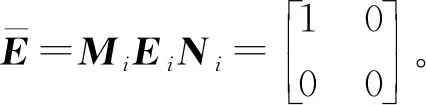
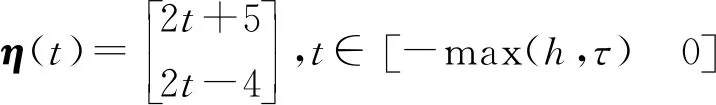
转移概率矩阵如下所示:

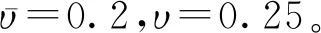
通过Matlab中Simulink工具箱搭建系统,代入系统模型参数以及上述控制器参数得到仿真图像如图1—图3,其中图1、图2分别为系统模态跳变以及控制器模态跳变曲线,图3为闭环系统状态响应曲线,由图可知本文设计的状态反馈控制器能够保证闭环系统为均方意义下指数稳定。

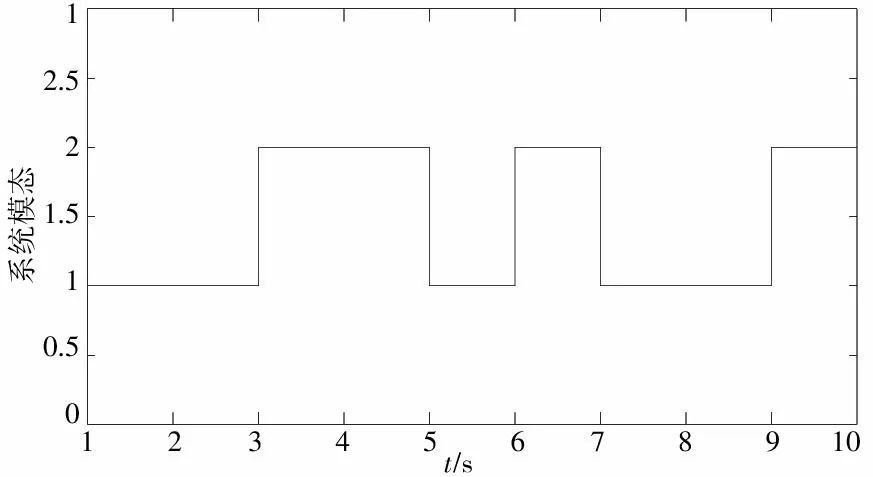
图1 系统模态跳变曲线

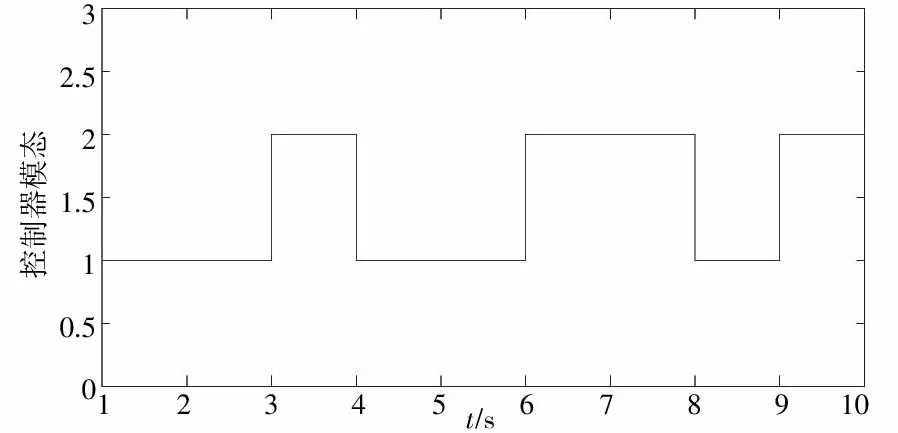
图2 控制器模态跳变曲线

图3 闭环系统状态响应曲线

4 结语

针对一类广义Markov跳变系统,考虑时变时滞、输入饱和等情况,从微分的基本方法入手,进一步考虑切换点前后状态不一致的问题,并设计状态反馈控制器,保证闭环系统是均方意义下指数稳定的,并进一步考虑转移概率部分未知的情况,给出了问题有解的充分条件以及控制器的设计方法。