一道解析几何动点轨迹方程问题的变式与推广

华南师范大学数学科学学院(510631) 李崇榆 蒋旺旺

1 试题呈现与解答

题目(2023 届广州高三零模卷第21 题) 已知抛物线C:y2=2px(p>0)的焦点F到准线的距离为2,圆M与y轴相切,且圆心M与抛物线C的焦点重合.

(1)求抛物线C和圆M的方程;

(2)设P(x0,y0)(x0̸=2)为圆M外一点,过点P作圆M的两条切线,分别交抛物线C于两个不同的点A(x1,y1),B(x2,y2)和点Q(x3,y3),R(x4,y4).且y1y2y3y4=16,证明: 点P在一条定曲线上.

该题是以直线与抛物线和圆的位置关系为命题背景,求解动点的轨迹方程问题.动点的轨迹方程问题是解析几何的重要知识点,也是高考数学中的常见题型.

解答第(1)问考查抛物线和圆的基本求法,易得抛物线C:y2=4x,圆M:(x−1)2+y2=1.

第(2)问思路一点P在一条定曲线上等价于点P关于x0,y0的轨迹方程无参数.那么如何消去参数得到P的轨迹方程呢? 观察等式y1y2y3y4=16,y1y2和y3y4可通过分别联立切线AB和切线QR与抛物线C的方程得到.那么怎么设切线的方程? 根据题意可知,切线的斜率存在且不为0,可设其方程为y−y0=k(x−x0)或x=m(y−y0)+x0.

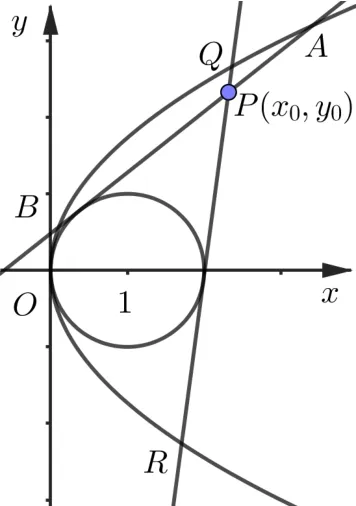
图1

若设切线AB和切线QR的斜率分别为k1,k2,利用韦达定理可用x0,y0,k1,k2表示

那么下一步只需消去k1+k2,k1k2可得关于x0,y0的方程.注意到,利用直线与圆相切的性质可列出关于k的一元二次方程,根据韦达定理可用x0,y0表示k1+k2,k1k2,代入即可求证.

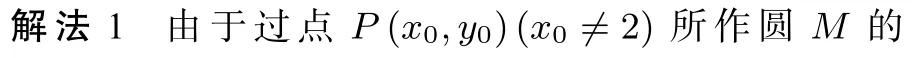
通过消元可获得关于y1y2的一元二次方程方程.类似地,由于直线CD与直线AB有相同的位置关系,即“形似”,则可以得到关于y3y4的同构方程,进而使用韦达定理表示y1y2·y3y4.这使用了”同构法”.

解法2由于过点P(x0,y0)(x0̸=2)所作圆M的两条切线,分别交抛物线C于两个不同的点,则x0̸=0,y0̸=±1,则切线斜率存在且不为0,设直线

即直线AB: 4x−(y1+y2)y+y1y2=0.由于直线AB过点P且与圆M相切,则在 ②中消去y1+y2,整理得:(y20−1)(y1y2)2+8(y20−x0)y1y2−16x20=0.同理,由于直线QR与直线AB具有相同的特征,则(y20−1)(y3y4)2+8(y02−x0)y3y4−16x20=0.因此y1y2,y3y4为关于x的一元二次方程(y02−1)x2+8(y02−x0)x−16x20=0 的两个实根,则y1y2y3y4=(y1y2)(y3y4)==16,即x20+y20=1.所以点P在圆x2+y2=1 上.

评注2在解法2 中,利用直线CD与直线AB的“形似”——过定点P且与圆M相切,得到关于y1y2和y3y4的一元二次方程是思路二的关键! 对比通法,同构法未引入新“元”,而是对整体y1+y2,y1y2或y3+y4,y3y4进行操作,不仅大大地减少了运算量,也彰显了思维的整体性与灵活性.在解析几何问题中,常有一些点、线具有相同的特征,如二次曲线上的两个点在同一条直线上、两个点在同一条二次曲线上、两条直线与二次曲线有相同位置关系、两条直线过同一个点,将这些“形”的共性坐标化,得到的代数式结构也相同,这也为“同构法”的使用提供了可能[1].

2 试题追溯与变式推广

追根溯源,与这道模拟题类似的高考题曾出现在2012年高考湖南卷(理科)第21 题中.

溯源(2012 年高考湖南卷(理科)第21 题)在直角坐标系xOy中,曲线C1上的点均在C2: (x−5)2+y2=9 外,且对C1上任意一点M,M到直线x=−2 的距离等于该点与圆C2上的点的距离的最小值.

(1)求曲线C1的方程;

(2)设P(x0,y0)(y0̸=±3)为圆C2外一点,过点P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D,

证明: 当P在直线x=−4 上运动时,四点A,B,C,D的纵坐标之积为定值.

答案(1)曲线C1:y2=20x.(2)当P在直线x=−4上运动时,四点A,B,C,D的纵坐标之积为定值6400.细节从略.

追寻动态变化中的不变一直是解析几何的研究热点.从这两道题我们可以提出一些疑问: 若将抛物线一般化为C1:y2=2px(p>0),将圆一般化为C2: (x−)2+y2=r2(r >0),设P(x0,y0)(y0̸=±r)为圆C2外一点,过点P作圆C2的两条切线,分别与抛物线C1相交于两个不同的点A(x1,y1),B(x2,y2)和C(x3,y3),D(x4,y4).任给一实数q,若y1y2y3y4=q时,P(x0,y0)是否在定曲线上? 若在,曲线的方程是什么? 这两个条件是否等价?

2)切线AB和切线CD的斜率都存在

由于A,B,C,D在抛物线C1:y2=2px上,故直线

即2px−(y1+y2)y+y1y2=0.由于直线AB过点P且与圆M相切,则

消去y1+y2,整理得:

同理,由于直线CD与直线AB具有相同的特征,则

因此,y1y2与y3y4是关于x的一元二次方程

的两个根,则∆≥0⇔(x−)2+y2−r2≥0,

即4p2r2x20+(q+4p2r2−p4)y20=r2q.由此,我们得到以下结论:

命题1已知抛物线C1:y2=2px(p>0),圆C2: (x−)2+y2=r2(r >0).设P(x0,y0)(y0̸=±r)为圆C2外一点,过点P作圆C2的两条切线,分别与抛物线C1相交于两个不同的点A(x1,y1),B(x2,y2)和C(x3,y3),D(x4,y4).任给一实数q,若曲线方程有解且曲线不在C2内,则y1y2y3y4=q⇔点P在定曲线上且曲线方程为4p2r2x2+(q+4p2r2−p4)y2=r2q.

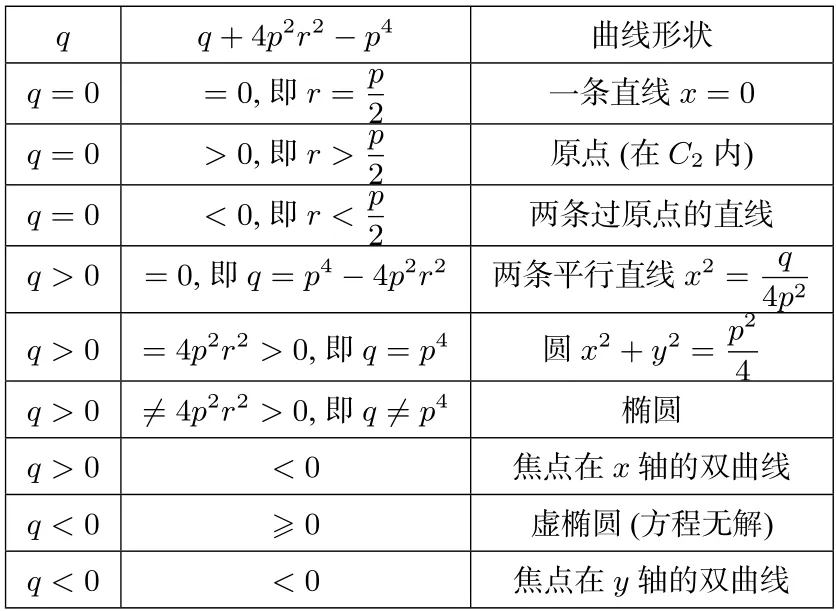
表1 当y1y2y3y4=q 时定值q 与曲线的关系

评注3由命题1 知,2023 届广州市零模第21 题中第(2)问的条件“x0̸=2”的有无不影响结论,但作为解析几何试题,其避免了对切线斜率不存在的讨论,降低了题目的难度.

我们还可以类比上述推广过程进行如下变式探究:

探究1 保持命题1 中其他条件不变,将条件y1y2y3y4=q改为y1y2+y3y4=q.

1)切线AB或切线CD的斜率不存在的情形:

命题2保持命题1 中其他条件不变,则y1y2+y3y4=q⇔点P在定曲线上且曲线方程为(q+2p2)y2=4pr2x+qr2.

表2 当y1y2+y3y4=q 时定值q 与曲线的关系

探究2 保持命题1 中其他条件不变,将条件y1y2y3y4=q改为(y1+y2)(y3+y4)=q”或“y1+y2+y3+y4=q.

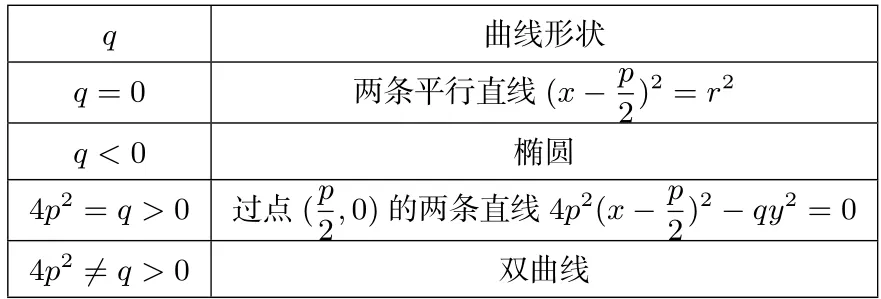
表3 当y1+y2+y3+y4=q 时定值q 与曲线的关系

命题4保持命题1 中其他条件不变,则y1+y2+y3+y4=q⇔点P在定曲线上且曲线方程为

观察到式⑦含有交叉项x0y0,仅通过平移是无法消去的.在高等数学中,二次曲线方程中的交叉项总可以通过转轴变换消去(在平面直角坐标系中,不改变原点的位置和坐标轴的长度单位,将两坐标轴按同一方向绕原点旋转同一角度的坐标变换叫做坐标轴的旋转,简称转轴).下面,我们引入高等数学知识,了解消去交叉项的方法并判断命题4 中曲线的形状,相关细节可参见[2].

引理1 (转轴公式)设坐标轴的旋转角为θ,P是平面的任意一点,在原坐标系xOy的坐标为(x,y),在新坐标系x′Oy′的坐标为(x′,y′),则

叫做坐标轴的旋转公式,简称转轴公式.

引理2 在二次曲线方程

来判定S为何种曲线的条件是:

I1I3<0椭圆I2 >0 I3=0点I1I3 >0虚椭圆I2<0 I3 ̸=0双曲线I3=0相交直线I3 ̸=0抛物线I2=0 I3=0,K1<0平行直线I3=0,K1=0重合直线I3=0,K1 >0 虚平行直线

表4 当y1y2+y3y4=q 时定值q 与曲线的关系

评注4经验证,若保持命题1 中其他条件不变,将条件“y1y2y3y4=q”改为“y1+y2+y3y4=q”或“(y1+y2)y3y4=q”,点P轨迹不能类似得到上述结论.将命题1 中的圆C2一般化为(x−a)2+(y−b)2=r2,还可以得到以下更加一般的命题:

命题5已知抛物线C1:y2=2px(p>0),圆C2:(x−a)2+(y−b)2=r2(r >0),设点P(x0,y0)(y0̸=b±r)为圆C2外一点,过点P作圆C2的两条切线,分别与抛物线C1相交于两个不同的点A(x1,y1),B(x2,y2)和C(x3,y3),D(x4,y4).任给一实数q,若曲线方程有解且曲线不在C2内,则

(1)y1y2y3y4=q⇔点P在定曲线上且曲线方程为

4p2(b2−r2)x2−8p2abxy

+[4p2(a2−r2)−q]y2+2qby+q(r2−b2)=0.

(2)y1y2+y3y4=q⇔点P在定曲线上且曲线方程为

(4pa+q)y2−4pbxy+4p(b2−r2)x

−2b(2pa+q)y+q(b2−r2)=0.

(3)y1+y2+y3+y4=q⇔点P在定曲线上且曲线方程为

qy2−4pxy+4pbx+2(2pa−qb)y+q(b2−r2)−4pab=0.

(4)(y1+y2)(y3+y4)=q⇔点P在定曲线上且曲线方程为

4p2x2−qy2−8p2ax+2qby+4p2(a2−r2)+q(r2−b2)=0.

4 命制新试题

试题设P(x0,y0)(x0̸=1 或3)为圆C2: (x−2)2+y2=1 外一点,过点P作圆C2的两条切线,分别与曲线C1:y2=8x相交于点A(x1,y1),B(x2,y2)和C(x3,y3),D(x4,y4).在①y1y2y3y4=400,②y1y2+y3y4=32,③(y1+y2)(y3+y4)=64,④y1+y2+y3+y4=0,这四个条件中选一个作为已知条件,证明: 点P在定曲线上.

解由题意知,p=4,r=1.若选条件1,则由命题1 知点P在椭圆4x2+13y2=25 上.若选条件2,则由命题2 知点P在抛物线y2=上.若选条件3,则由命题3 知点P在过点(2,0)的两条直线(x−2)2−y2=0 上.若选条件4,则由命题4 知点P在过点(2,0)的两条直线y=0 或x=2 上.