空间圆形物体的共形几何代数拟合方法

焦卫东,庞艳丽

(中国民航大学天津市智能信号与图像处理重点实验室,天津 300300)

1 引言

城市地铁施工中盾构技术[1]、隧道测量[2]、交通工具风洞实验以及某些圆形工业器件[3]-[6]在安装校验过程中需要按照规定的精度标准进行规范合理的安装,同时各个仪器设备在运转过程中也需要进行规范的测量。所有测量都是对空间圆形物体进行处理,而施工过程可能会给圆形器件带来不同程度的变形导致其各项参数与设计值不完全一致,且空间圆形或孔型物体的特征量无法直接进行测量,间接方法成为此类问题的首选,目前常用的方法为通过专门的测绘仪器如全站仪或三维激光扫描技术[7]采集空间圆形物体周围点集,并对采集到的坐标点利用不同的检测或拟合方法计算得到该空间圆形的特征量。

平面圆已经有了较成熟的检测方法如Hough变换[8]等,而升维变换增加了空间圆拟合的难度。目前,欧氏空间常用的空间圆检测方法主要有立体视觉方法、最小二乘拟合法[9]、改进的最小二乘拟合法。其中,文献[10]中提到的立体视觉方法,首先利用Canny算子提取圆边缘点[11],然后提取出投影椭圆中心,利用双目视觉原理得到空间圆的几何参数,由于透视投影变换时会导致空间圆中心的投影与投影椭圆的中心不一致,因此立体视觉方法在处理大型圆形物体时得到的空间圆心坐标精度不高。针对此问题,文献[12]对此进行改进,利用相机光心与成像椭圆构建空间圆锥方程,进而得到圆锥正底面从而求解出空间圆的平行平面方程,然后利用实际半径找到正确空间圆方程。该方法虽然提高了检测精度,但前提是实际半径已知,另外由于欧氏空间线性方程求解的过程繁琐,算法效率比较低。而最小二乘拟合法多是基于空间球面数学模型和平面方程进行数据处理,文献[13]中,首先将三维坐标转换到平面内进行平面圆拟合,将结果映射回三维坐标系从而得到空间圆的几何参数,该方法需要进行二维、三维坐标的转换,原理复杂且直接将三维坐标映射到平面内进行平面圆拟合误差较大。针对此问题很多学者提出了多种解决方法,主要分为两类,第一类充分结合空间圆的几何特性,即空间圆中任意两条弦对应的中垂面与空间圆所处的平面相交且交点即为平面圆的圆心,然后结合最小二乘拟合法推导出圆心计算方程,进而得到圆半径[14]。通过该方法计算得到的参数误差比较小,但依然难以避免由于欧氏空间计算的坐标相关性、多维不统一性导致的计算结构复杂、动态计算困难等问题。第二类利用奇异值(Singular Value Decomposition,SVD)分解[15]和最小二乘法进行最佳圆拟合,首先使用SVD找到最适合均值中心点集的平面,然后将均值中心点投影到拟合平面上,利用最小二乘法计算圆参数,最后将圆心换为三维坐标。该方法通过SVD的方式,求解得到适合对三维点集拟合的平面,克服了维度变换所带来的精确度不高的问题,但同时增加了算法复杂度。

上述方法在保证检测精度的前提下无法兼顾算法效率问题,而几何代数(Geometric Algebra,GA)[16][17]对几何实体独特的表示方法以及坐标不相关性的特点可以简化计算复杂度,其基本算子如内积(inner product)、外积(outer product)、几何积(geometric product),简化了几何实体在传统欧氏空间复杂坐标的表达,另外用内积替代距离等复杂的欧氏空间变量,便于高维空间到低维空间的相互转化[18][19]。2010年白志鹏、李茂宽等提出基于共形几何代数(Conformal Geometric Algebra,CGA)的平面圆拟合方法[20],在CGA空间直接表示平面圆方程,进而通过内积算子判断点与圆的关系确定最佳拟合圆。而空间圆不能在共形空间中直接表示,所以平面圆拟合的共形几何方法不再适用于空间圆拟合问题。

因此,本文在以上大量研究的基础之上,综合各自方法的优缺点,提出一种基于CGA的空间圆拟合方法。该方法在基于CGA平面圆拟合的基础上,把空间圆拟合问题的实体对象转换为球,利用CGA空间对球的中独特表示形式,把平面圆拟合转换为基于CGA的球拟合问题。进一步对求解得到的两个最佳拟合超球面,在CGA空间利用Meet算子计算两个超球面的交,结果即为最佳拟合空间圆。

2 共形几何代数

2.1 基本定义

CGA有三个基本算子,分别是内积、外积和几何积

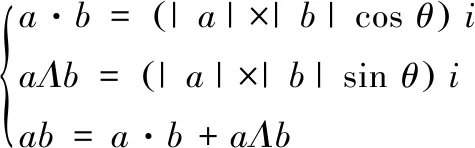
(1)

其中,a、b为向量,θ是它们之间的夹角,i表示运算空间。内积既适用于相同维度的几何对象,也可作用于不同维度的几何对象,实质上是一种降维运算,可用于求解距离和角度等标量。外积适用于任意维度的空间,通过外积可进行空间维度的扩展与几何形体的构建,实质上是一种升维运算。几何积将外积和内积结合起来,实现矢量和标量的混合维度运算,成为几何代数的核心运算,简化算法结构,提高传统代数计算的通用性。

共形几何代数相对欧氏空间又增加两个维度,空间变换从3维扩展到5维,其正交矢量基为:e1,e2,e3,e+,e-,满足

(2)

引入Rn空间无穷远点和原点

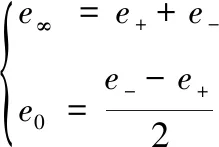
(3)

则5维共形空间的基变为:e1,e2,e3,e∞,e0。

几何实体在CGA空间可以用内积和外积两种不同的形式[21][22],表1是基本几何实体的CGA表示以及在欧氏空间中对应的表达。

表1 共形几何代数中实体的表示

2.2 基本运算

2.2.1CGA空间Meet运算

Meet运算符以统一的方式确定两个对象之间的相交关系。blade是CGA的基本元素,给定任意两个bladeA和B,如果满足

(4)

则Meet运算表达式为

M=A∩B=(B·IAB)·A=Β*·A

(5)

其中,IAB表示包括A、B的最小子空间的伪标量。判断不同对象之间的包含关系需要采用不同的相交判断算法,通过不同几何实体之间的Meet计算结果,可以生成所需的对象。本文主要讨论相交球体之间的Meet运算结果,如表2所示。

2.2.2CGA空间距离计算

CGA空间中点、圆、球可以用矢量形式表示,这些对象的内积产生标量,可以用作距离的度量。CGA空间矢量(几何实体)可以表示为

S=s1e1+s2e2+s3e3+s4e0+s5e∞s+s4e0+s5e∞

(6)

矢量P和S的内积表示为

P·S=(p+p4e∞+p5e0)·

(s+s4e∞+s5e0)=p·s-p4s5-p5s4

(7)

当P、S表示为两个点时,由表1

(8)

因此,由式(7),这两点内积为

(9)

当P表示点,S表示球时,由表1

(10)

根据式(7)得,点与球之间的内积为

(11)

此时,点与球内积的2倍等价于球半径平方减去点到球心距离的平方,内积仍然与实体间的距离有关。

另外,CGA空间中不同实体之间的内积形式各不相同,但其意义均与距离有关。

3 基于CGA的空间圆拟合

3.1 拟合模型

在欧氏空间中,求解一组点 的最优拟合球(圆),可通过求解

(12)

3.创新服务方式，推行风险提示。待条件成熟后，以“互联网+税务”和大数据应用为依托，在纳税人通过互联网正式进行年度纳税申报前，利用税务登记信息、纳税申报信息、财务会计信息、备案资料信息、第三方涉税信息等内在规律和联系，对税款计算的逻辑性、申报数据的合理性、税收与财务指标关联性等提供风险提示服务，帮助纳税人正确理解税收政策，减少纳税风险。

(13)

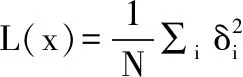
(14)

对此代价函数求解,使得代价函数最小的解即是所求的最佳拟合球。

对求得的最小非负特征解S1,S2,即分别对应最佳拟合超球和第二最佳拟合超球。从而拟合的圆为:

circle=M(S1,S2)=S1∩S2

(15)

经过计算两个最小特征解的求交,即可得到空间拟合圆方程及参数,无需进行迭代求解,因此可降低欧氏空间直接求解式(12)的计算复杂度。

3.2 算法步骤

基于CGA的空间圆拟合算法,无需通过迭代逼近的方法求其最优解,可以由式(14)及式(15)得到其解析解,理论上可以得到空间圆准确的拟合结果。其主要步骤为(流程图如图1所示):

1)获取实验数据点集{pi},并将其映射到CGA空间的数据点集{Pi};

2)利用式(13)、(14)对数据点集{Pi}求两个最小非负特征解分别对应最优拟合超球S1和第二最优拟合超球S2,从而实现CGA空间球拟合过程;

3)利用式(15),通过CGA空间Meet算子(交运算)得到目标空间圆,输出空间圆方程及相关参数;

4)利用步骤3)得到的空间圆方程及参数进行可视化表示。

4 实验分析

实验环境为Intelcorei7、2.90GHz处理器、8GB内存、Windows10 64bit计算机、python3.8平台。实验中的内积、外积、几何积、Meet算子由Gaigen系统的Clifford模块提供。实验分两组进行,第一组实验对自造三维数据集利用本文算法进行空间圆拟合,第二组实验分别对两组利用全站仪测得的某圆形钢结构参数进行空间圆拟合,并对算法的有效性进行了评估。

4.1 拟合模型

本组实验针对离散分布的三维数据点集,将本文算法(简记为CGA方法)与文献[14]中最小二乘方法(Leastsquares,Leastsq)、以及文献[15]中基于SVD的最小二乘方法(简记为SVD)进行比较。

随机生成绕圆心为(3,3,4),半径2.5的空间圆分布的100个离散数据点,实验数据点的分布如图2所示。在图2(a)表示实验数据点中几乎不存在噪声点即理想情况下,对其添加一定噪声的实验数据点如图2(b)所示。噪声点占比0.01的实验拟合结果如图3所示,CGA空间圆拟合算法通过最佳拟合超球与第二最佳拟合超球的Meet运算得到空间圆,其中图3(a)表示CGA拟合圆的球面表示,其中两个超球面的相交圆即为最佳拟合空间圆,在图3(b)中对其进行了单独表示。同样噪声点占比0.1的实验拟合结果如图4所示,图4(a)表示CGA拟合圆的球面表示,其中两个超球面的相交圆即为最佳拟合空间圆,在图4(b)中对其进行了单独表示。

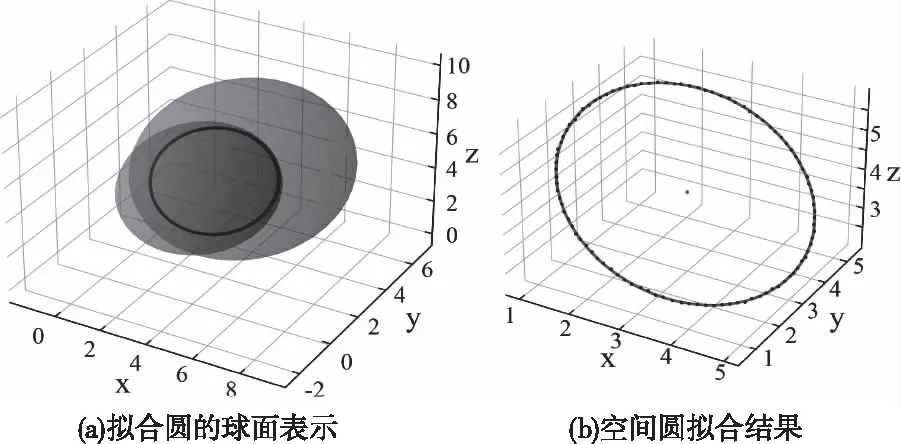
图3 噪声比占比0.01情况下CGA拟合结果

图4 噪声比占比0.1情况下CGA拟合结果

通过图3(a)、图4(a)可以看出,由于CGA空间对几何实体独特的表示方法,对空间圆拟合问题提出了新思路,即通过内积、外积算子将欧氏空间代价函数求解问题转换到CGA空间表示,避免了欧氏空间算法由于迭代次数多导致计算复杂度高、效率低的问题。无论是无噪声还是有噪声情况,CGA拟合的精度都非常高。

为进一步验证本文算法的有效性,从算法运行效率上与欧氏空间中的两种拟合方法:文献[14]中最小二乘法、文献[15]中基于SVD方法进行对比分析,结果如表3所示。

表3 检测结果及运行时间

由表3结果得到,在可靠性方面,三种算法与理论值相差不大。而基于CGA的方法相比其它两种方法具有明显的优势:数学模型简单,便于计算,可直接得到空间圆参数,计算过程无需进行复杂的迭代求解,从而提高运算效率。

为进一步考虑噪声对算法准确度的影响,选择服从高斯分布的实验点数据进行拟合。噪声点分布在整个平面上而不是在圆附近,按照噪声偏移数据点的情况分为两组实验,如图5(a)、(b)所示。基于CGA方法的数据点拟合结果如图6、图7,结果可以看出:当噪声点越来越偏移数据点时,拟合结果与真实值略有偏差,在误差允许的范围内,可忽略不计。

图5 实验数据点分布

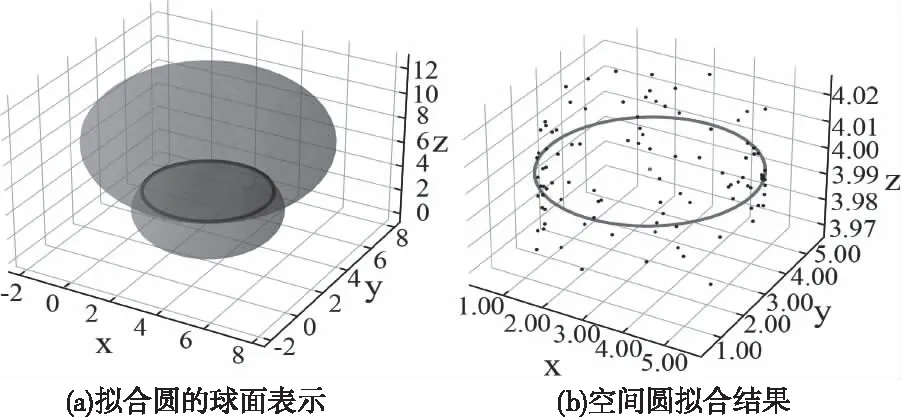
图6 噪声1情况下CGA拟合结果

图7 噪声2情况下CGA拟合结果

由于空间圆拟合算法在欧氏空间是基于空间球体数学模型和平面方程联合得到结果,在计算过程中需要求解大量参数,从而导致运行效率低。而在CGA空间避免了线性计算过程,在简化计算复杂度的同时,处理问题更具几何直观意义。表4中给出了对图6、图7实验数据点三种方法的拟合结果及运行时间。由表4可知,在两种复杂噪声情况下,CGA方法的准确度最高、其次是基于最小二乘的方法、最后是基于SVD的方法。其中噪声2情况的半径误差依次是:4.2088、11.6786、12.1007(×10-3),因此基于CGA方法不仅对含有复杂噪声点数据具有较高的拟合精度,且运行效率最高,运行时间缩短了接近4～5倍。

表4 检测结果及运行时间

4.2 工程仿真验证

为了验证本文方法在实际应用中的实用性,以文献[4]、[5]中的某圆形钢结构的实测参数为例进行验证。采用最小二乘方法、基于SVD方法以及基于CGA方法分别对数据进行拟合计算,数据点三维坐标如表5、6所示。

表5 实例1三维坐标

表6 实例2三维坐标

图8(a)、9(a)分别给出实例1、实例2的CGA拟合结果,具体实测点及拟合圆形如图8(b)、9(b)。实例1中圆形钢结构设计半径为12.2m,利用CGA方法测得拟合圆半径与设计半径误差为3.932mm。另外两种欧氏空间方法得到的拟合圆半径误差均为3.391mm,但是其运行效率低于CGA方法。实例2中圆形物体设计半径为5m,CGA方法测得拟合圆半径误差为3.315mm,最小二乘法为3.293mm,SVD方法为3.296mm。因此,基于CGA方法的空间圆拟合算法满足工程测量的需要,且由于独有的空间特性,运行效率高于欧氏空间。实验结果如表7所示。

图9 CGA拟合结果-实例2

表7 检测结果及运行时间

5 总结

本文在CGA平面圆拟合基础之上,将最小二乘拟合球算法引入到CGA空间,得到CGA空间拟合球算法的新表达,并结合CGA空间特殊的Meet算子,提出了基于共形几何代数的空间圆拟合算法。与文献[14]中基于空间圆特性的最小二乘方法、文献[15]中基于SVD的最小二乘方法相比,本文算法:

1)共形空间对几何实体的处理更加直观,避免了欧氏空间大量求解方程带来的算法冗余问题,算法有效性得到明显提升。

2)将欧氏空间最小二乘拟合球方法映射到CGA空间得到新表达,避免了求解复杂线性方程对算法效率的影响。

3)利用CGA空间Meet算子独特的几何意义计算两个最佳拟合超球,得到最佳拟合空间圆。避免了欧氏空间三维、二维坐标之间的相互转换,算法结构简单,计算效率高。

4)实验表明,本文算法针对数据点较多、噪声分布复杂情况下,算法的检测精度更高,同时运行效率高,工程实用性较强。