基于云边端协同的轻量级作战资源弹性调度算法设计与实现

谷思远，罗雪山，蒋 凯，陈 辉

（1.武警上海总队，上海 200050；2.国防科技大学系统工程学院，长沙 410073）

0 引言

随着云边端协同框架在作战指挥系统中的作用逐渐凸显以及越来越多的现代化网络设备涌现［1-2］，作战系统中的网络应用如数据流转调度、人工智能（artificial intelligence，AI）推理决策和大规模在线数据集成处理等不断出现并被频繁使用［3］。这种类型的网络应用通常具有延迟敏感、资源匮乏和计算密集等特点。网络作战资源类型广泛，包含计算、存储、通信等功能，往往呈现数量众多以及分布较为分散的特点。总体上可以分为云数据中心、固定边缘节点、分散的网络节点以及物联网设备。分散的网络节点以及物联网设备往往资源量较小，但设计得更加灵活。

云边端协同框架正是为了充分发挥分散在网络中的各类作战资源的集成优势［4］，利用云数据中心和边缘节点之间的调度规则来实现资源的充分利用，以更好地服务于各类作战任务应用。其中，每个固定边缘节点通常由接入点（或基站）和边缘服务器组成。然而当下的作战资源云边端协同方案，数据中心即使在固定边缘节点的协调运用下，网络应用的低延迟要求仍然难以随时随地得到保证，原因是，协同框架的资源供给能力与终端节点的需求之间存在供需不匹配的问题。造成这种不匹配的原因大致可以分为以下两类：1）单个边缘节点的资源（如计算、存储资源）不能满足覆盖范围内终端用户的实时需求。从边缘节点部署的角度来看，基础设施的建设往往考虑的是平均资源需求情况，而不是实时情况，尤其是发生作战行动时，作战资源的需求相对集中，呈爆发式增长；2）对某类特定应用的需求暴增时，单靠临近边缘节点的资源都无法应对网络的接入和任务的计算。例如，联合作战场景下，对于在线协同办公的需求增加，仅临近的固定边缘节点可能出现并行接入能力不足以及计算资源不够的问题。以上两类原因分别强调了作战资源在时间和空间分布上的调度难度。

在网络领域，很多研究者致力于通过云边端协同框架的一些优化方法来实现对终端用户应用的快速响应，例如最优服务供给和任务调度算法、最优资源群博弈方法、资源经济型区块链框架等［5-7］。在作战领域，伴随着越来越多的物联网设备（包括无人车、无人飞行器、机器人等［9-11］）的升级转型，这些设备开始不断向智能化发展，也逐渐开发出了网络节点的属性，具备基本的接入、存储、计算功能，并内置不同的网络应用接口。

结合以上的观察，基本构思如下：尽管现有的云边端协同模式，旨在通过在网络边缘预缓存相应的云服务来为终端用户提供低延迟体验。不过在新的作战环境下，面对供需不匹配时仍有很大的改善空间。因此，本文旨在设计一种轻量级调度策略，部署在固定边缘节点，充分发挥物联网设备的网络性能来辅助云边端协同框架，利用其机动性来实现较为灵活的资源供给模式，更好地解决供给不平衡问题。

挑战和贡献：解决作战边缘网络的供需不匹配问题非常具有挑战性，这是因为：1）考虑到激励机制，用什么来刺激潜在的物联网设备作为移动网络节点非常具有挑战性，也是个开放性问题，尤其是涉及到作战时，一切都是服务于作战，而不是各节点自身的利益，很难用市场机制的方法。2）在部署了轻量级调度策略的前提下，如何调度过载的终端任务，以实现最优化指标也同样具有挑战性，因为任务的调度与资源的分配不是割裂开的，在云边端协同框架有了新的资源策略加入的情况下，必然会引发一系列的调度难题。

本文将是第1 个考虑在云边端协同框架基础上部署轻量化作战资源调度策略，来解决网络供需不匹配问题的。主要贡献如下：

1）观测到作战边缘环境下，网络在供需上的时空不匹配问题。此外，观测到作战边缘存在着具备网络功能的物联网设备，设计了云边端协同框架基础上的轻量级作战资源弹性调度策略。

2）为了实现云边端协同框架下的新策略，设计了一个CRI 拍卖机制，来激励物联网设备作为网络资源的辅助，并进行严格的理论分析以证明该设计的可行性。

3）进行大量的实验以验证该设计的卓越性能，即更高的效率和效益。

在本文其他章节中，将逐一介绍框架设计、机制原理、算法特性以及实验评估。

1 轻量级作战资源弹性调度设计

1.1 弹性调度设计概览

因观测到物联网设备具备较为可观的网络资源和机动性，因此，可以充当可移动的边缘计算节点。下页图1 中可发现，边缘节点通常由接入点和边缘云组成，而无人车、无人飞行器和机器人等物联网设备通常具备无线接入的功能，同时具备类似边缘云的计算、存储和应用接口等网络资源［12-13］，可充当移动边缘节点。

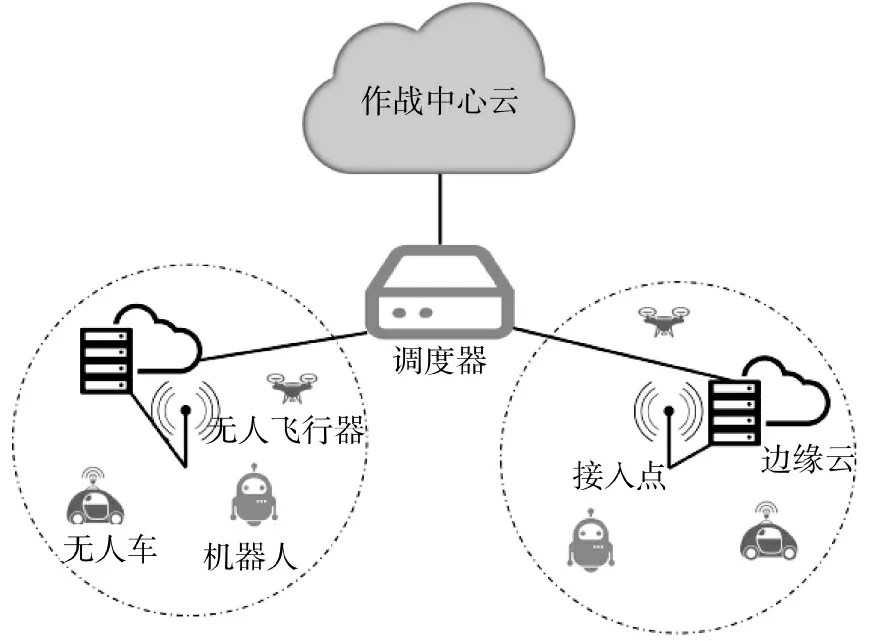
图1 基于云边端协同框架的弹性调度设计Fig.1 Elastic scheduling design based on cloud-edge-end collaboration framework

图1 中的调度器是部署在边缘节点之间的，负责边缘节点与作战中心云和终端用户之间任务调度的应用程序，即将部署的轻量级作战资源调度策略同样是部署在调度器上。调度器应用程序主要是在一个固定时间帧下进行服务缓存决策，以及在一个固定时间片下进行请求调度决策。用于调度决策的时间片往往比时间帧设置小得多，两个时间单位长度都由调度器根据实际情况进行控制。

原有的云边端协同框架主要是通过将单个节点过载的用户请求调度到中心云，或者临近节点进行处理的模式，来解决负载不均衡以及实现最优化和安全服务等一系列问题。如今在新的作战资源背景下，物联网设备成为云边端协同资源框架下的一种有力补充，有助于设计弹性的、灵活的调度策略，广泛提高终端用户的整体服务体验和响应速率。本文旨在云边端协同框架下设计出一个轻量级算法，辅助决策调度，达到网络调度增益的效果。

1.2 符号描述

在这个框架中，集合N={1，2，…，n，…，N}表示固定边缘节点集；连续整数T={0，1，2，…}来描述每个调度决策时间片的起始时间点，其中，连续时间被划分为相等的时间片；集合S={1，2，…，s，…，S}表示在作战网络环境中终端用户可能请求的所有服务类型。在时间片t∊T 内，Mt={1t，2t，…，mt，…，Mt}表示潜在的、可用于服务的移动边缘节点，Ut={1t，2t，…，Ut}表示不能在固定边缘节点及时处理的用户请求，即排队等待的用户请求。对于每个用户请求it∊Ut，调度器将在设计的弹性调度策略下，将请求先依赖于移动节点在网络边缘进行先期处理，从而避免节点间调度和上云处理带来的额外延迟开销。

为了便于参考，本文在表1 中列出了本文的主要符号。

表1 符号描述Table 1 Notation description

1.3 作战网络资源模型

在云边端协同框架基础上部署轻量级作战资源弹性调度决策后，所涉及的总体网络资源如下：

1.3.1 网络链路

战场上的终端用户与固定边缘节点可通过有线或者无线链路连接进行任务上传；移动的物联网设备作为节点，与固定边缘节点之间通过安全的无线链路传输；固定边缘节点之间通过回程网络进行有线连接；作战中心云与固定边缘节点通过主干网连接，但时延大，对于时延敏感的用户请求是难以接受的。因此，调度到远程的作战中心云是一个非常耗时的策略。

1.3.2 缓存资源

固定边缘节点具备灵活的服务缓存能力，可通过容器或虚拟机（virtual machine，VM）等技术实现对作战云上的所有服务类型快速缓存［14-15］。与固定边缘节点不同，移动边缘节点短时间内难以实现服务类型的重新缓存，因此，在决策阶段假定是具有某类特定的服务类型。在未来作战场景下，大量的无人传感设备将会提供较为丰富的服务应用类型，对整体作战资源环境提供更大的支持［16］。作战中心云以强大的存储器缓存各类服务。相比之下，固定边缘节点和移动边缘节点的存储能力较为有限，无法缓存过多的服务。

1.3.3 计算资源

一般来说，固定边缘节点和移动边缘节点的计算能力关乎到CPU、GPU、TPU 等器件性能，用以指代每单位时间内处理的任务数量或处理同一请求所需的时间代价。本文将每个时间片中调度器指定的固定边缘节点无法处理的用户请求，视为潜在移动边缘节点要处理的任务。

2 激励机制设计

为了有序激励移动边缘节点参与到云边端协同框架中，本文设计了可信、互惠和激励的拍卖机制来实现弹性资源调度。一个基本观察是，参与拍卖机制的双方总是在追求自身利益最大化。作战环境背景下不同的是，双方都是为了服务于作战这一个目的，使用拍卖机制是为了提高整体服务效率以及盘活闲散的网络资源。

云边端协同框架下，主要考虑5 类参与方：终端用户、服务提供商、基础设施提供商、移动边缘节点和作战中心云。1）终端用户按照优先级或者规定始终追求最佳服务体验。2）服务提供商负责为终端用户提供广泛的服务。服务提供商可以在固定边缘节点、移动边缘节点、作战中心云等处部署服务。3）基础设施提供商为固定边缘节点和中心云提供计算、存储、通信等网络资源。4）移动边缘节点具备处理部分即时性任务的能力。在收到固定边缘节点指令时，移动边缘节点需要作出计算判断，包括计算任务完成时间（参见式（1）），并给出报价，以及规划自身移动路径。调度器并不决策移动边缘节点的动作，移动边缘节点可以根据接收的任务指令和预测的任务完成时间规划运动轨迹。5）作战中心云缓存终端用户所需的所有服务，并具有庞大的网络资源。在云边端协同框架下，每个时间片由调度器先期决定需要调度到移动节点进行拍卖的任务。在此基础上，将逐步展示图2 所示的CRI 设计细节。

图2 CRI 拍卖机制Fig.2 Auction mechanism of CRI

2.1 终端生成作战任务

2.2 确定候选任务和候选移动节点

拍卖机制需要确保参与方收益，边缘的固定节点和移动节点都需要收益为正才能使系统运行顺畅。此外，还需要考虑作战任务处理的延迟截止期限。算法1 的基本思想就是建立在以上要求确定候选任务和移动节点的，即生成候选集合（candidate sets generation，CSG）。

类似的，表示在远程云中处理任务的完成时间如下：

2.3 分配节点任务

考虑到候选任务集Uct和候选移动边缘节点集Mct，可以发现定价策略并不简单，具体表现在：1）在每个时间段，由于多个任务参与竞价拍卖，因此，不可能简单地使用二价拍卖策略（一种著名的单品拍卖定价策略）［18］。2）除了每个移动边缘节点的出价外，边缘节点还需要考虑利益最大化，这也取决于每个移动边缘节点的任务完成时间。这里，通过以下方式描述将任务it拍卖给mt的固定边缘节点的利益：

如图3（a）所示，本文考虑一个边缘计算环境，包括3 种服务、2 个固定边缘节点、6 个任务和7 个移动边缘节点。一个任务需要候选移动边缘节点为其提供一种对应的服务。因假设中移动节点不能同时处理需要同一服务的多个任务，将投标者定义为具有特定服务的特定移动边缘节点。例如，具有2种服务的图3（a）中的移动边缘节点1 可以被视为图3（b）中的2 个竞标者。图3（b）图中垂直虚线用于区分不同的拍卖节点。图3（b）的红色圆圈包含由同一移动边缘节点生成的竞标节点。因此，在图3（b）中，构造了一个加权二部图（X，Y，E），其中，X 表示任务集，Y 表示竞标节点集，加权链路集E 表示X和Y 之间的关系。使用来表示每个链路的权重。在示例中，目标是使所有固定边缘节点的总利润最大。图3（b）清楚地表明，每个进行拍卖的固定边缘节点都是独立的，由虚线隔离开。因此，可以通过使每个固定边缘节点的利润最大化，来实现总体利润最大化。

图3 示例拍卖问题转化为二部图匹配问题Fig.3 Auction problem to bipartite graph matching problem

本文将加权二部图（X，Y，E）扩展到一个更一般的场景。在每个时间片中，使用X 来表示Uct。此外，用∊Mct×S（mt∊Mct，s∊S）来表示Y 的元素。E的链路用于表示Y 的候选移动边缘节点是否对应X 的任务。通过对图3（a）和图3（b）的观察，可以将原来的图（X，Y，E）拆分成多个子图（Xn，Yn，En），n∊N，并得出以下结论：对于子图（Xn，Yn，En），n∊N 中，它们相互独立，共同构成原始图（X，Y，E）。

为了验证利润最大化问题与加权二部图（X，Y，E）的最大匹配问题等价，本文给出定义1 和定义2［19］，并提出定理1 和定理2：

定义1［完全匹配］图中的匹配是一组独立的链路，其中，没有链路共享相同的节点。匹配的值是匹配中所有链路的权重之和。对于二部图（X，Y，E）及其匹配的Em，如果|X|=|Em|或|Y|=|Em|，则是一个完全匹配。

定义2［最大匹配］对于二部图（X，Y，E），最大匹配就是使得值最大的匹配。

定理1 最大利润等于对应的二部图（X，Y，E）的最大匹配值。如果对应的链路来自于最大匹配问题的匹配，则将对应的任务分配给对应的移动边缘节点。

证明 最大匹配问题就是找到值最大的匹配，匹配中每条链路的值对应于相应利润。因此，最大利润等于相应的二部图（X，Y，E）的最大匹配问题的值。当找到最大匹配时，它的所有链路都表示相应任务的分配。

定理2（X，Y，E）的最大匹配问题可以通过求解所有子图（Xn，Yn，En），n∊N 的最大匹配问题得到。前一个最大匹配的值等于后面子图的最大匹配的值之和。

证明 由于（X，Y，E）的所有子图彼此独立，因此，可以分别计算每个拍卖节点生成的子图。子图的最大匹配值和等于（X，Y，E）的最大匹配值。

算法2 CRI-TSD输入：Uct Mct Bt S t images/BZ_137_1671_2038_1802_2077.png输出：Uwt Mwt Pt 1 图构建2 以Uct 的顺序排序X 节点3 以Mct 和S t 的顺序排序Y 节点4 根据Uct×Mct 和 构建集合E 5 weightxy←images/BZ_137_1485_2381_1615_2420.png6 生成加权二部图G=（X，Y，E），并根据固定边缘节点将它分为一系列子图Gn=（Xn，Yn，En），使其满足G={G1，G2，…，GN}7 最大匹配问题的求解（KM 算法）8 foreach Gn，n∊N do 9 1）初始化和的节点标签10 2）用匈牙利算法搜索一个完全匹配［20］11 3）如果没有找到完全匹配，修改节点标签12 4）重复2）、3）步骤直到找到相等子图的完全匹配13 将最终得到的最大匹配记为14 end 15 Pt←∑n∊N∑X×Y∊Emnweightxy 16 由Emn 得到Uwt Mwt 17 返回结果：Uwt Mwt Pt

基于定理1 和定理2，可以通过求解一系列图匹配问题来解决利润最大化问题。因此，本文将重点放在单个节点的最大匹配问题上，并在算法2 中给出了求解方法，以此来确定任务集合（task sets determination，TSD）。对于，本文假设定价等于任务分配过程中的出价。如算法2 所示，将此过程分为两个步骤：图构造和最大匹配问题求解。在第1 步（参考1～6 行），根据已知的Uct，Mct，St，来构造加权二部图G。在第2 步（参考7～14行），采用著名的Kuhn-Munkres（KM）算法［21］在时间复杂度O（max{|X|3，|Y|3}）上找到最大匹配。Emn是En的一个子集，表示完全匹配，也是找到的最大匹配。此外，第15 行中的Pt表示时间片t 中最大利润。最后，得到Uw（tMwt），这是赢家的任务（移动边缘节点）的集合。

因此，在算法2 中，在第2 步中得出时间复杂度为O（N*max{|Xn|3，|Yn|3}），这比O（max{|X|3，|Y|3}）好很多（即求解G 图的时间）。然后计算第15 行的最大利润值，得到16 行中的优胜者任务和移动边缘节点。

2.4 处理任务以及结算

任务分配完成后，优胜者移动边缘节点将处理相应的用户请求并将结果返回给终端用户。在此阶段，值得注意的是，移动边缘节点是否将执行处理操作以及如何确保这一点。如图2 所示，除了生成候选集外，移动边缘节点还需要向固定边缘节点提交参与证书，即参与证明（proof of participation，PoP）。PoP 可以是设备标识号，可以用来识别和跟踪唯一的移动边缘节点。那么，如果提交PoP 并成为赢家的移动边缘节点放弃任务，将损害其信誉，甚至可能受到追责等不可估量后果。另外，如果移动边缘节点没有在保证的时间内完成任务，则边缘节点将得到补偿。因此，可以使用PoP 来确保移动边缘节点的行为诚实。

当处理完所有获胜者任务Uwt时，固定边缘节点应向获胜者Mwt结算奖励。为使过程不可抵赖，使用分配证明（proof of assignment，PoA），在任务处理之前发送给获胜者。PoA 可以记录固定边缘节点向移动边缘节点分配任务的事实，在此基础上，固定边缘节点在完成任务处理后，必须支付所分配任务的移动边缘节点的工作量。

3 CRI 设计分析

3.1 算法复杂度分析

算法3 CRI输入：Ut Mt S t Bt V t images/BZ_138_1739_478_1870_517.png输出：Uwt Mwt Pt 1 （Uct-Mct）←CRI-CSG（Ut，Mt，S t，Bt，V t）2 （Uwt，Mwt，Pt）←CRI-TSD（Uct，Mct，Bt，St，images/BZ_138_1944_637_2074_676.png）3 返回结果：Uwt Mwt Pt

算法3 包含整个拍卖过程，即候选集生成（算法1）和任务分配确定阶段（算法2）。在算法1 的第9 行，将中的移动边缘节点进行排序，时间复杂度为O（||log（||））。在第10 行中的for 循环，时间复杂度为O（||）。因此，第6 行中的for 循环的时间复杂度为O（Ut|（|1+log（||）））。因此，算法1 时间复杂度为O（Ut|（|1+log（||）））。

在算法2 中，KM 算法的时间复杂度为O（N*max{|Xn|3，|Yn|3}）。第2 行中的排序X 节点时间复杂度为O（|Uct|log（|Uct|）），第3 行中的排序Y 节点时间复杂度为O（|Mct×S|log（|Mct×S|））。因此，算法2 的总体时间复杂度为O（N*max{|Xn|3，|Yn|3}+|Uct|log（|Uct|）+|Mct×S|log（|Mct×S|））。

由上可得算法3 中的CRI 机制运行的总体时间复杂度为O（Ut|（|1+log（||））+N*max{|Xn|3，|Yn|3}+|Uct|log（|Uct|）+|Mct×S|log（|Mct×S|））。换句话说，CRI 可以在多项式时间内收敛到最终分配和定价结果。

3.2 机制期望属性

为了验证CRI 拍卖机制的合理性，以下定理证明应满足的期望属性。

定理3 CRI 满足个体理性。

对于竞拍者（即参与竞拍的移动边缘节点），使用等式（4）中的来表示每个竞拍者的利润。现在让=≥，则≥0 始终成立，因此，投标人的利润是非负的。从竞买方/移动边缘节点的角度来看，非负利润实际上促进了闲置资源的有效利用。因此，可以充分利用潜在的移动边缘节点。

以上两个结论共同证明了CRI 满足个体理性。

定理4 CRI 满足真实性。

证明CRI 设计的特殊之处在于只追求拍卖人的利润最大化，而不是竞拍人。投标者根据成本等情况确定出价。然而，由于是密封拍卖［22］，竞拍者不知道对方的出价、计算能力和其他信息。如果哄抬价格，很可能导致被排除在候选集外，从而无法获益。因此，可以推断其出价是基本合理的。在Bt的基础上，为了使整个域的利润最大化，每个拍卖商（固定边缘节点）用KM 算法来决定中标者以使自己的利润最大化。由于定价策略是基于每个竞买人的出价，所以固定边缘节点的决策不会损害竞买人的利润。从上面的推理可以看出，拍卖人和竞拍人都必须满足真实性，才能使双方收益最大化。

定理5 CRI 满足利润最大化。

结合上述期望的经济属性与计算复杂度，从理论上保证了CRI 设计的可行性。之后将用仿真实验来验证其优越性。

4 实验验证

4.1 实验设置

1）网络构建。因为CRI 设计并没有假设额外的用户需求、任务价值和移动边缘节点出价。因此，验证结果对任何可能的数据集都是有效的。为了一般性，随机生成用户请求的价值和每个任务的相应出价，它们都在（0，1］内服从均匀分布。此外，引入了参数α，它是候选任务与边缘计算环境中生成的所有用户请求的比率。实际上，α 反映了固定边缘节点的资源短缺情况，其中α 的值越大，资源就越稀缺。本文使用α 随机生成候选任务集。此外，本文还引入了参数β，即候选移动边缘节点与所有覆盖到的移动边缘节点的比率。而β 可以用来反映应急能力，即数值越大，应急能力越强。α 和β 都随时间动态变化，目标是生成α 和β 来接近边缘计算环境，这意味着供需基本平衡。

在实验装置中，模拟了图4（a）中的供需不匹配情况。如前所述，利用成都出租车用户的数据集［23］模拟用户请求的需求，并设置供给能力。图4（a）中发现由于固定边缘节点的资源在一天中的某些时段（如0～8 点钟）被过度调配，而在某些时段（如18∶00 到21∶00）资源短缺，供需不匹配严重，比率和表示如下：

图4 数据图Fig.4 Data graph

图4（b）显示β 的值随α 的值而变化，根据［0，0.1］内的均匀分布设置的值。

算法4 GA输入：Ut Mt S t Bt V t images/BZ_139_1739_1746_1870_1785.png输出：Uwt Mwt Pt 1（Uct-Mct）←CRI-CSG（Ut，Mt，S t，Bt，V t）2 CRI-TSD 的1～6 行3 贪婪分配算法4 foreach Gn，n∊N do 5 1）初始化Xn 和Yn 的节点标签6 2）寻找最大权重的链路，并移除与相应节点相关的链路7 3）继续搜索剩余链路，重复2）直到子图中没有链路8 4）记录2）、3）步骤中搜索到的所有链路9 将最终得到的匹配记为Engreedy 10 Pt←∑n∊N∑X×Y∊Egreedyn weightxy 11 从Engreedy 得到Uwt Mwt 12 返回结果：Uwt Mwt Pt

2）对比算法。为了体现CRI 算法的优越性能，将其与两个基准算法进行了比较：1）贪婪分配（greedy assignment，GA）：该算法使用贪婪分配算法（参考算法4 的4～10 行）来代替算法3 的KM 算法。第9 行中的Engreedy是En的子集，表示贪婪算法搜索的匹配项。可以看到贪婪分配算法的时间复杂度是O（N*|Xn×Yn|2log2|Xn×Yn|）。2）边云模式（all up to clouds，AC）：旨在以固定边缘节点和远程云的能力响应所有用户的请求，这一点已经在许多工作中进行了研究［6，24］。

4.2 算法性能

为了展示算法性能，将其与两个基准进行比较。严格分析3 个指标，并进行了一般性评估。

1）任务完成率。图5（a）显示了不同数目的候选移动边缘节点和任务时的基准算法和CRI 算法的平均任务完成率（Task Completion Rate，TCR）。例如，图5（a）中的350*500 意味着随机生成350 个候选移动边缘节点和500 个候选任务。Y 轴的任务完成率表示候选任务的完成率。结果表明，CRI 和GA的TCR 远高于AC 的TCR，说明在边缘计算环境中引入拍卖机制可以显著提高TCR。同时，发现CRI的TCR 略高于GA 的TCR，并且发现CRI 的KM 算法正在寻找等价子图的完全匹配，而GA 的贪婪分配算法可能不会搜索到这样的匹配。另外，可以看到TCR 随着候选移动边缘节点的增加而上升，随着候选任务的增加而降低，这可以解释为候选移动边缘节点越多（待响应的候选任务越少），能够响应的任务越多（TCR 越高）。因此，得出结论，CRI 设计可以显著提高固定边缘节点的服务质量。

图5 CRI/GA/AC 对应任务完成率和运营者利润的变化Fig.5 TCR and profit of CRI/GA/AC

2）效益。图5（b）表示固定边缘节点通过改变候选移动边缘节点和任务的数量可以获得的平均效益。结果表明，CRI 算法的收益高于GA 和AC 的收益，高于GA 的收益是因为CRI 的KM 算法追求最大匹配，而GA 的贪婪算法可能得不到最优解。而高于AC 的利润是因为虽然每个被响应的任务都能获得更多的利润，但是总利润会因为TCR 的降低而降低。因此，CRI 设计的利润仍然优于其他两个基准。此外，由于同步TCR 的提高，图5（b）中的所有效益都随着候选移动边缘节点的增加而增加。但是，随着候选任务数的增加，利润先增加后减少。原因是TCR 在下降，但候选任务的基数在上升。因此，得出结论，CRI 设计在经济上对固定边缘节点有利。

3）计算效率。为了确认之前的时间复杂性的分析，在表2 中记录了不同设置下的CRI 运行时间。对于每个设置，本文随机生成50 个实例并记录平均结果。使用python3.6 和Intel（R）Core（TM）i7-8750H 处理器、16 GB 内存运行所有测试。验证了CRI 的算法3 分别对于候选任务集和移动边缘节点集在多项式时间内收敛。表3 显示了GA 的平均运行时间，结果表明CRI 和GA 都是计算效率高的，GA 并不比CRI好。至于AC，虽然不需要花费拍卖过程的时间，但随后表明可能会在其他指标表现略差。

表2 CRI 的运行时间（N=10）Table 2 Algorithm run time of CRI（N=10）

表3 GA 的运行时间（N=10）Table 3 Algorithm run time of GA（N=10）

总的来说，与其他两个基准相比，本文的CRI算法在上述3 个指标上都有更好的性能。这些指标从服务质量、经济效益和计算效率3 个方面反映了CRI 设计的优势。因此，可以得出结论：将CRI应用到云边端协同框架下的弹性调度系统中，可以通过获得更高的TCR 和更高的效益，来提高固定边缘节点整体的服务质量（quality of service，QoS）。

4.3 经济性能

1）个体理性。定理3 证明了CRI 是个体理性的，这意味着每个赢家任务的价值高于收费价格（参见下页图6（a）），而每个赢家移动边缘节点收到不低于其处理相应任务的成本的出价（参见图6（b））。给出了图6（a）中赢家任务的价值和价格，以及图6（b）中赢家移动边缘节点的出价和成本。结果表明，获胜的移动边缘节点获得了正的收益，即从CRI 中获益。此外，由于每个赢家任务的效用都是正的，因此，云边端环境全局也是收益的。因此，移动边缘节点愿意支持固定边缘节点，并且调度器也倾向于拍卖一些固定边缘节点无法处理的任务。

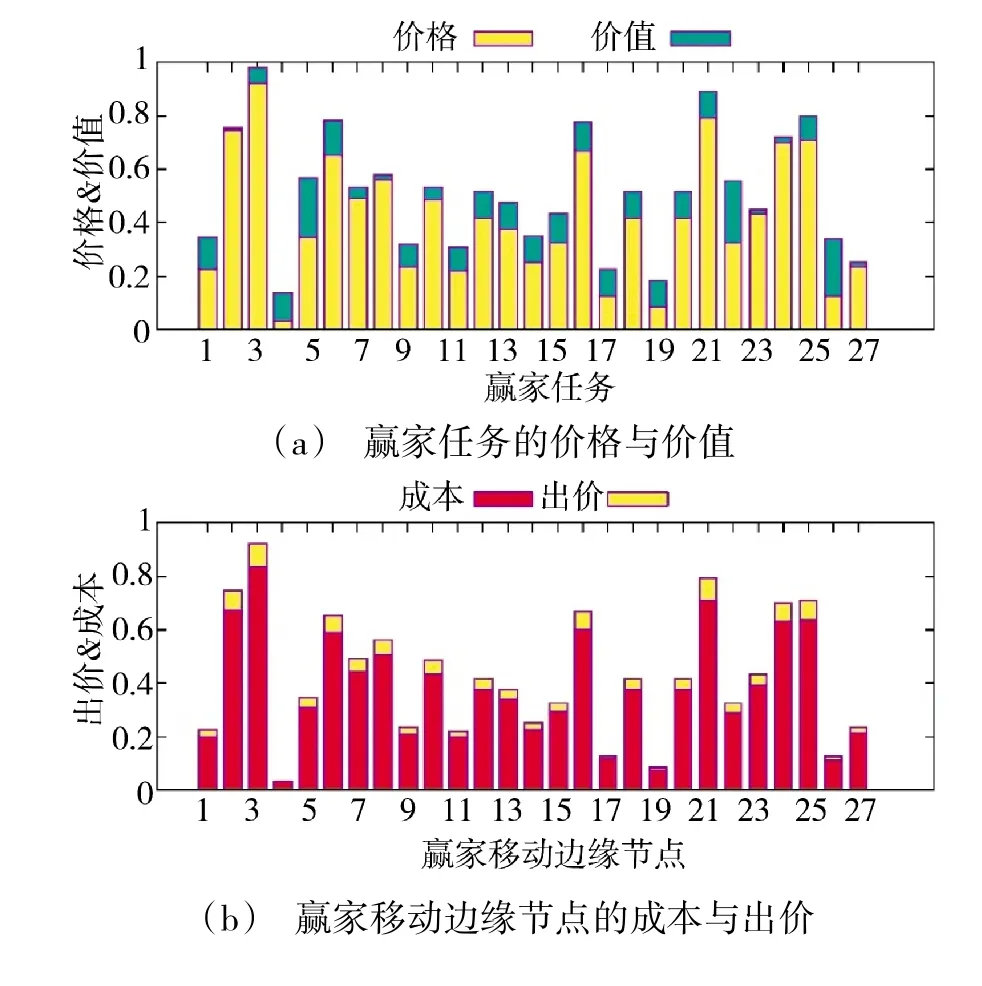
图6 CRI 的个体理性Fig.6 Individual rationality of CRI

2）真实性。为了验证定理4，随机选取一个移动边缘节点来研究其效益在出价不同时的变化。如图7（a）所示，显示了当其出价为0.448 且成本为0.295 时，移动边缘节点是赢家。因此，移动边缘节点获得效益0.153。然后，改变这个移动边缘节点的出价重新测试。结果表明，当出价低于0.448 时，该移动边缘节点仍能赢得拍卖，但当出价超过0.448美元时，该节点将失去拍卖。可以看出，移动边缘节点无论出价多少，都无法提高其效用。然而，从对所有移动边缘节点的测试中，发现很少有像这样的情况：当出价为0.557、成本为0.306 时，移动边缘节点仍然可以通过提高出价来提高其效用。在此，虽然所有的移动边缘节点都可以灵活地调整其出价，但也存在很大的竞价失败风险，实验测试因为提价丢掉竞拍的概率高达97.87%。因此，理性的移动边缘节点将会真实地出价。此外，可以在两种情况下推断边缘节点的真实性：1）如果价格低于中标人的出价，将损害固定边缘节点的信誉，这是极力避免的；2）如果价格高于中标人的出价，则会损害固定边缘节点的效益。综上所述，CRI 可以保证移动边缘节点和固定边缘节点的真实性，因为不真实行为也无法提高效用，并且会因此失去继续参与的权利。

图7 CRI 的真实性和利益最大化Fig.7 Truthfulness and profit maximization of CRI

3）利益最大化。为了验证定理5，使用图7（b）中的案例c，其中，中标者出价为0.44，赢家任务的价值为0.55。如果price<0.44，则会损害固定边缘节点的信誉（参见定理4），这是极力避免的。如果price≥0.44，则固定边缘节点无法从任务中获得更多好处（请参阅等式（3））。因此，CRI 保证了固定边缘节点从每个赢家任务中获得的利益最大化。

通过以上的仿真实验，验证了实验结果与理论证明的一致性，并在今后的工作中，对真实场景的模拟也是必要的。

5 结论

边云协同框架的设计目的是为战场环境用户提供“随时随地”的低延迟服务。为了应对固定边缘节点的资源局限和用户需求的不确定性挑战，引入了弹性调度设计，旨在解决边缘端供需不匹配不平衡的问题。同时，用实验验证了机制设计的合理性、真实性和效益最大化等性能，数值结果也真实反映了该设计可以提高用户的体验质量（quality of experience，QoE）。