基于确定性梯度策略的固定翼飞行器博弈方法

杨 洋，魏耀涛，程培传

（1.解放军91948 部队，海口 570100；2.北京理工大学，北京 100081）

0 引言

近年来，随着现代控制理论和工业设计的不断进步，飞行器技术在军事、民用领域得到了广泛的应用。借助大数据和数据驱动的方法，基于信息论和自动控制的飞行器展现出卓越的飞行性能和高效的控制能力，为军事作战、信息探测、地理测绘等领域带来重要影响。尤其在现代化的军事行动中，飞行器能够替代专业人员执行各种特定任务，有效避免人员伤亡，成为军事战略的关键组成部分。数据驱动的飞行器对抗决策方式成为飞行器作战过程中的关键技术之一。因此，控制方法作为固定翼飞行器实现决策的关键技术，也在大数据和数据驱动的背景下得到了进一步的发展和应用。

固定翼飞行器的控制方法主要可以划分为线性控制、非线性控制和强化学习3 个主要类别。线性控制方法常用的包括PID 控制、LQR 控制和H∞控制等［1-3］。线性方法具有简单有效的特点，但在实际应用中，很多系统具有非线性的特性，如鲁棒性差、非线性耦合、非对称性等。为了更好地描述和处理这些复杂系统，非线性控制方法应运而生。非线性控制方法主要包括滑膜控制、模糊控制和非线性模型预测控制等。

强化学习方法是一种适用于复杂环境下的智能控制方法，可以自主学习控制策略并逐步优化，适用于需要自主学习的飞行任务。强化学习涉及到智能体（agent）与环境（environment）之间的交互，智能体通过试错的方式不断地尝试执行各种操作，从而逐步学习如何获得最大化的奖励或最小化的惩罚。

近年来，伴随深度强化学习（deep reinforcement learning，DRL）取得显著成绩，深度强化学习的应用场景越来越广泛。它利用深度神经网络拟合难以学习的价值函数或最优策略，使其在处理复杂问题和大规模数据方面更有优势。2013 年DeepMind 提出深度Q 网络（deep Q-networks，DQN）［3］，并于2015年在《Nature》上发表。为了解决Q-learning 不适宜处理高维数据［4］，奖励函数需要人为地去设定等不足，作者将Q-learning 与卷积神经网络相结合，用神经网络去拟合一个奖励函数。最后发现经过训练的DQN 可以Atari 2600 的多个游戏中表现得比人类专家更好，这标志着深度强化学习的诞生，展示了深度学习在强化学习领域的强大潜力。随之而来的产生了许多DQN 的变种，如DRQN、Double DQN、Dueling DQN 等［5-7］。

尽管在很多场景中DQN 及其变种都能取得不错的效果，但DQN 作为一种基于值的强化学习方法，在处理连续动作空间的问题上显得左支右绌。因而，基于策略梯度的强化学习方法被发掘了出来。在2015 年，LILLICRAP 等提出了深度确定性策略梯度（deep deterministic policy gradient，DDPG）算法，将Deep-Learning 成功地应用于连续动作领域［8］。它是一种基于演员-评论家（Actor-Critic）的算法，实验结果表明使用相同的学习算法、网络架构和超参数，提出的算法解决了20 多个模拟物理任务，包括经典问题，如推车摆动、灵巧操作、腿部移动和汽车驾驶。随后，SCHULMAN 等提出一种信任区域策略优化（trust region policy optimization，TRPO）算法，优化了梯度更新时选择步长的问题，给出了一种优化控制策略的方法，并保证单调改进［9］。该算法对于优化神经网络等大型非线性策略非常有效。在TRPO算法的基础上，SCHULMAN 等于2017 年提出了一种改良算法（proximal policy optimization，PPO），PPO算法通过削减连续策略的KL 散度，确保了参数更新时的稳定。为了解决DDPG 对Q 值过度估计的问题，FUJIMOTO 等在2018 年提出的TD3（twin delayed deep deterministic policy gradient）算法，TD3使用双Q 网络，延迟Actor 网络更新，在目标Actor 网络输出的动作上增加噪声，使得算法更加稳定。BARTH-MARON 等在2018 年提出了D4PG（distributed distributional deterministic policy gradients），D4PG 在DDPG 的基础上将单一Actor 网络扩展至多个，并将Critic 由一个函数扩展成一个分布，使得D4PG 可以应用于分布式。

因为能够更好地处理连续动作空间和高维状态空间，从而更好地控制飞行器的姿态和运动轨迹，深度强化学习算法在固定翼飞行器控制领域得到了日益广泛的应用和认可。ZHANG 等使用DDPG直接对固定翼飞行器的控制机进行建模，改善了飞行品质，实现了对固定翼飞行器巡航飞行一体化的控制［10］。YANG 等同样在DDPG 的基础上，通过建立避障策略知识库，缩短DDPG 的训练时间，使得无人机满足在复杂环境下的实时避障需求［11］。YANG等提出了一种基于深度强化学习的目标跟踪方法，将无人机电机转速作为PPO 算法的输入，实现端到端的跟踪。实验证明该方法满足跟踪要求，也有很强的鲁棒性。

DDPG 作为经典的适用于连续动作空间的强化学习算法，在飞行器控制领域的应用前景十分广阔。在DDPG 算法中，动作的输入可以是飞行器的角度，推力等指令，通过训练，可以实现对飞行器姿态和位置的精确控制。此外，DDPG 算法可以对控制系统进行端到端的学习，不需要对系统进行过多的建模和假设，更加适用于复杂、多变的飞行环境。

本文将DDPG 算法应用于飞行器控制，并通过仿真实验验证了该方法在数据驱动环境下的可行性和有效性。通过这种基于大数据和数据驱动的动态控制方法，飞行器能够在复杂环境中实现自主决策，并显著提升与敌方对抗的成功率，为飞行器技术在军事和民用领域的广泛应用提供了强有力的支持。

1 固定翼飞行器模型构建

1.1 飞行器参数分析

基于现有装备平台的典型参数，对仿真实验所用的固定翼飞行器模型基本参数设计如表1 所示：

对仿真实验所用的固定翼飞行器模型性能参数设计如表2 所示：

1.2 飞行器控制系统设计

固定翼飞行器的控制原理通常包括姿态控制。姿态控制是飞行器飞行稳定性的基础。姿态控制旨在稳定飞行器的俯仰、滚转和偏航角，以确保飞行器在空中保持平衡和稳定的飞行状态。

姿态控制通常采用内环反馈控制器来实现，其控制变量为飞行器的三轴角速度。姿态控制方式如图1 所示。

图1 固定翼飞行器姿态控制原理Fig.1 Attitude control principle of fixed-wing aircraft

在本文中，通过对飞行器参数进行分析，设计了飞行器控制系统的自动驾驶仪。对于固定翼飞行器，控制系统接收速度大小指令以及速度方向上的倾角大小和偏角大小指令，从而实现对飞行器航向的控制，以完成飞行任务。

1.3 飞行器博弈场景设计

本文研究的博弈类型属于动态博弈，允许博弈双方在不同时间点作出决策。博弈的主体为红方双方飞行器。

在作战背景中，本文假设如下博弈场景：在该场景下，固定翼飞行器根据作战目标不同分为红蓝两方，红方为防守方，蓝方为进攻方。考虑到飞行速度，飞行姿态以及仿真资源等因素，将对抗区域设置为图2 所示的矩形区域，攻击纵深为L=5 km，通道带宽（突防走廊）为L=3 km，飞行高度为H=1 km。在初始时刻，红蓝双方的起飞点分别在AB，CD 边线附近，其中，红蓝双方各有1 架飞行器。

图2 博弈场景示意图Fig.2 Schematic diagram of game scene

假设红蓝双方飞行器是同构的，但飞行性能上有所不同。蓝方作为进攻方，由智能算法控制其飞行轨迹，飞行受到对抗区域的约束，不可越过AB，CD两条边或超过飞行高度，也不可接触地面，越过边界则视为损毁。红方作为防守方，由智能算法控制，其飞行不受水平面上对抗区域ABCD 或是高度上限的限制，可以自由飞行，但接触地面也视为坠毁。

针对蓝方飞行器，红方采用硬杀伤的方法打击蓝方飞行器。硬杀伤包括碰撞和自爆两种方式。在本实验中，红方飞行器选择自爆毁伤蓝方飞行器，当红方飞行器与蓝方飞行器距离小于一定范围时，判定为毁伤蓝方飞行器，如图3 所示。自爆后，双方飞行器退出战斗。

图3 飞行器攻击方式Fig.3 Aircraft attack method

当蓝方飞行器被击毁或蓝方飞行器突破红方飞行器拦截范围，博弈结束。

在飞行器飞行过程中，在某一时刻对控制系统输入的是速度的大小以及速度方向上的倾角和偏角，控制系统根据上述指令，输出飞行器舵偏角控制信号，根据运动学动力学模型计算出下一时刻飞行器的运动信息，包括飞行器在NED 坐标系下的位置坐标，以及在NED 坐标系下的速度矢量等。通过上述操作，飞行器在控制系统下完成飞行操作。

2 固定翼飞行器控制方法设计

2.1 动作空间与奖励函数设计

动作空间的定义直接决定了智能体的行为选择范围。飞行器动作空间的设计需要考虑控制系统的控制方式。由于实验中控制系统的控制模式是控制飞行器的航向，即算法要向控制系统输入飞行器的速度倾角指令，速度偏角指令和速度大小指令，控制系统则输出飞行器在NED 坐标系下的位置、速度等信息。所以算法的输出也是要与速度倾角、速度偏角和速度相关的量。为了保证飞机飞行的平稳，上述3 个量在相邻两个时刻内不能剧烈变化，因此，针对每一架红方飞行器，它动作的输出是一个较小的改变量，而不是速度倾角、速度偏角和速度具体的数值。这个改变量被定义为一个三维向量：［theta_v_c_ch（速度倾角改变量），psi_v_c_ch（速度偏角改变量），V_c_ch（速度大小改变量）］。

在强化学习中奖励函数指环境返回给智能体的一个标量值，用于评估智能体的行为好坏。奖励函数是强化学习的关键之一，它决定了智能体的学习目标和优化方向。

在本实验中，考虑到红方飞行器的作战目标是击毁蓝方飞行器，因此，每架红方飞行器的奖励函数的设计原则如下：

1）为了让红方飞行器能够靠近蓝方飞行器，设计一个和距离相关的奖励。即reward=-distance，distance 表示距离红方飞行器最近的蓝方飞行器的距离，单位为km，且为了防止飞行器因为想获得更多奖励而选择绕路，故将奖励值设计为距离的负数。

2）为了让红方飞行器能够击毁蓝方飞行器从而获得对抗的胜利，设计一个与击毁蓝方飞行器相关的奖励。当红方飞行器距离最近的蓝方飞行器距离小于100 m 时，蓝方飞行器进入红方飞行器的攻击范围，当红方飞行器击毁一架蓝方飞行器时，获得一个奖励reward=50。

3）为了让红方飞行器能够更快地靠近蓝方飞行器，考虑到飞行器的刚体运动特性，设计一个与飞行器速度朝向相关的奖励函数。当红方飞行器速度方向向量与红蓝双方所在位置连线向量夹角小于5°时，可判定为红方飞行器正在精确地朝向蓝方无人机，得到一个正奖励reward=5，否则得到一个负奖励reward=-3。

4）为了让红方飞行器不远离作战范围，设定区域边界，当红方飞行器的运动位置超过区域边界时得到一个较大的负奖励reward=-100。

2.2 基于DDPG 的固定翼飞行器动态博弈方法

将红方飞行器看作一个用深度强化学习算法训练的智能体。在该模型下，训练流程包括强化学习环境的初始化与强化学习环境与算法的交互。

本实验所采用的深度强化学习算法是DDPG算法，通过对算法输入输出接口的设计和算法内部的改进，将其运用在飞行器对抗环境中，其主要流程如下页图4 所示。

该算法中，红方飞行器有一个Actor 网络和一个Critic 网络，同时还有一个目标Actor 网络和一个目标Critic 网络，用于稳定参数更新。每个网络都是全连接神经网络。

训练时，在算法初始阶段，存在一个经验回放缓冲区（reply buffer），环境输出红方飞行器状态给Actor 网络，Actor 网络输出飞行器预测动作。然后将飞行器动作合并为动作向量，传递给环境执行动作。环境返回奖励和下一个状态。当前动作、当前状态、奖励和下一个状态被添加到经验回放缓冲区中。当经验回放缓冲区积累到一定数量时，从中采样一定量的数据用于训练更新网络。更新网络时，Critic 网络接收飞行器的动作和状态信息，输出智能体的Q 值，再使用target Critic 网络计算下一个状态下的飞行器的目标Q 值，由Q 值、奖励值和目标Q值更新网络参数，提高Critic 网络的评判水平。Actor网络接收其对应Critic 网络传递来的Q 值，目标是最大化Q 值，以得到预期最大奖励。Actor 网络和Critic 网络通过在训练交互中的不断更新，相互促进，提高Actor 网络输出动作的质量和Critic 网络评估动作的准确性。测试时，不需要更新网络，只需要将状态输入到参数固定的Actor 网络，就可以得到动作指令，控制飞行器飞行轨迹。这种基于数据驱动的训练方法，使得飞行器在复杂环境中能够通过学习和优化，自主作出决策。

3 仿真结果与分析

为了探究如何使用强化学习算法控制飞行器得到更好的博弈对抗效果。实验分别在二维空间和三维空间下展开博弈仿真。

训练中所采用的硬件配置包括如下：Intel（R）Core（TM）i5-9300H CPU@2.40 GHz 处理器，NVIDIA GeForce GTX 1650 显卡。算法实现采用Tensorflow深度学习框架。

3.1 二维空间仿真结果分析

在该实验场景下，飞行器的动作空间为速度改变量和速度方向上偏角改变量这两个自由度。初始化时，红方飞行器的位置为（x1，y1），其中，x1∊（0，50），y1=0，单位为m，速度为50 m/s，偏航角为0°，即沿x 轴正方向飞行。蓝方飞行器的位置为（x2，y2），其中x2∊（4 950，5 000），y2∊（-500，500），单位为m，速度为40 m/s，偏航角为180°，即沿x 轴负方向飞行。

二维空间下的DDPG 算法的相关参数设计如表3 所示：

表3 DDPG 算法超参数设计Table 3 DDPG algorithm hyperparameter design

二维空间下的网络的设定参数如表4 所示：

表4 神经网络参数设定Table 4 Neural network parameter setting

其中，输入层和隐藏层的激活函数为relu，Actor网络输出层没有激活函数，Critic 网络输出层的激活函数是tanh，将动作空间的输出限制在一定范围内。

红方固定翼飞行器得到的奖励值曲线如图5所示：

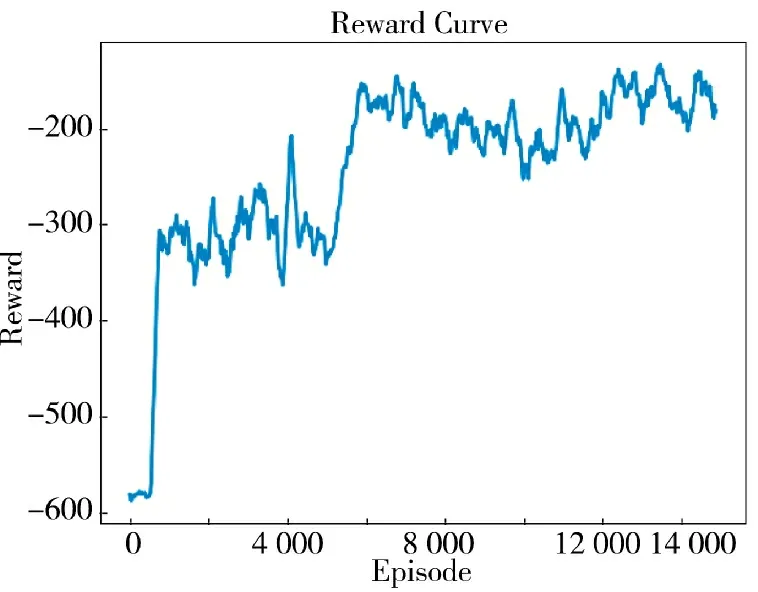
图5 二维空间红方固定翼飞行器奖励值曲线Fig.5 Two-dimensional space red square fixed-wing aircraft reward value curve

可以看到，在训练初期，红方飞行器在环境中随机探索，网络不进行更新，因此，在每个episode 中得到的总奖励值大多时候都比较低。当episode 进行到600 个回合左右时，经验回放缓冲区已经积累了大量的训练数据，网络开始进行参数更新。随着网络参数的更新，红方飞行器的奖励值迅速提升，逐步学习到更优的动作策略。当训练进行到约6 000个回合时，奖励值逐渐趋于稳定，达到了收敛状态。奖励值的收敛意味着飞行器学习到了一个相对稳定的策略。这种数据驱动的训练方法充分利用了大数据的信息，使得飞行器在复杂环境中能够通过学习和优化，逐步提升控制策略的质量。

训练完成后保存算法模型的参数文件，在测试过程中，固定红方飞行器的位置，随机初始化蓝方飞行器的位置，并进行1 000 次测试，统计实验结果。结果表明，红方飞行器击毁蓝方飞行器的次数为569 次，成功率达到56.9%。

随机抽取两次红方胜利的对抗实验，并将结果展示如下：

从图6、图7 中可以观察到以下情况：当蓝方飞行器在一定范围内随机初始化时，即使每一轮测试中蓝方飞行器的位置相距较远，这并不会对红方飞行器的决策造成很大的影响。红方飞行器仍能以较高的准确率追踪并击毁蓝方飞行器。这表明算法在应对环境中位置改变方面具有鲁棒性，不容易受到干扰。

图6 蓝方飞行器初始位置（x2，y2）=（5 000，500）Fig.6 The initial position of the blue aircraft（x2，y2）=（5 000，500）

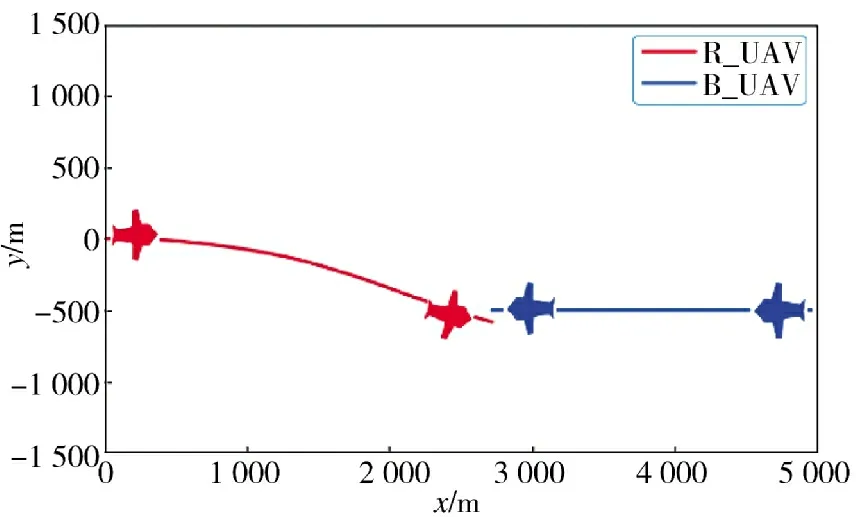
图7 蓝方飞行器初始位置（x2，y2）=（5 000，-500）Fig.7 The initial position of the blue aircraft（x2，y2）=（5 000，-500）

3.2 三维空间仿真结果分析

在该实验场景下，飞行器的动作空间为速度改变量、速度方向上偏角改变量和速度方向上倾角改变量这3 个自由度。初始化时，红方飞行器的位置为（x1，y1，z1），其中，x1∊（0，50），y1=0，z1=-500，单位为m，速度为50 m/s，偏航角为0°，即沿x 轴正方向飞行。蓝方飞行器的位置为（x2，y2，z2），其中，x2∊（4 950，5 000），y2∊（-500，500），z2∊（-750，-250），单位为m，速度为40 m/s，偏航角为180°，即沿x 轴负方向飞行，由于实验所处的NED 坐标系下，Z 轴指向地面的垂直向下方向，因此，飞行器的高度h 用-z2表示。

算法训练过程与二维空间仿真相似，但为了应对动作空间和状态空间的扩大，对算法的训练过程进行了一些调整，以适应更大规模的数据。具体来说，将Actor 网络和Critic 网络的隐藏层大小设置为256，增大batch_size，并且增加了训练的episode 数量，以提高算法的收敛性和性能。训练后，红方固定翼飞行器得到的奖励值曲线如图8 所示。

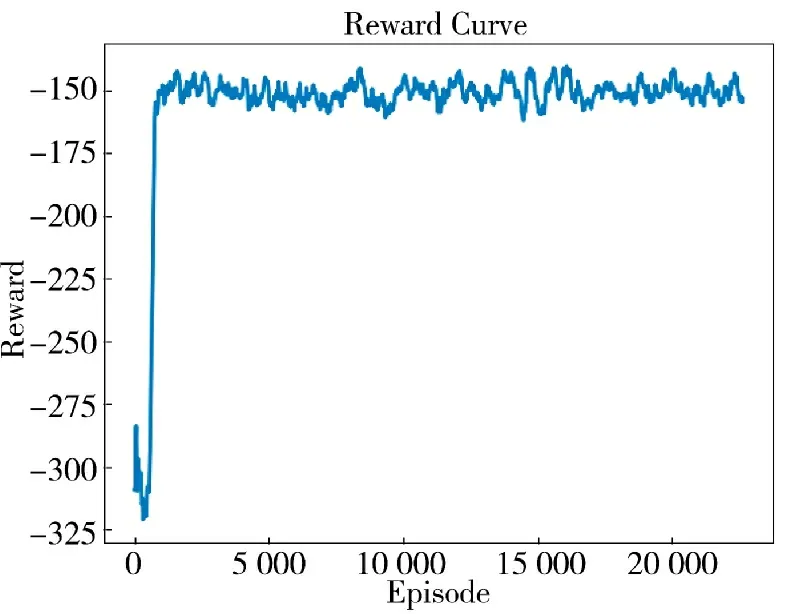
图8 三维空间红方固定翼飞行器奖励值曲线Fig.8 Three-dimensional space red square fixed-wing aircraft reward value curve

观察奖励值曲线，可以看到训练过程与二维空间仿真相似。在初始阶段，奖励值呈现较大的波动，这是由于飞行器在探索未知空间时面临较高的不确定性。经过少量探索后，算法很快得到了收敛，飞行器学习到了优秀且稳定的策略。这表明，通过大规模数据的训练和优化，飞行器能够快速适应复杂环境，并优化决策策略。

训练完成后，在测试阶段，随机初始化蓝方飞行器的位置，同样进行1 000 次测试，统计对抗结果，计算得出红方的对抗胜率为28.6%。相较在二维空间下，三维空间的复杂性增加了任务的难度，胜率有所下降。

为了更详细地了解对抗实验的结果，随机抽取3 次红方胜利的对抗实验，并随机选择了蓝方飞行器初始化的位置，将结果展示如图9～图11 所示。

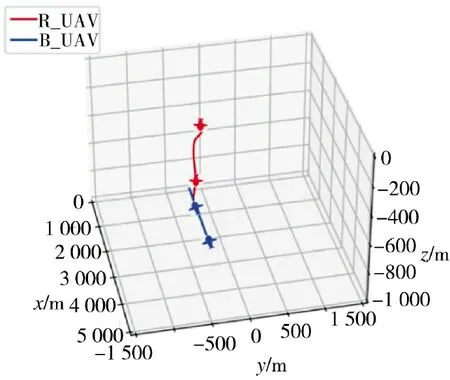
图9 蓝方飞行器初始位置（x2，y2，z2）=（5 000，-500，-500）Fig.9 The initial position of the blue aircraft（x2，y2，z2）=（5 000，-500，-500）

图10 蓝方飞行器初始位置（x2，y2，z2）=（5 000，500，-500）Fig.10 The initial position of the blue aircraft（x2，y2，z2）=（5 000，500，-500）

图11 蓝方飞行器初始位置（x2，y2，z2）=（5 000，-500，-250）Fig.11 The initial position of the blue aircraft（x2，y2，z2）=（5 000，-500，-250）

可以看到，针对不同位置出发的蓝方飞行器，红方飞行器都可以实施追踪打击，算法的普适性强，能够适用于多种环境。

4 结论

本文以固定翼飞行器突防拦截为背景，兼顾工程研制的基本约束和预先研究的前沿性，选取速度快、续航能力强、能适用于多种场景的固定翼飞行器为研究对象，围绕固定翼飞行器控制模型设计、基于深度强化学习的固定翼飞行器自主决策方法展开研究。根据现有固定翼飞行器参数，结合运动学与动力学方程完成对飞行器姿态控制的建模。并基于DDPG 算法，设计固定翼飞行器动态控制方法，通过对状态空间、动作空间和奖励函数的设计，使得飞行器的决策过程中符合现实战场环境。在仿真环境下，利用大量数据和数据驱动的方法，让深度强化学习控制的固定翼飞行器在二维和三维空间中与敌机进行博弈对抗。由深度强化学习控制的固定翼飞行器在二维和三维空间下分别与敌机进行博弈对抗，取得了56.9%和28.6%的胜率。证明了大数据和数据驱动对于提升固定翼飞行器的控制能力和决策效果的有效性。

尽管本研究在固定翼飞行器控制领域取得了一定的成果，实现了基于DDPG 算法的固定翼无人机控制，但仍存在一些潜在的研究方向和待解决的问题。未来的研究将重点关注以下几个方面：首先，算法拓展方向将尝试引入更多种深度强化学习算法，如PPO 和TD3 等，以比较它们对实验结果的影响。其次，算法优化方向将着眼于调整超参数和网络架构以及奖励函数的设计，以提高模型的拟合能力，并考虑引入不同的噪声以扩展智能体的状态空间，以加速算法的收敛速度和提高性能稳定性。最后，环境拓展方向将考虑研究多智能体协同控制算法，以实现对多个固定翼无人机模型的控制，以探索固定翼飞行器在更广泛应用领域中的潜力。这些工作将进一步推动固定翼飞行器控制技术的发展和应用范围的扩大。