n值R0命题逻辑系统中公式的条件随机真度

许倩,惠小静,南琼

(延安大学数学与计算机科学学院, 陕西 延安 716000)

0 引言

众所周知,数理逻辑中引入概率方法的思想,从20世纪70年代就已经开始逐渐兴起,目前已经有“概率逻辑学”的专著出版,并且基于真度的多种逻辑系统的程度化研究也被广泛开展,比如文献[1]中在多值逻辑系统中提出公式的μ-真度理论,文献[2-3]在ukasiweicz命题逻辑中分别提出公式的真度理论和极限定理和Γ-真度理论和极限定理,但是真度理论的研究仍存在一些局限性,既缺乏前面提到的随机性,并且没有考虑前提条件。在此问题的基础上,文献[4-7]中将赋值集的随机化方法分别利用在经典命逻辑系统、三值R0命题逻辑系统、三值Gödel命题逻辑系统以及R0型n值和模糊逻辑系统中,提出了公式的随机真度概念并且建立了随机逻辑度量空间。文献[8-11]中又在条件概率的思想基础上,将条件真度概念以及相应的推理规则在经典命题逻辑系统、三值R0命题逻辑系统、n值ukasiewicz命题逻辑系统、R0型模糊命题逻辑系统中提出并阐明。在文献[12-20]的基础上,本研究基于条件概率的思想和n值R0命题系统的广义演绎定理的表现形式,为了刻画n值R0命题系统中一个命题在一定条件下的随机真度,在n值R0命题系统中提出了公式的条件随机真度,证明了条件随机真度MP规则和HS规则,建立了条件随机逻辑度量空间,为n值R0命题系统的条件随机发散度的概念的提出奠定基础。

1 预备知识

设S={p1,p2,…}为原子公式集,F(S)是S生成的(—,∨,→)型自由代数,则称F(S)中的元为公式,约定A⊗B=—(A→—B),A⊕B=—A→B,A2=A⊗A,Am+1=Am⊗A,A,B∈F(S)。

设n∈,n≥3,令在L中规定则L成为(—,∨,→)型代数,称为n值R0命题逻辑系统,记作

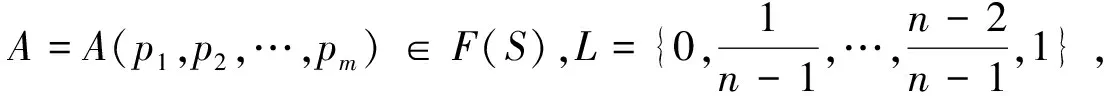
定义1.1[7]设={1,2,…}为自然数集,D=(D1,D2,…)为无穷向量序列,如果对∀i∈均有为n值非退化概率分布,要求且称D为n值概率分布序列。

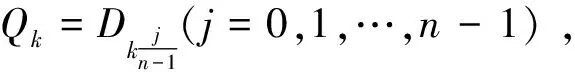
命题1.1[7]∑{φ(α):α=(x1,x2,…,xm)∈Lm}=1。

定义1.3[7]设D是n值概率分布序列,A=A(p1,p2,…,pm)∈F(S),令

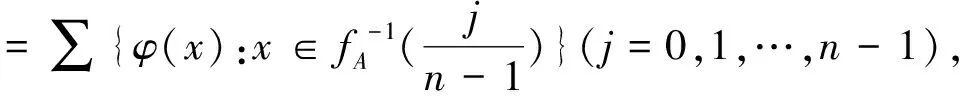
定理1.1[12]设Γ⊂F(S),A,B∈F(S),若Γ∪{A}├B,则Γ├A→B。

定理1.2[12](广义演绎定理) 设Γ是一理论,即Γ⊂F(S),A,B∈F(S),则在n值R0命题系统中广义演绎定理成立,即Γ∪{A}├B当且仅当Γ├A2→B。

命题1.2[7]设D是n值概率分布序列,A=A(p1,p2,…,pm)∈F(S),则公式A的随机真度可表示为

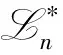
1)A⊗B→A,A⊗B→B;

2)A⊗B↔B⊗A。

命题1.4[12]设D是n值概率分布序列,A,B∈F(S),则:

2 公式的条件随机真度

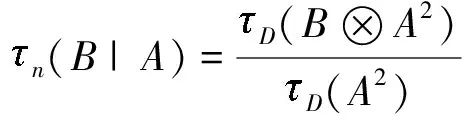
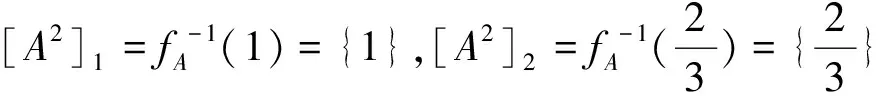
=0.2+0.2

=0.4.

又因为B⊗A2=(q1→q2)⊗q12=—((q1→q2)→—q12),则有

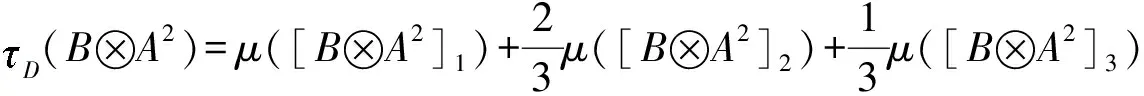
=0.06+0.04+0.2

=0.3.

可求解出条件随机真度:

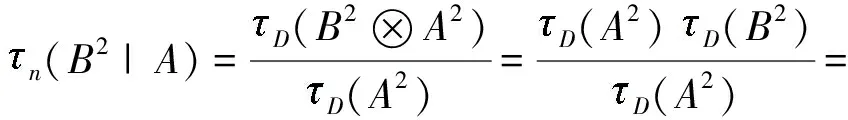
引理2.1∀a,b,c∈[0,1],c+b⊗c≥a⊗c+(a→b)⊗c。

引理2.1的证明若a≤b,则a→b=1,所以c+b⊗c≥a⊗c+1⊗c,因为fa(x)=x⊗a单调递增,所以a⊗c≤b⊗c,又因为1⊗c=c,所以不等式成立;

若a>b,因为a→b=a′∨b,所以a⊗c+(a→b)⊗c=a⊗c+(a′∨b)⊗c:

1)当a′≤b时,a⊗c+(a→b)⊗c=a⊗c+(a′∨b)⊗c=a⊗c+b⊗c,又因为a⊗c≤1⊗c,则不等式成立。

2)当a′>b时,a⊗c+(a→b)⊗c=a⊗c+(a′∨b)⊗c=a⊗c+a′⊗c:

①当a>c≥b时,则a′c′时,a⊗c+a′⊗c=c+0=c,不等式成立;

②当a>b≥c时,则a′c′时,a⊗c+a′⊗c=c+0=c,不等式成立;

③当c>a>b时,则a′≥c′,当a≤c′时,a⊗c+a′⊗c=0+0=0,不等式成立;当a>c′时,a⊗c+a′⊗c=c+0=c,不等式成立。

综上所述,c+b⊗c≥a⊗c+(a→b)⊗c不等式成立。

定理2.2(条件随机真度推理规则)

3 条件随机度量空间

1)若A≈ΓB,则ξΓ(A,B)=1;

3)ξΓ(A,C)≥ξΓ(A,B)+ξΓ(B,C)-1。

定理3.1的证明1)若A≈ΓB,则A→B与B→A均为重言式,那么(A→B)∧(B→A)也为重言式,所以ξΓ(A,B)=1。

定理3.2ρΓ:F(S)×F(S)→[0,1]是F(S)上的条件随机伪距离,称(F(S),ρΓ)为条件随机度量空间。

2)ρΓ(—A,—B)=ρΓ(A,B);

4)～5)同3)可证得。

下面进一步给出在F(S)中基于信息Γ的近似推理理论。

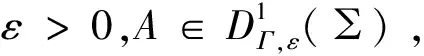
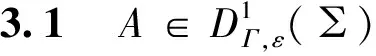
推论3.1的证明由定义3.2可证得结论。

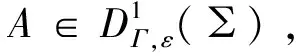
ρΓ(A,D(∑))=inf{ρΓ(A,B)|B∈D(∑)}=inf{1-ξΓ(A,B)|B∈D(∑)}

=1-sup{ξΓ(A,B)|B∈D(∑)}.

并且由定义3.1可得

得证。

4 结束语

利用随机化映射和条件概率方法,在n值R0命题系统中提出了公式的条件随机真度,并证明了条件随机真度的MP规则和HS规则,建立了条件随机逻辑度量空间,最后进一步给出了在条件Γ下的近似推理理论。