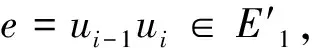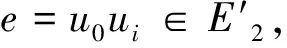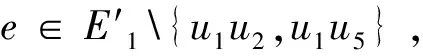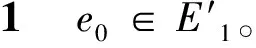两类联图的PI不变边

熊金,李怡博

(湖北大学数学与统计学学院, 湖北 武汉 430062)

0 引言

设G=(V(G),E(G))和H=(V(H),E(H))是两个图。G和H的联图,记为G∨H,定义为:

V(G∨H):=V(G)∪V(H),

E(G∨H):=E(G)∪E(H)∪{uv|u∈V(G),v∈V(H)}.

设G1,G2,…,Gr是r个点不交的连通图,我们用G1+G2+…+Gr表示G1,G2,…,Gr的不交并图。若G1=G2=…=Gr,则记G1+G2+…+Gr=rG。

令Sk,r=Kk∨rK1,Wn=Cn∨K1,其中Kk为k阶完全图,Cn为n阶圈。Sk,r和Wn分别称为门槛图[1]和轮图。

设G=(V(G),E(G))是一个简单连通图。令x,y∈V(G),e=uv∈E(G)。图G中x和y的距离,记为dG(x,y),定义为x与y的最短路的长。令

N1(e|G)={x∈V(G)|dG(x,u)

N2(e|G)={y∈V(G)|dG(y,u)>dG(y,v)}.

图G的Padmakar-Ivan指标,简记为PI指标,定义为:

PI(G)=∑e=uv∈E(G)[n1(e|G)+n2(e|G)],

其中ni(e|G)=|Ni(e|G)|,i=1,2。

如果PI(G-e)=PI(G),那么边e称为图G的PI不变边。

图的PI指标是Khadikar[4]在2000年提出的一个基于距离的拓扑指标。PI指标被提出以来,受到了广大学者的关注,广泛应用于QSAR和QSPR领域,得到了一些研究成果[2-4]。Khalifeh等[5]给出了笛卡尔乘积图的PI指标的精确表达式。最近, Indulal等[6]证明了含有奇圈的图G存在PI不变边,其中奇圈的每条边都是图G的PI不变边,并且证明了当n≥4时,完全图Kn没有PI不变边。本文中,我们分别研究门槛图和轮图存在PI不变边的条件。

1 门槛图的PI指标及不变边

本节中,我们主要研究门槛图Sk,r的PI指标和Sk,r存在PI不变边的条件。

首先给出n阶完全图Kn的PI指标。

定理1.1当n≥2时,PI(Kn)=n2-n。

定理1.1的证明当n=2时,设e=uv∈E(K2),显然N1(e|K2)={u},N2(e|K2)={v}。于是n1(e|K2)+n2(e|K2)=2。

当n≥3时,对任意的边e=uv∈E(Kn)及任意的点w∈V(Kn){u,v},均有dKn(w,u)=dKn(w,v)。因此N1(e|Kn)={u},N2(e|Kn)={v}。

于是n1(e|Kn)+n2(e|Kn)=2。

接下来,我们计算PI(Sk,r)的值。

定理1.2设k,r是正整数,则PI(Sk,r)=kr2+kr+k2-k。

定理1.2的证明设e=vivj∈E(Sk,r),vl∈V(Sk,r){vi,vj}。

首先证明下面的论断。

论断11)如果e∈E1,那么n1(e|Sk,r)+n2(e|Sk,r)=2;

2)如果e∈E2,那么n1(e|Sk,r)+n2(e|Sk,r)=r+1。

论断1的证明1)注意到dSk,r(vl,vi)=dSk,r(vl,vj)=1。

于是N1(e|Sk,r)={vi},N2(e|Sk,r)={vj}。因此n1(e|Sk,r)+n2(e|Sk,r)=2。

2)若vl∈V1,则dSk,r(vl,vi)=dSk,r(vl,vj)=1;若vl∈V2,则dSk,r(vl,vi)=1<2=dSk,r(vl,vj)。因此N1(e|Sk,r)={vi}∪(V2{vj}),N2(e|Sk,r)={vj}。于是n1(e|Sk,r)+n2(e|Sk,r)=r+1。

由论断1可知,

=2|E1|+(r+1)|E2|

=kr2+kr+k2-k.

定理1.3如果r=k-1,那么E2的每一条边都是Sk,r的PI不变边。

定理1.3的证明设G=Sk,r-v1vk+1, 则dG(v1,vk+1)=2。令E11={v1vj|2≤j≤k},E21={v1vj|k+2≤j≤k+r},E22={vivk+1|2≤i≤k}。显然E11⊂E1,E21⊂E2,E22⊂E2,且|E11|=k-1,|E21|=r-1,|E22|=k-1。

我们首先证明下面的论断。

论断21)如果e∈E11,那么n1(e|G)+n2(e|G)=3;

2)如果e∈E1E11,那么n1(e|G)+n2(e|G)=2;

3)如果e∈E21,那么n1(e|G)+n2(e|G)=r;

4)如果e∈E22,那么n1(e|G)+n2(e|G)=r+2;

5)如果e∈E2(E21∪E22),那么n1(e|G)+n2(e|G)=r+1。

论断2的证明1)令e=v1vj,其中2≤j≤k。易知dG(vk+1,v1)=2>1=dG(vk+1,vj),且对任意vs∈V(G){v1,vj,vk+1},均有dG(vs,v1)=dG(vs,vj)=1。因此N1(e|G)={v1},N2(e|G)={vj,vk+1}。于是n1(e|G)+n2(e|G)=3。

2)令e=vivj,其中2≤i

3)令e=v1vj,其中k+2≤j≤k+r。当vs∈{vk+1}∪V1{v1}时,dG(vs,v1)=dG(vs,vj);当vs∈V2{vk+1,vj}时,有dG(vs,v1)=1<2=dG(vs,vj)。于是N1(e|G)={v1}∪(V2{vk+1,vj}),N2(e|G)={vj}。因而n1(e|G)+n2(e|G)=r。

4)令e=vivk+1,其中2≤i≤k。若vs∈V1{v1,vi},则dG(vs,vi)=dG(vs,vk+1)=1;若vs∈{v1}∪(V2{vk+1}),有dG(vs,vi)=1<2=dG(vs,vk+1)。因此N1(e|G)={v1,vi}∪(V2{vk+1}),N2(e|G)={vk+1}。

于是n1(e|G)+n2(e|G)=r+2。

5)令e=vivj,其中2≤i≤k,k+2≤j≤k+r。如果vs∈V1{vi},那么dG(vs,vi)=dG(vs,vj)=1;如果vs∈V2{vj},那么dG(vs,vi)=1<2=dG(vs,vj)。于是N1(e|G)={vi}∪(V2{vj}),N2(e|G)={vj}。

因此n1(e|G)+n2(e|G)=r+1。

由论断2可知,

=3|E11|+2(|E1|-|E11|)+r|E21|+(r+2)|E22|

+(r+1)(|E2|-|E21|-|E22|-1)

=kr2+(k-2)r+k2+k-2,

进而,根据定理1.2可得,PI(Sk,r)-PI(G)=2r-2k+2。因此,当r=k-1时,PI(Sk,r)-PI(G)=0,即v1vk+1是Sk,r的PI不变边。

由对称性,可知E2的每一条边都是Sk,r的PI不变边。

2 轮图的PI指标及不变边

本节中,我们主要研究轮图Wn的PI指标和Wn存在PI不变边的条件。

引理2.1[5]当n≥4时,Kn没有PI不变边。

我们先计算PI(Wn)的值。

定理2.2当n≥4时,PI(Wn)=n2+3n。

定理2.2的证明我们首先证明下面的论断。

论断3的证明1)注意到

dWn(ui-1,ui)=1<2=dWn(ui-1,ui+1);

dWn(ui+2,ui)=2>1=dWn(ui+2,ui+1)。

若us∈V(Wn){ui-1,ui,ui+1,ui+2},则dWn(us,ui)=dWn(us,ui+1)。于是N1(e|Wn)={ui-1,ui},N2(e|Wn)={ui+1,ui+2}。因此n1(e|Wn)+n2(e|Wn)=4。

2)若us∈{ui-1,ui+1},则dWn(us,ui)=dWn(us,u0);当us∈V(Wn){ui-1,ui,ui+1,u0}时,均有dWn(us,ui)=2>1=dWn(us,u0)。因此N1(e|Wn)={ui},N2(e|Wn)=V(Wn){ui-1,ui,ui+1}。从而n1(e|Wn)+n2(e|Wn)=n-1。

由论断3可知,

=n2+3n。

注意到W3≅K4,由引理2.1可知,W3没有PI不变边。

定理2.3对任意的1≤i≤4,uiu0均是W4的PI不变边。

定理2.3的证明令F=W4-u1u0。我们首先证明下面的论断。

论断41)如果e∈{u1u2,u1u4},那么n1(e|F)+n2(e|F)=5;

2)如果e∈{u2u3,u3u4,u2u0,u4u0},那么n1(e|F)+n2(e|F)=4;

3)如果e=u3u0,那么n1(e|F)+n2(e|F)=2。

论断4的证明1)令e=u1uj,其中j=2,4。易知dF(u1,uj)=1,dF(u2,u4)=2,且当ut∈{u3,u0}时,有dF(ut,u1)=2>1=dF(ut,uj)。于是N1(e|F)={u1,u6-j},N2(e|F)={u0,u3,uj}。因此n1(e|F)+n2(e|F)=5。

2)令e=uiuj,其中i=0,3,j=2,4。注意到dF(ui,uj)=dF(u0,u3)=1;dF(u2,u4)=2;dF(u1,ui)=2>1=dF(u1,uj)。于是N1(e|F)={ui,u6-j},N2(e|F)={u1,uj}。因而n1(e|F)+n2(e|F)=4。

3)对任意的ut∈{u1,u2,u4},有dF(ut,u3)=dF(ut,u0)。因此N1(e|F)={u3},N2(e|F)={u0}。于是n1(e|F)+n2(e|F)=2。

由论断4可知,

=5×2+4×4+2

=28,

从而,根据定理2.2可得,PI(W4)=42+3×4=28=PI(F), 故u1u0是W4的PI不变边。

由对称性可知,对任意的1≤i≤4,uiu0都是W4的PI不变边。

引理2.4对任意的1≤i≤5,uiu0均不是W5的PI不变边。

引理2.4的证明令H=W5-u1u0。我们先证明下面的论断。

论断51)如果e∈{u1u2,u1u5,u2u0,u5u0},那么n1(e|H)+n2(e|H)=5;

3)如果e∈{u3u0,u4u0},那么n1(e|H)+n2(e|H)=3。

论断5的证明1)令e=u1uj,其中j=2,5。易知dH(uj,u1)=1,dH(u2,u5)=2及dH(u7-k,u1)=dH(u7-k,uj)=2,其中|k-j|=1且k≠1;当up∈{uk,u0}时,有dH(up,u1)=2>1=dH(up,uj)。因此N1(e|H)={u1,u7-j},N2(e|H)={u0,uj,uk}。

于是n1(e|H)+n2(e|H)=5。

令e=u0uj,其中j=2,5。注意到dH(u1,u0)=2>1=dH(u1,uj)及dH(uk,u0)=dH(uk,uj)=1,其中|k-j|=1且k≠1;对任意的up∈{u7-j,u7-k},均有dH(up,u0)=1<2=dH(up,uj)。因此N1(e|H)={u0,u7-j,u7-k},N2(e|H)={u1,uj}。从而n1(e|H)+n2(e|H)=5。

2)令e=uiui+1,其中2≤i≤4。注意到dH(ui-1,ui)=1<2=dH(ui-1,ui+1);dH(ui+2,ui)=2>1=dH(ui+2,ui+1); 若up∈{ui+3,u0},则dH(up,ui)=dH(up,ui+1)。于是N1(e|H)={ui-1,ui},N2(e|H)={ui+1,ui+2}。

因此n1(e|H)+n2(e|H)=4。

3)令e=u0uj,其中j=3,4。易知dH(u0,uj)=dH(u3,u4)=1及dH(uk,u0)=1<2=dH(uk,uj),其中|k-j|=2且k≠1; 对任意的up∈{u1,u7-k,u7-j},有dH(up,u0)=dH(up,uj)。于是N1(e|H)={u0,uk},N2(e|H)={uj}。

因而n1(e|H)+n2(e|H)=3。

由论断5可知,

=5×4+4×3+3×2

=38,

进而,根据定理2.2可得,PI(W5)-PI(H)=52+3×5-38=2。因此,u1u0不是W5的PI不变边。

由对称性可知,对任意的1≤i≤5,uiu0均不是W5的PI不变边。

定理2.5当n≥5时,Wn没有PI不变边。

定理2.5的证明令Q=Wn-e0,e0∈E(Wn)。考虑如下的两种情形:

由对称性,不妨假设e0=u1u2。我们先证明下面的论断。

论断61)如果e∈{u2u3,u1un},那么n1(e|Q)+n2(e|Q)=3;

3)如果e∈{u1u0,u2u0},那么n1(e|Q)+n2(e|Q)=n;

论断6的证明1)令e=u2u3。注意到dQ(u4,u2)=2>1=dQ(u4,u3),且当ul∈V(Q){u2,u3,u4}时,有dQ(ul,u2)=dQ(ul,u3)。因此N1(e|Q)={u2},N2(e|Q)={u3,u4}。于是n1(e|Q)+n2(e|Q)=3。

令e=u1un。易知dQ(un-1,u1)=2>1=dQ(un-1,un),且若ul∈V(Q){u1,un,un-1},则dQ(ul,u1)=dQ(ul,un)。于是N1(e|Q)={u1},N2(e|Q)={un-1,un}。从而n1(e|Q)+n2(e|Q)=3。 2)令e=uiui+1,其中3≤i≤n-1。易见dQ(ui-1,ui)dQ(ui+2,ui+1);如果ul∈V(Q){ui-1,ui,ui+1,ui+2},那么dQ(ul,ui)=dQ(ul,ui+1)。因此N1(e|Q)={ui-1,ui},N2(e|Q)={ui+1,ui+2}。于是n1(e|Q)+n2(e|Q)=4。

3)令e=u1u0。注意到dQ(un,u1)=dQ(un,u0)=1; 如果ul∈V(Q){u1,un},那么dQ(ul,u1)>dQ(ul,u0)。因此N1(e|Q)={u1},N2(e|Q)=V(Q){u1,un}。从而n1(e|Q)+n2(e|Q)=n。

令e=u2u0。易知dQ(u3,u2)=dQ(u3,u0)=1;对任意的ul∈V(Q){u2,u3},均有dQ(ul,u2)>dQ(ul,u0)。于是N1(e|Q)={u2},N2(e|Q)=V(Q){u2,u3}。因而n1(e|Q)+n2(e|Q)=n。

4)令e=uiu0,其中3≤i≤n。当ul∈{ui-1,ui+1}时,有dQ(ul,ui)=dQ(ul,u0);当ul∈V(Q){ui-1,ui,ui+1}时,有dQ(ul,ui)>dQ(ul,u0)。于是N1(e|Q)={ui},N2(e|Q)=V(Q){ui-1,ui,ui+1}。因此n1(e|Q)+n2(e|Q)=n-1。

由论断6可知,

=3×2+4×(n-3)+n×2+(n-1)×(n-2)

=n2+3n-4,

从而,根据定理2.2可得,PI(Wn)-PI(Q)=n2+3n-(n2+3n-4)=4。

因此,u1u2不是Wn的PI不变边。

根据对称性,不妨假设e0=u1u0。由引理2.4,我们有n≥6。我们先证明下面的论断。

论断71)如果e∈{u1u2,u1un,u2u0,unu0},那么n1(e|Q)+n2(e|Q)=n;

2)如果e∈{u3u4,un-2un-1},那么n1(e|Q)+n2(e|Q)=5;

4)如果e∈{u3u0,un-1u0},那么n1(e|Q)+n2(e|Q)=n-2;

论断7的证明1)令e=u1u2。注意到dQ(un-1,u1)=dQ(un-1,u2)=2;dQ(un,u1)=1<2=dQ(un,u2);若uq∈V(Q){u1,un-1,un},则dQ(uq,u1)>dQ(uq,u2)。因此N1(e|Q)={u1,un},N2(e|Q)=V(Q){u1,un-1,un}。

于是n1(e|Q)+n2(e|Q)=n。

令e=u1un。易见dQ(u3,u1)=dQ(u3,un)=2;dQ(u2,u1)=1<2=dQ(u2,un);如果uq∈V(Q){u1,u2,u3},则dQ(uq,u1)>dQ(uq,un)。因此N1(e|Q)={u1,u2},N2(e|Q)=V(Q){u1,u2,u3}。从而n1(e|Q)+n2(e|Q)=n。

令e=u2u0。注意到dQ(u3,u2)=dQ(u3,u0)=1;dQ(u1,u2)=1<2=dQ(u1,u0);当uq∈V(Q){u1,u2,u3}时,有dQ(uq,u2)>dQ(uq,u0)。于是N1(e|Q)={u1,u2},N2(e|Q)=V(Q){u1,u2,u3}。

因此n1(e|Q)+n2(e|Q)=n。

令e=unu0。易知dQ(un-1,un)=dQ(un-1,u0)=1;dQ(u1,un)=1<2=dQ(u1,u0);对任意的uq∈V(Q){u1,un-1,un},均有dQ(uq,un)>dQ(uq,u0)。于是N1(e|Q)={u1,un},N2(e|Q)=V(Q){u1,un-1,un}。

因而n1(e|Q)+n2(e|Q)=n。

2)令e=u3u4。易知dQ(u5,u3)=2>1=dQ(u5,u4);若uq∈{u1,u2},则dQ(uq,u3)

于是n1(e|Q)+n2(e|Q)=5。

令e=un-2un-1。注意到dQ(un-3,un-2)=1<2=dQ(un-3,un-1);当uq∈{u1,un}时,有dQ(uq,un-2)>dQ(uq,un-1);对任意的uq∈V(Q){u1,un-3,un-2,un-1,un},有dQ(uq,un-2)=dQ(uq,un-1)。于是N1(e|Q)={un-2,un-3},N2(e|Q)={u1,un-1,un}。

因此n1(e|Q)+n2(e|Q)=5。

3)令e=uiui+1,其中2≤i≤n-1且i≠3,n-2。

易见dQ(ui-1,ui)=1<2=dQ(ui-1,ui+1);dQ(ui+2,ui)=2>1=dQ(ui+2,ui+1);当uq∈V(Q){ui-1,ui,ui+1,ui+2}时,均有dQ(uq,ui)=dQ(uq,ui+1)。因此N1(e|Q)={ui-1,ui},N2(e|Q)={ui+1,ui+2}。

从而n1(e|Q)+n2(e|Q)=4。

4)令e=u3u0。如果uq∈{u1,u2,u4},那么dQ(uq,u3)=dQ(uq,u0);当uq∈V(Q){u1,u2,u3,u4}时,均有dQ(uq,u3)>dQ(uq,u0)。因此N1(e|Q)={u3},N2(e|Q)=V(Q){u1,u2,u3,u4}。

于是n1(e|Q)+n2(e|Q)=n-2。

令e=un-1u0。若uq∈{u1,un-2,un},则dQ(uq,un-1)=dQ(uq,u0);对任意的uq∈V(Q){u1,un-2,un-1,un},有dQ(uq,un-1)>dQ(uq,u0)。于是N1(e|Q)={un-1},N2(e|Q)=V(Q){u1,un-2,un-1,un}。

因而n1(e|Q)+n2(e|Q)=n-2。

5)令e=uiu0,其中4≤i≤n-2。当uq∈{ui-1,ui+1}时,有dQ(uq,ui)=dQ(uq,u0);对任意uq∈V(Q){ui-1,ui,ui+1},均有dQ(uq,ui)>dQ(uq,u0)。于是N1(e|Q)={ui},N2(e|Q)=V(Q){ui-1,ui,ui+1}。

因此n1(e|Q)+n2(e|Q)=n-1。

由论断7可知,

=n×4+5×2+4×(n-4)+(n-2)×2+(n-1)×(n-5)

=n2+4n-5,

进而,根据定理2.2可得,PI(Wn)-PI(Q)=n2+3n-(n2+4n-5)=5-n。故当n≥6时,PI(Wn)-PI(Q)<0,即u1u0不是Wn的PI不变边。