“指对混搭函数不等式的证明”教学设计与思考
湖北省武汉市黄陂区第一中学盘龙校区 (430312) 卢 珍 李红春
1.问题提出
函数导数综合问题是高考的热点和难点,不少高三教师面对这块内容的复习常常老生常谈,缺乏自己深入的见解,课后再辅以“题海战术”,展现的是大题量,快节奏,机械重复的教学形态,因此学生对所学的内容兴趣不高,解题停留于模仿,对问题的本源不明,解题无序,推论无理.为了提升教师的思想认识,不断优化教学行为,前不久,笔者执教了一节题为《指对混搭函数不等式的证明》的展示课,获得了听课老师的充分好评.本文将这节课的教学设计和教学思考呈现出来,供分享.
2.教学设计展示
2.1 教学目标
(1)能从“阶”的角度分析分式型函数的极值;
(2)体会“分而治之”法解决问题的要领,并能用它证明一些常见指对混搭函数不等式;
(3)更加深刻体会到数学学习中“重视基础,回归基本”的价值.
2.2 教学重难点
教学重点:用“分而治之”法证明指对混搭函数不等式.
教学难点:灵活对函数不等式进行变形.
2.3 教学过程
本节课为借班授课,授课班级为某省级示范学校学生,学生基础较好,课前老师已将如下问题1让学生提前进行了思考.
问题1 (2020年山东卷改编)求证2ex-1-lnx>1+ln2.
(1)问题铺垫
课堂开始,教师巡查课堂,找到了三种不同的解法,并让学生代表用投影仪展示出来.


解法2:原不等式变形为eln2+x-1-(ln2+x-1)-1+x-lnx-1>0,故只需证[eln2+x-1-(ln2+x-1)-1]+(elnx-lnx-1)>0.设g(x)=ex-x-1,显然g(x)≥0在R上恒成立,于是g(ln2+x-1)+g(lnx)≥0,而等号取不到,故g(ln2+x-1)+g(lnx)>0,即[eln2+x-1-(ln2+x-1)-1]+(elnx-lnx-1)>0,故原不等式成立.
解法3:原不等式等价为2ex-1-1>ln(2x),由切线不等式ex≥x+1知ex-1≥x,于是2ex-1≥2x,lnx≤x-1,又由lnx≤x-1得ln(2x)≤2x-1,于是2ex-1-1≥2x-1≥ln(2x),两处取等条件不一致,故2ex-1-1>ln(2x),原不等式成立.
教师:解法1是将函数不等式f(x)>g(x)的证明等价为(f(x)-g(x))min>0来处理,进而将问题转化求函数的最值,这是一种常见处理问题的方法;解法2借助同构,利用熟悉函数的有界性求解,过程简单;解法3借助熟悉的结论ex≥x+1和lnx≤x-1,直接构建不等关系,直观简捷,体现着较高的数学素养.下面将上述试题变式成如下问题,让学生再思考:
问题2 求证:2ex-2>xlnx.
设计意图:通过2020年山东高考改编试题的引入,集思广益,总结回顾了处理这类问题学生接触过的三种基本方法.借助问题变式,学生思维受挫,激发学生的求知欲.
(2)观察发现
观察以下六个函数的图像(如图1),回答问题.

图1

问题4 根据问题3的结论,结合下列函数的特点,猜想下列函数是否有最值,有怎样的最值,并求导验证你的猜想:
学生分成四个小组,分别验算猜想,此时教师用几何画板展示四个函数图像(如图2):

图2
设计意图:从学生较为熟悉的“六大函数”图像入手,引导其从“阶”的角度归纳出“高阶比低阶”和“低阶比高阶”函数取极值的规律,再借助一些具体函数,让学生经历分析猜想,求导验证,直观感受,体会规律存在的一般性,为后续求解问题做好铺垫.
(3)数学应用
教师:数学问题的求解一般遵循等价转化,如将f(x)>0⟺f(x)min>0;利用充分性证明问题也是一种常见的方法,如将不等式f(x)>0先变形为m(x)>n(x),再证明m(x)min>n(x)max.利用这一思路,我们再来看问题2.


设计意图:通过对开头变式问题的解法分析,让学生充分领略到“分而治之”法处理问题的简便,借助思维过程的展示,让学生能知其然,更知其所以然.
(4)数学实践
问题5观察下列待证不等式,若用“分而治之法”证明,该如何变形,说出你的理由.

问题6下面是一道高考真题,请研读解答过程,分析用到的知识和方法,谈谈对你有哪些启发?

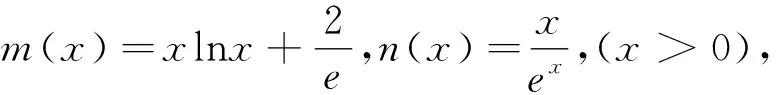


设计意图:分而治之法解题的重点不在计算,而在于学生动笔时,能准确判断如何将函数式分开,以及不等式两边变形的度.问题5对学生的考查力求“好钢用在刀刃上”.问题6是高考压轴题,让学生在课堂有限时间完成,难度颇大,设计为“阅读与反思”,更接地气.高考试题具有导向性,学习考试中心给出的参考答案就是在和命题专家直接对话,领悟试题解法背后的意图,对于学生改进学习方法很有意义.
(5)数学创新
问题7结合本节课学习的内容,立足函数的阶,从函数最值的角度出发,能否命制一道“指对混搭函数不等式”的证明题,并和大家分享你的命题思路.
设计意图:这一课堂环节的设置具有开放性,旨在培养学生的创新思维,借助从解题到命题的引导,将学生的思维引向深入,让学生不但会做别人命的题,更要善于自己提出问题.
(6)课堂小结及课后巩固(略)
3 教学反思
围绕这节课的教学设计,结合评委的意见,笔者觉得有如下几个亮点可供探讨.
3.1 适当铺垫,展现数学课堂教学的智慧
裴光亚老师曾经说过:教学艺术的基本特征是错位,为了抵达目标而偏离目标,其实不是偏离,而是营造目标赖以生存的环境,越是重要的东西,越是要隐藏起来,隐藏是为了展现诱惑[1].当学生们为课前给出的问题能“一题多解”,自我感觉良好时,老师接下来抛出的问题变式让他们一筹莫展,进退两难,在这样的情绪背景下,学生学习新方法的热情自然高涨.
3.2 用心设计,着力提升问题的针对性
问题是数学的心脏,本节课的难点在于引导学生对待证式进行合理变形,问题5设计为让学生观察待证不等式用“分而治之法”该如何去变形,重点考查学生变形方向的选择,显得独具匠心,如果设计为一般的证明题,求导计算的繁琐必将冲淡主题.问题7的设置具有相当的开放性,直接指向考查学生的创新思维,引导学生去探究和发现.
3.3 优化学法,于润物细无声处指导
“授人以鱼不如授人以渔”,教师在传授学生知识的同时,更要教给学生科学的学习方法.正如同教材,既蕴含了丰富的数学知识,更体现了研究问题的方法.我们一直强调学习要重视基础,回归基本,这就需要从复杂的情境中看到基本元素,从几何中看到基本图形,从代数中看到基本公式,从三角中看到基本变换,从统计中看到基本模型.如何做到这点,空洞的说教都不如让学生自己去体会.学生研读了问题6的参考答案,发现作为高考的压轴难题,却根基于这些学生耳熟能详的“基本函数”,倘若自己对这些“基本函数”的特征性质掌握得足够熟练,自然不会盲目变形.它带给学生的启示是:即使面对高考,夯实基础,回归基本绝不过时.
3.4 以身示范,教师树立了很好的榜样
《课程标准》中提出:要在数学教学中着力培养学生的创新精神和实践能力[2],优秀的教师是用教材而不是教教材.特别是高三复习阶段,教师要善于对知识进行整合与重构,对一些内容要有自己的独到见解.创新精神从何而来?教师首先要以身示范,成为学生心中乐于钻研问题的榜样;其次要留足时空,让学生放手去发现和创造.“分而治之”法求解指对混搭函数不等式的证明问题,平常解题中并不多见后,课堂上教师敢于选择这节内容来教学,源于教师的不断学习与钻研.在问题7的命题环节,更是留足时空,让学生将思维从课内引向课外,不断去探索和发现.

