一道课本例题变式探究教学之刍议

湖北省武汉市鲁巷中学 (430074) 熊 燕

一、原题再现

例题(人教版教材八年级上册P83第12题或九年级上册P63第10题)如图1,△ABD,△AEC都是等边三角形,求证:BE=CD.

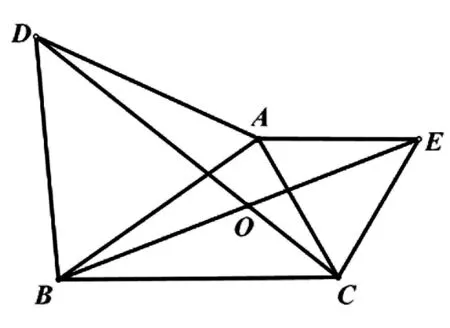
图1

分析:欲证BE=DE,可联想到△ADC与△ABE全等.对于△ADC≌△ABE的证明,可从两个角度分析:(1)从动态的角度来观察,把△ABE绕点A顺时针旋转60°,点B与点D,点E与点C重合,得到△ADC,所以△ADC≌△ABE.

(2)从静态的角度来分析,由题目“△ABD,△AEC都是等边三角形”的条件中可得到AD=AB,AC=∠BAE,且∠DAB=∠CAE=60°,再从∠DAB=∠CAE=60°这一条件进一步加工得出条件“∠DAC=∠BAE”,从而得到△ADC与△ABE全等(边角边).

点评:通过这样动与静两个角度的分析引导,培养学生分析问题的能力及几何直观能力,再把解题过程按条理顺序写出,提高了学生的逻辑思维推理能力,增强了学生的数学核心素养.

追问1:如图2,设CD与BE相交于点O,AB与CD相交于点M,AC与BE相交于点N.求∠BOD,∠DOE的度数.

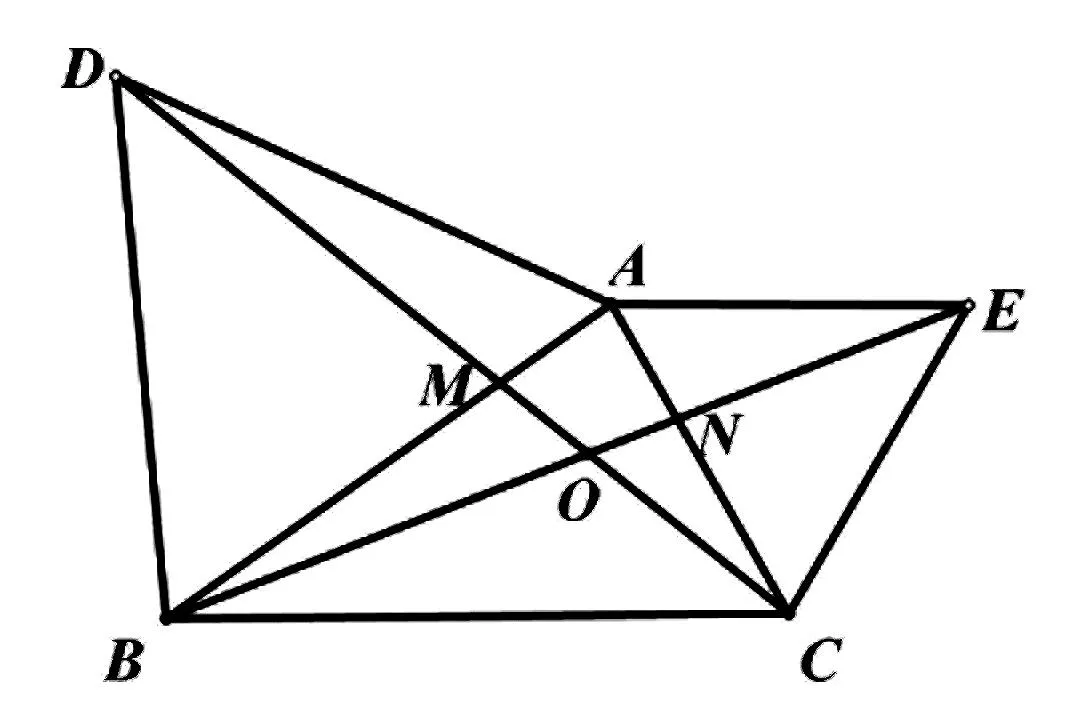
图2

分析:由原题的求证可得△ADC≌△ABE,则∠ADC=∠ABE,在线段AB与OD形成的“8”字型图形中,可得到∠DAB=∠BOD=60°,则∠DOE=120°;也可由∠DOE=∠BDO+∠DBO,从三角形全等得到角相等,即∠ADC=∠ABE,又∠BDO=60°-∠ADC,∠DBO=60°+∠ABE通过等量代换,进而得到∠DOE=120°.

点评:前者的解法建立在模型的基础上,后者的解法建立在等量代换基础上.

追问2:如图3,连接AO,其他条件不变.求证:AO平分∠DOE.

图3

分析:要证明AO平分∠DOE,可联想到角平分线的逆定理--到角的两边距离相等的点在角平分线上,因此,过点A分别作AG⊥CD,AH⊥BE,垂足分别是点G和点H.可通过再证明△ADG≌△ABH(或△AGC≌△AHE),得到AG=AH,从而证明AO平分∠DOE.当然,还可以由△ADC≌ABE,得到S△ADC≌S△AHE,且CD=BE,则AG=AH.

点评:不仅能通过证明三角形全等来证明AG=AH,还能通过等面积法来证明,让学生感受到面积法的美妙,体会数学的简洁美.

追问3:如图3,其他条件不变,求∠AOD,∠AOE,∠AOB,∠AOC,∠BOC的度数.

分析:综合上述追问1和追问2的相关结论,很自然地求得∠AOD=∠AOE=60°,∠AOB=∠AOC=∠BOC=120°.

点评:通对课本教材原题不懈地追问思考,得到许多结论;同时,对于追问1、追问2的多解思考,能进一步培养学生的发散思维能力,增强数学核心素养.

二、变式探究

变式1 已知△ABC中,每一个内角都小于120°,在△ABC内找一个点O,使∠AOB=∠AOC=∠BOC=120°.请画图找出点O,并证明.

分析:如图3,分别以AB,AC边为边向外作等边三角形△ABD,△AEC,连接CD,BE,则相交点即为要找的点O.此题的证明不难,实际上就是原题与追问3结论的应用.

点评:从逆向思考的角度,对原题的结论进行应用的变式.通对这样的变式,对原题与追问的结论进行进一步的理解并应用,培养学生的应用意识与创新意识.同时,该变式也可进一步拓展应用,点就是的费马点,这对学生后续进入高中学习平面向量知识奠定了基础,拓展了学生的数学视野.

变式2 如图4,以△ABC的三边为边在BC边的同一侧分别作三个等边三角形,即△ABD,△AEC,△BCF.请回答下列问题:

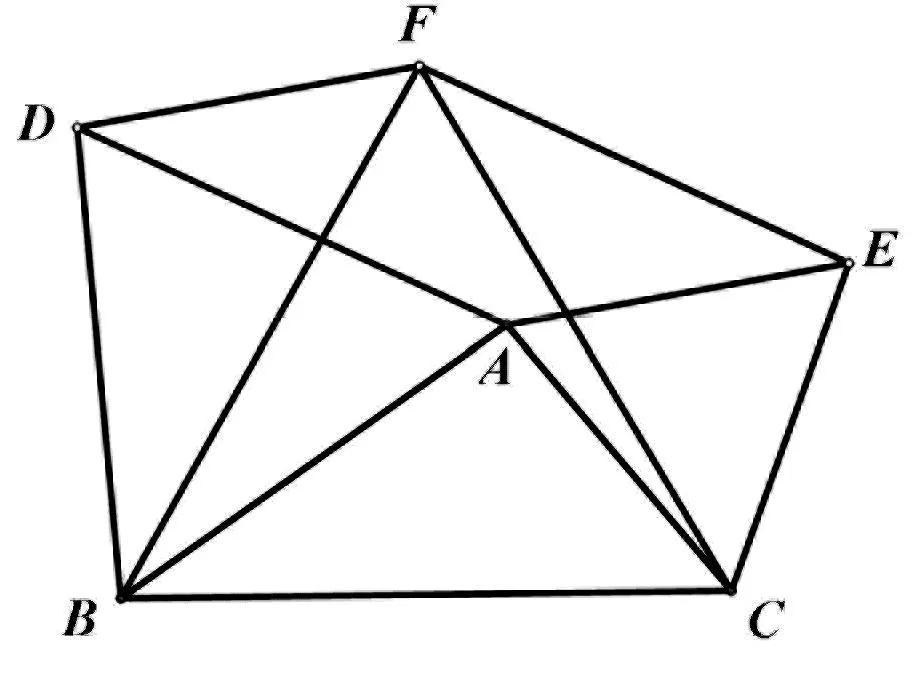
图4

(1)判断四边形ADFE是什么四边形?

(2)当△ABC满足什么条件时,四边形ADFE是菱形、矩形、正方形?

(3) 当满足什么条件时,以A,D,F,E为顶点的四边形不存在?

分析:(1)要证四边形ADFE是平行四边形,可通过两组对边分别相等来证明.

(2)当△ABC中的AB=AC时,则AD=AE,平行四边形ADFE是菱形.

当△ABC中的∠BAC=150°时,平行四边形ADFE是矩形.因为∠DAB=∠EAC=60°,∠BAC=150°,所以∠EAD=90°,所以平行四边形ADFE是矩形.由上述条件可得,当△ABC中的AB=AC,∠BAC=150°时,平行四边形ADFE是正方形;即同时满足是菱形与矩形的条件,则平行四边形ADFE是正方形.

(3)当△ABC中的∠BAC=60°时,以A,D,F,E为顶点的四边形不存在.因为∠CAB=∠BAD=∠EAC=60°,所以∠EAD=180°,此时A,D,E三点共线,四边形不存在.(也可用几何画板拖动点来验证.)

点评:从原题的角度进行拓展变式,即再以边向外作一个等边,从而产生出新的四边形,得出多个相关结论.通过这样的变式拓展,有利于提高学生的创新应用能力.

变式3 (人教版教材九年级上册P76第5题)如图5,△ABC和△ECD都是等边三角形,△EBC可以看作是△DAC经过平移、轴对称或旋转得到.说明得到△EBC的过程.

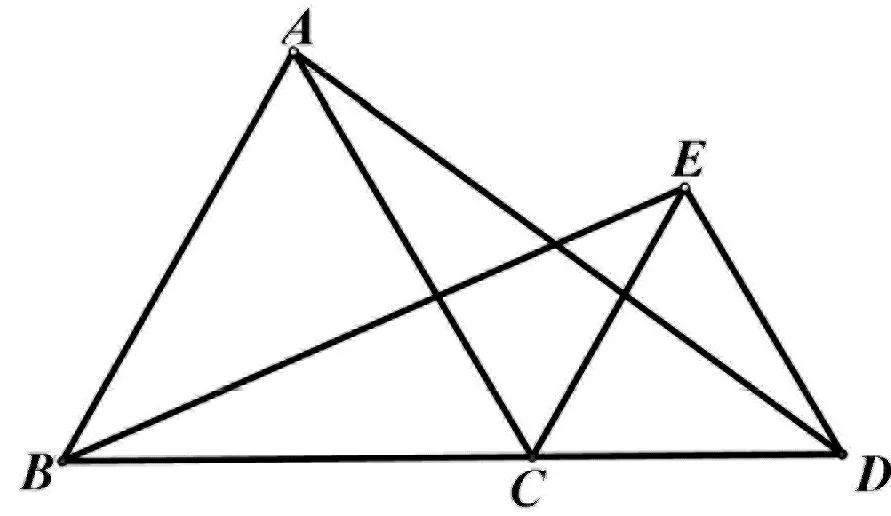
图5

分析:△EBC可以看作是△DAC绕点C逆时针旋转60°得到的.

追问1:如图6,设AD与EB相交于点O,AC与BE相交于点M,AD与CE相交于点N.求∠ACE,∠BOD的度数.

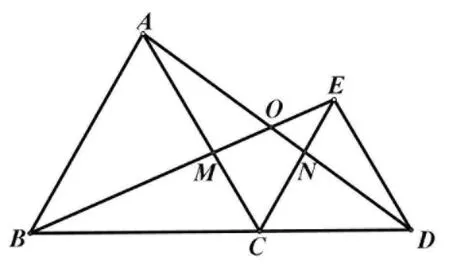
图6

分析:可类比前面原题的追问1,根据△ABC和△ECD都是等边三角形,所以∠ACB=∠ECD=60°,∠ACE=60°,由三角形全等或旋转性质可得∠CAD=∠CBE,在线段AC与OB形成的“8”字型图形中,可得到∠AOB=∠ACB=60°,则∠BOD=120°;也可由∠BOD=∠BAO+∠ABO,从三角形全等或旋转得到角相等,即∠CAD=∠CBE,又∠BAO=60°+∠CAD,∠ABO=60°-∠CBE,通过等量代换,进而得到∠BOD=120°.

追问2:如图7,连接CO,其他条件不变.求证:CO平分∠BOD.

图7

分析:可以类比前面原题的追问2,过点A分别作CG⊥AC,CH⊥CE,垂足分别是点G和点H.可通过再证明△BCG≌△ACH(△ECG≌△DCH或)得CG=CH,从而证明CO平分∠BOD.当然,也可以由△ACD≌△BCE得S△ACD=S△BCE,且AD=BE,则CG=CH.

追问3:如图8,若BD=10cm,点C是线段BD上的动点,分别以线段BC,CD边向上作等边三角形△ABC与△CDE,连接AE,点F是线段AE的中点.当点C从点B运动到点D时,求点F的运动路径长度是多少?

图8

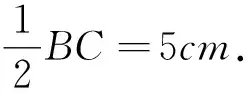
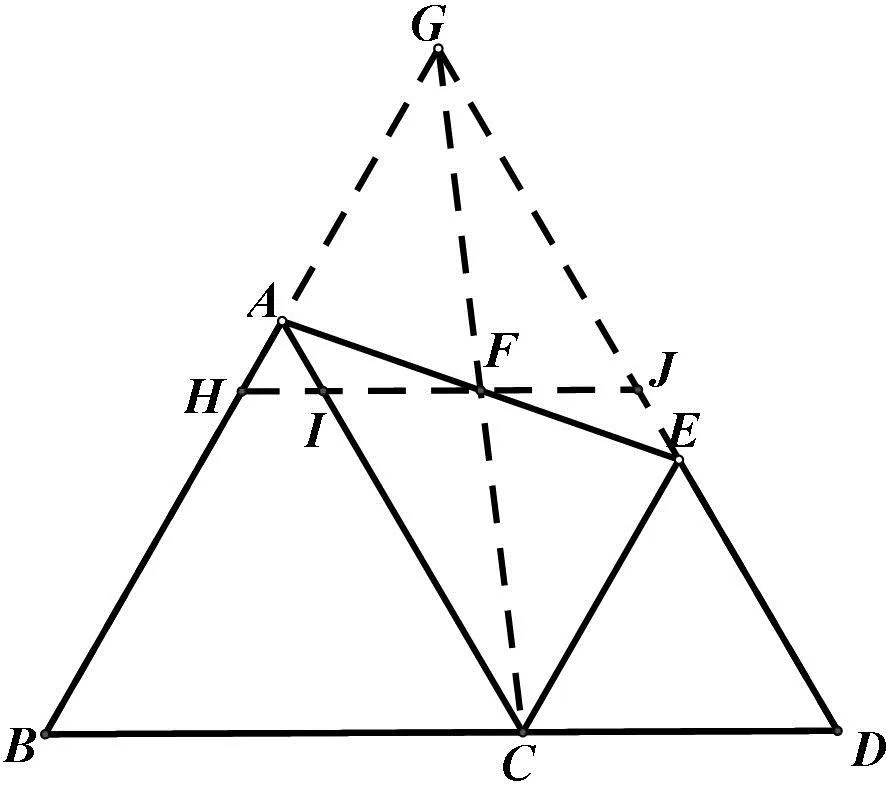
图9

另解:过点F作交FH∥BD交AB,AC,DG分别于点H,I,J,可证△AHI是等边三角形,四边形CIJD是平行四边形,设AB=a,由AF=FE可证△AFI≌△EFI,AI=EJ,设AB=a,AI=EJ=x,则DE=CD=IJ=10-a,CI=DJ=DE+EJ=10-a+x,所以AC=AI+CI=a,从而x=a-5,所以FH+FJ=HI+IJ=AI+CD=a-5+10-a=5.点F的运动路径长度是5cm.

点评:从特殊化的角度进行变式,追问1和追问2类比于原题的追问1和追问2,追问3拓展到动点问题.上述三道变式背景均来自对原题的再思考,通过这样的变式拓展,可培养学生的应用创新能力,在学生理解的情况下,注重变式思考的方向与模式,同时对其他题目的再思考起到借鉴作用.

三、题后反思

教材中的习题是解题的素材,要深入理解教材中习题,并引导学生深入分析,之后再进行解题的反思与归纳,从而提升学生的归纳能力.如:原题证明线段相等之后,可引导学生进行线段相等的证明方法的归纳.线段相等的证明方法总体可分为两种方法:第一,代数法,通过代数的计算,求出两线段的长度一样而相等(用勾股定理等),如原题的追问2中,通过面积相等从而求得线段相等;第二,几何法,通过几何证明得到线段相等,主要有三种方法:通过证明两个三角形全等,从而得到全等三角形的对应边相等,如原题的证明;通过等角对等边证明;特殊图形中的特殊线段相等,如平行四边形的对边相等,对角线互相平分等知识.

习题变式探究教学是促进有效数学学习的重要途径,通过对数学对象(数学概念、定理、公式等)从不同角度、不同层次、不同背景进行合理的变式探究,有意识地引导学生拾级而上,从“变”的现象中发现“不变”的本质,从“不变”中探求规律,从而深化对数学知识的理解,将特殊问题一般化,使零散知识规律化,改善学生对数学的认知结构,提高识别、应变、概括能力,达到学生能“发现问题、提出问题并解决问题”的目的,从而提高应用创新能力,提升学生的数学核心素养.