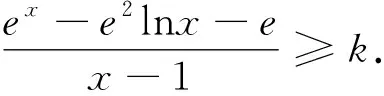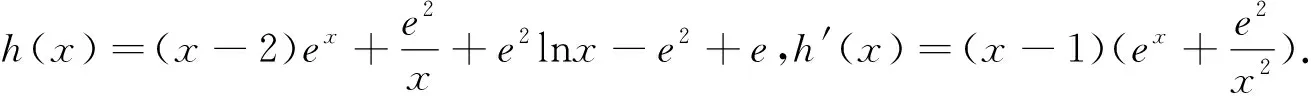基于命题角度谈一道导数题的命制过程*

安徽省砀山中学 (235300) 蔡 聪

笔者有幸参与了2022年宿州十三校高二下学期试卷的命制,感触颇深,现结合导数压轴题的命制过程与同仁分享.

一、试题呈现

已知函数f(x)=aex+blnx,曲线y=f(x)在(1,f(1))处的切线方程为y=(e-e2)x+e2.

(1)求a,b;(2)若f(x)≥kx-k+e,求k的值.

二、试题的构思过程

1.命题要求

因高二学生刚学习了导数的基本概念、四则运算及在单调性、极值与最值中的应用,未接触过多的题型,思考的深度不够,故设计时应控制难度.在选择考查方向时,笔者选择了从导数的几何意义、恒成立问题两个角度设计试题,尽量做到低起点,宽入口,深思考,符合《中国高考评价体系》的要求,切实考查学生的“四基”“四能”.

2.试题题源

分析:本题以指对混合型函数为对象,第一问考查导数的几何意义,较基础,第二问考查恒成立证明问题,学生可借助“指对分离”“凹凸反转”等技巧处理,意在考查学生的逻辑思维能力及分析问题、解决问题的能力.

3.改编考虑

保留题干,仍考查指对结合的函数形式,第二问的不等式证明题,学生易于着手,思路较多,常见的解题方法有:构造函数,分离参数,数形结合,凹凸反转等,利于考查学生分析问题,解决问题的能力,但怎样根据函数的特征选择合适的方法,是考验学生思维的很好着力点.笔者基于第二问做出改编,将证明问题转化为参数求值问题,区别于参数求范围,锻炼学生的应变能力.

4.方案设计过程

此过程中,笔者主要设置了四个题目,考查侧重点各有不同,现将前三个设计题目分享如下:

试题1已知函数f(x)=aex+blnx,曲线y=f(x)在(1,f(1))处的切线方程为y=(e-e2)x+e2.(1)求a,b; (2)证明:f(x)>0.

命题意图:试题以“隐零点”为技巧,考查函数的最值问题,难度较小.

试题3已知函数f(x)=aex+blnx,曲线y=f(x)在(1,f(1))处的切线方程为y=(e-e2)x+e2.(1)求a,b; (2)证明:f(x)≥(e-e2)x+e2.

命题意图:充分利用题目中的条件,构造证明型不等式,学生可移项构造函数解题,缺点是难度不够.

5.从学生角度的解法赏析

解:(数形结合)(1)易得a=1,b=-e2.

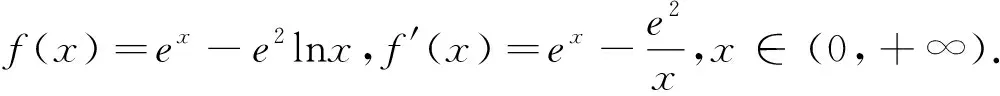
图1

评注:该法从数形结合的角度,联系直线过定点的问题,借助于切线的定义:割线的极限值,较容易得到k值,较直观但不够严谨.

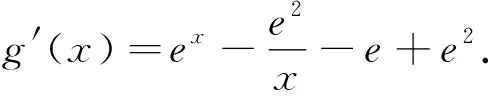
g′(1)=0知,当x∈(0,1)时,g′(x)<0,g(x)单调递减;当x∈(1,+∞)时,g′(x)>0,g(x)单调递增.g(x)≥g(1)=0.故k=e-e2满足条件.

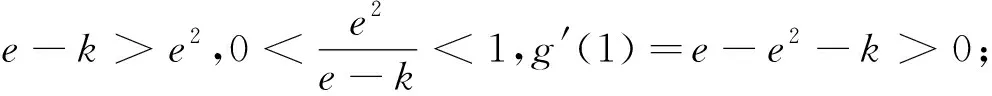
③当k>e-e2时,e2+k>e,ln(e2+k)>1,g′(1)=e-e2-k<0;当x>ln(e2+k)时,g′(x)>ex-e2-k>0,故存在x0∈(1,+∞),使g′(x0)=0.且x∈(1,x0)时,g′(x)<0,g(x)单调递减,故g(x0)

综上所述,k=e-e2.

评注:从分类讨论的角度,先由题目中所给的切线,结合函数的图像分析得到k=e-e2,对于k≠e-e2时,结合x的范围,对函数进行放缩,找到不满足不等式的条件.其中,观察到x=1时取等是解题的关键.该法对学生的数学结合与分类讨论思想要求较高.

(法三)(分离参数)ex-e2lnx≥kx-k+e.

当x<1时,同理可证k≥e-e2.故k=e-e2.

评注:用分离参数,将问题转化为函数最值问题,避免分类讨论,学生更容易入手与解决.易错点在于需对x>1与x<1进行分情况讨论.计算量较大,且应用洛必达法则求x=1处的极限值,超出了高中阶段的学习范畴.