基于改进Radon-wigner 变换的微弱目标加速度估计算法*

祁萍萍，李 琦，韩壮志

（1.河北工业大学电子信息工程学院，天津 300401；2.陆军工程大学石家庄校区电子与光学工程系，石家庄 050003）

0 引言

由于LFMCW 雷达具有截获概率低、近距离分辨率高、体积小和无距离盲区等优点，因此，在汽车防撞、轨道交通、近程防御、测速和测距等领域被广泛应用，其理论与实际应用技术的研究也成为热点问题［1-4］。

LFMCW 雷达通过动目标检测（moving target detection，MTD）处理，可以得到目标的多普勒频谱，进而实现对目标速度的估计。但是，当目标存在加速运动时，加速度会导致多普勒信号频谱展宽，从而影响雷达的目标检测性能［5］。文献［6］提出了一种基于离散Chirp-Fourier 变换的多项式相位参数估计算法，该算法可以对具有加速度的目标进行参数估计，但该方法具有较大运算量，不利于工程实现。

在对微弱目标长时间积累过程中，若目标做匀加速度运动，其差拍信号频谱峰值受到速度和加速度的同时调制形成线性调频（linear frequency modulated，LFM）信号，而LFM 信号的调频率反映了目标的加速度值［7］。虽然传统的RWT 可以在低信噪比下对目标进行有效检测，但要获得高精度估计值需要很大的计算量，因此，改进算法从计算量和估计精度两方面对传统算法进行改进，并且通过仿真实验证明该算法的优越性。

1 差拍信号分析

本文LFMCW 雷达的发射信号采用锯齿波，其产生差拍信号的原理图如图1 所示，其中，f0为载频；B 为信号带宽；T 为调频周期；k=B/T 为调频率。

图1 LFMCW 雷达锯齿波差拍信号产生原理图Fig.1 Schematic diagram of LFMCW radar sawtooth beat signal generation

第m+1 个调频周期的发射信号形式为：

其中，A0为信号幅度。

用t+mT 代替t 来消除调频周期数m 对t 的影响。在实际情况下，加速度对差拍信号载频的影响小，可以忽略不计，并忽略c2、t3项，可得：

一般情况下，式（3）的调频率很小，所以式（3）可以简化为单频信号：

对式（4）进行快时间反转，然后和式（4）相乘，并且为了利用能量对N 组慢时间维信号进行叠加，可得差拍信号频谱峰值为：

由式（5）可知，差拍信号频谱峰值同时受到速度与加速度的调制变成LFM 信号，对加速度的估计转变为对差拍信号频谱峰值的调频率估计。

2 RWT 改进算法的实现

2.1 RWT 的原理

Radon 变换通过旋转坐标投影积分来进行直线搜索，把平面中的直线变换为一个点。如图2 所示，时频坐标系（tm，ω）旋转角度a 得到新坐标系为（u，v），以平行于v 轴的不同u 值进行积分，其结果即为Radon 变换的结果。

图2 RWT 的几何关系Fig.2 Geometric relationship of RWT

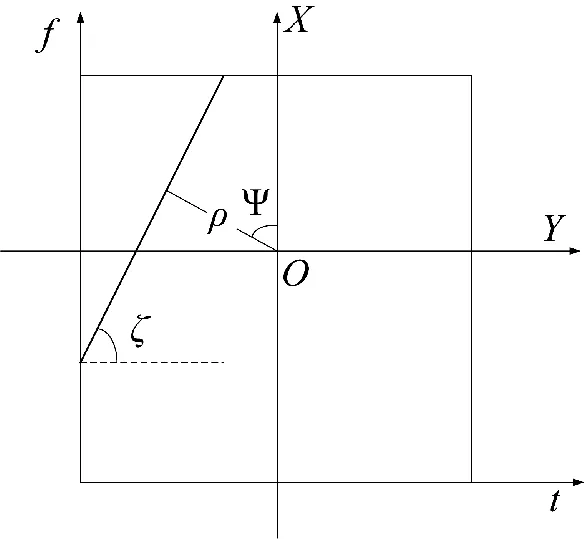
图3 Hough 变换示意图Fig.3 Schematic diagram of Hough transformation

Wigner-Ville 分布（WVD）具有很好的时频聚集性［8］，因此，在时频分析中得到广泛应用。式（5）的Wigner-Ville 分布为：

对式（5）进行RWT 变换，可得：

2.2 熵值法对角度进行粗估计

通过上面分析，可以采用积分求最小熵的方法来估计角度值，搜索公式为：

对式（9）求熵值，可得表达式为：

由熵的物理意义可知，熵最小代表信息量最大，即变化量最大，在二维图像中，图像的峰值越尖锐，熵值越小，在搜索间隔比较大的情况下，每个加速度补偿后的差拍信号频谱峰值幅值相差较大，熵值变化明显，因此，利用这一点可知，最大值对应的角度为最佳角度。

2.3 RWT 的快速算法

由上述可知，RWT 要对调频率和初始频率进行二维搜索，搜索运算量比较大，为了解决这个问题，本节提出一种RWT 的快速算法，通过对RWT 结果进行二阶原点距计算，将二维搜索过程转变为调频率的一维搜索过程。

当旋转角a 为最佳旋转角a0时，信号的分数阶频谱四阶原点矩［10］为：

通过以上分析，可得RWT 的二阶原点矩为：

此时，信号RWT 的二阶原点矩取得最大值。

2.4 精度分析

2.4.1 迭代RWT

由式（15）和式（16）可以发现，在一个周期内，tan、kd、kd的分辨单元Δkd三者呈正相关。因此，在搜索间隔Δ不变的情况下，通过补偿在调频率较大情况下的粗估计，可以使差拍信号的频谱峰值的残留调频率不断减小，调频率的分辨单元也会不断减小，加速度的估计精度更高，此方法多次使用RWT 对调频斜率进行估计称为迭代RWT［12］，可以在计算量较小情况下，获得对差拍信号频谱幅值调频率的精确估计。

2.4.2 RWT 插值方法

插值算法可以在搜索步长设置比较大的情况下，得到精度较高的角度估计值，根据文献［13］的插值算法可知，可以采用如下方法对旋转角度进行插值运算得到真实角度a0的估计值。

情况1 假设RWT 二阶原点距的峰值点对应的角度为ak，若信号的RWT 二阶原点距幅值满足：

则，a0位于ak与ak+1之间，即ak＜a0＜ak+1，可以得到下式：

将式（18）和式（19）取比值后整理可得a0的估计值为：

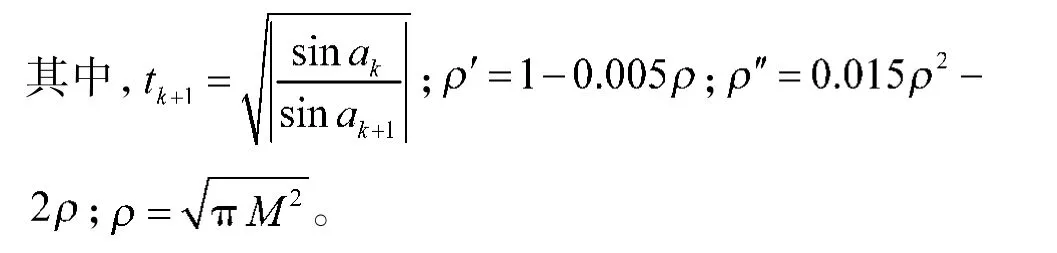
情况2 若LFM 信号的RWT 二阶原点距幅值满足：

则a0位于ak与ak-1之间，即ak-1＜a0＜ak，可得：

将式（22）和式（23）取比值后整理可得a0的估计值为：

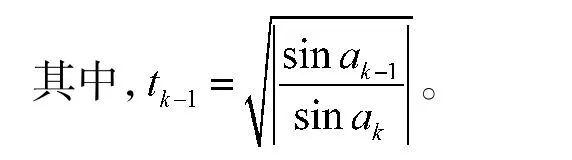
2.5 改进算法流程及计算量分析

通过上述分析，可得改进算法的具体步骤如下：

Step 1 在［0°，180°］内以1°为间隔求在各个角度下差拍信号频谱峰值补偿后的熵值，对熵值取倒数，取最大值对应的角度为最佳角度，通过所得角度求得第1 次加速度估计值，对信号进行补偿得到。

Step 2 对RWT 求二阶原点矩，在［89.5°，90.5°］区间内以0.1°为搜索间隔，对信号内进行角度一维搜索，对搜索得到的角度以0.1*（0.1）R-2（R 表示加速度估计次数）的插值间隔进行插值，得到真实角度估计值，通过所得真实角度估计值求得加速度估计值，与上次加速计估计值相加，得到第2 次加速度估计值，对信号进行补偿得到。

Step 3 重复Step 2，直到第R 次加速度的估计误差小于预定门限。

此方法完成1 次搜索包括1 次RWT 运算和1次RWT 二阶原点矩运算。每提高一次精度，最多需要增加12 次RWT 运算和10 次RWT 二阶原点矩运算，相比于传统RWT 以0.1°在0°～180°范围内进行1 800 次二维搜索，大大减少了计算量。

3 实验与分析

为了验证理论分析的正确性，对上述分析进行了仿真实验。假设目标匀速运动，载频f0=24 GHz，信号带宽B=150 MHz，调频周期数M=500，调频周期T=100 us，距离维采样点数为N=512，目标初始速度V0=20 m/s，初始距离R0=100 m，加速度a=15 m/s2，输入信噪比SNR=-14 dB。

3.1 角度粗估计

利用熵值法对角度的估计如图4 所示。由图可知，当位于最佳角度时差拍信号的频谱峰值的熵值倒数最大，因此，可以通过对熵值倒数的峰值点检测来获得角度的粗估计值。

图4 差拍信号频谱峰值熵值倒数Fig.4 Reciprocal entropy value of beat signal spectrum peak value

当搜索间隔为1°时，在不同的加速度条件下对熵值法、RWT 搜索到的角度进行比较，如表1 所示，可以看出熵值法和RWT 在大搜索间隔下得到角度相同，但熵值法用时更短，估计速度更快。

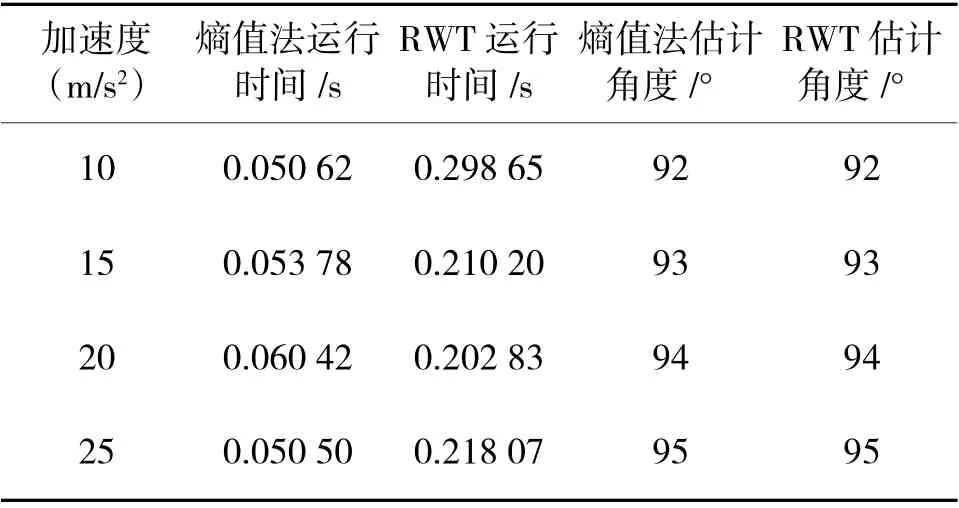
表1 不同加速度时角度估计及估计速度Table 1 Angle estimation and estimated velocity under different accelerations

3.2 RWT 积累结果

由图5（a）可知，信号的RWT 变换呈现峰值，即此方法有效地实现了频谱峰值信号能量积累，通过峰值检测可实现微弱目标的加速度估计。但是，图5（a）在不同角度下噪声的大小相差较大且噪声幅值与信号的幅值相差较小，这对二阶原点矩的求取带来困难。为了解决上述问题，本文首先对WVD 的结果进行四次方处理，再对其进行Radon 变换，结果如图5（b）所示。由图5（b）可知，此时噪声幅值与信号幅值相差较大，降低了噪声对RWT 二阶原点矩的干扰。

图5 RWT 积累结果Fig.5 RWT accumulation results

3.3 RWT 的二阶原点矩

对RWT 结果进行二阶原点矩计算，仿真结果如下：

1）对WVD 分布直接进行Radon 变换、二阶原点矩计算，如图6（a）所示，由上述分析可知，此时RWT 二阶原点矩受噪声影响比较大。

图6 RWT 的二阶原点矩Fig.6 Second order origin moment of RWT

2）对WVD 分布进行四次方处理后，再进行Radon 变换、二阶原点矩计算，如图6（b）所示，此时可以通过尖峰位置获得最佳旋转角，从而进行加速度的准确估计。

与上面二维搜索相比，RWT 二阶原点矩只需一维峰值搜索即可实现信号检测以及最佳旋转角度的估计，计算量小于二维搜索法。

3.4 计算量比较及精度分析

为了验证改进算法的计算量，对传统方法RWT、迭代RWT、一次插值、二次插值进行对比研究，仿真结果如表2 所示。可以看出传统RWT 要进行1 800 次RWT 运算，计算量较大，加速度均方误差也大，二次插值比迭代RWT 多4 次RWT 运算，加速度的均方误差却减小了很多，加速度估计更加精确。

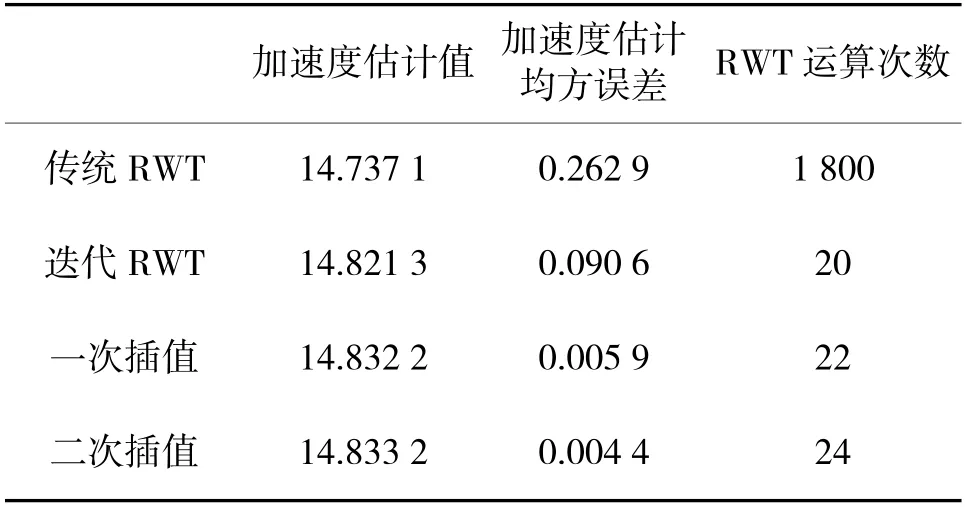
表2 4 种算法仿真结果Table 2 Simulation results of four kinds of algorithms

在输入信噪比为-10 dB 情况下，对目标进行3次加速度估计，为了方便描述，把在第2 次加速度估计时应用RWT 插值方法简称为一次插值，在第2次和第3 次加速度估计时应用RWT 插值方法简称为二次插值，比较迭代RWT，一次插值，二次插值的加速度估计均方误差，如表3 所示，可以看出在搜索间隔不变的情况下，迭代RWT 可以提高加速度估计精度，通过一次插值后，加速度的均方误差显著降低，经过二次插值后，加速度的均方误差较一次插值更低，说明在迭代RWT 中应用RWT 插值方法可以提高加速度的估计精度。

表3 加速度估计值的均方根误差Table 3 Root mean square error of acceleration estimated values

在上述条件不变的情况下，比较迭代RWT、一次插值、二次插值在不同加速度情况下经过3 次加速度估计后的加速度均方误差，如表4 所示，由表4可以看出不同加速度情况下，上述结论仍成立。

表4 不同加速度情况下加速度估计值的均方根误差Table 4 Root mean square errors of acceleration estimated valuesunder different acceleration conditions

为了进一步对精度进行分析，本文在［-16，0］dB的信噪比范围内，进行了100 次蒙特卡罗仿真实验，对迭代RWT、一次插值、二次插值，与传统RWT的1 800 次二维搜索的加速度估计的均方根误差进行比较分析，得到加速度均方根误差随输入信噪比（SNR）的变化关系。实验结果如下页图7 所示，可以看出在信噪比大于-15 dB 情况下，本文方法经过两次插值相比于传统RWT 和迭代RWT，在低信噪比情况下具有更好的估计精度。

图7 加速度均方根误差曲线Fig.7 Acceleration root mean square error curve

4 结论

在低信噪比环境下，对匀加速微弱目标的检测是LFMCW 雷达的一个技术难点，本文提出的改进RWT 大大降低了计算量，显著提高了目标加速度的估计速度和精度。通过理论分析和仿真结果表明，改进算法可以在低信噪比下以较小的计算量得到高精度的加速度估计值，本文为微弱目标的检测提供了一条可选择途径。虽然该方法相对于传统RWT的运算速度和精度有所提升，但是由于对时频分析过程中运算较大，实时性能较差，因此，找到计算量更小，实时性更好的方法是今后的研究重点。