2023全国高中数学联合竞赛（预赛B卷）第7题的求解、变式与拓展探究

周秀玲 李加翔

【摘要】高中数学竞赛不仅可以培养学生的逻辑思维能力和解决数学问题的能力，还可以激发学生对数学的兴趣，以及拓宽数学视野.在高中数学竞赛试题的解答过程中，解题思路和方法非常重要，学生需要培养灵活的思维方式，学会一题多角度思考，本文以2023全国高中数学联合竞赛（预赛B卷）第7题为例，对试题进行求解、变式以及推广到一般结论，希望能够拓宽学生的解题思路，提升数学思维能力.

【关键词】高中数学；解题技巧；一题多解

竞赛试题  2023全国中学生数学奥林匹克竞赛·预赛（B卷·第7题）设P－ABCD与Q－ABCD为两个正四棱锥，且∠PAQ=90°，点M在线段AC上，且CM=3AM.将异面直线PM，QB所成的角记为θ，则cosθ可能的最大值为（  ）

1  试题分析与求解，专注于一道题

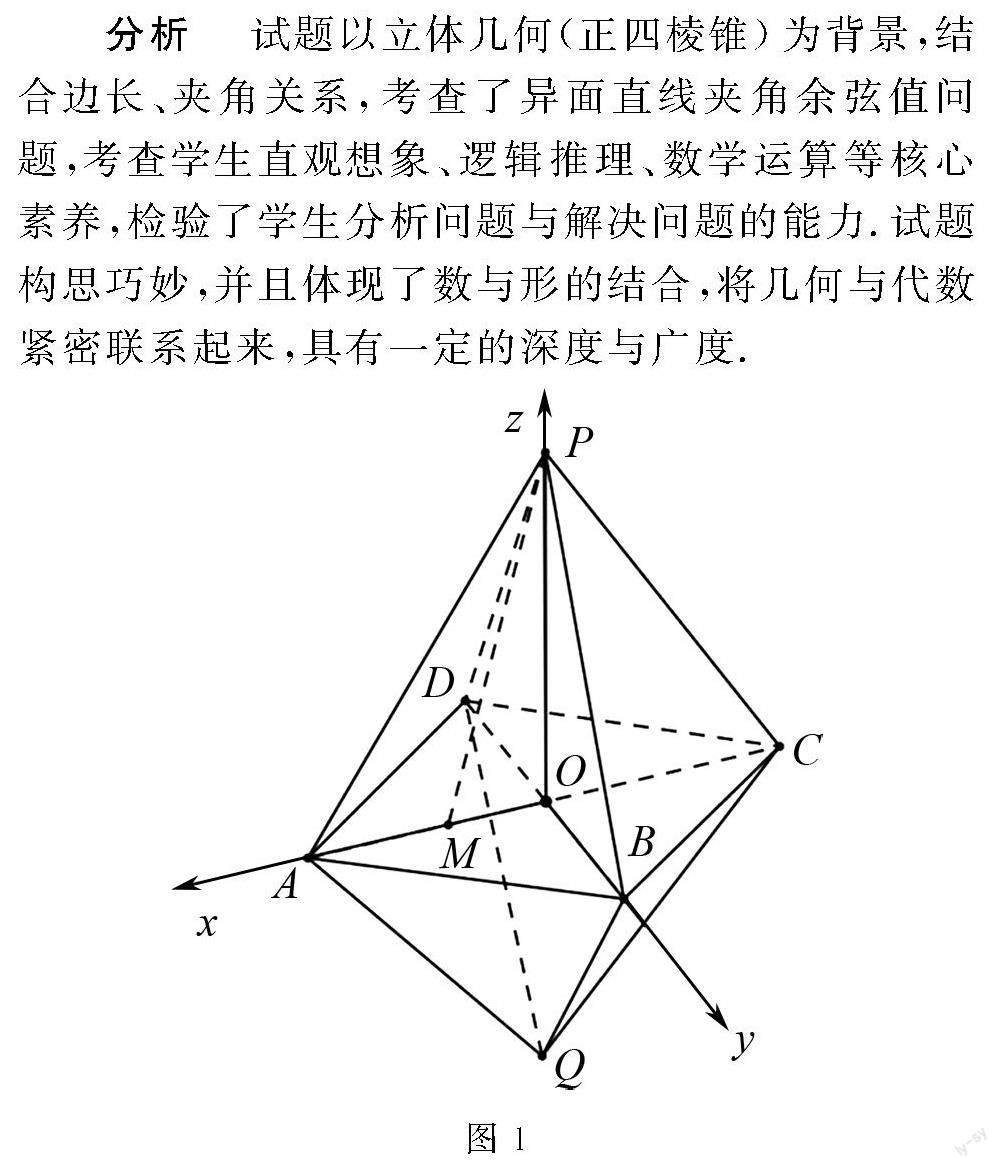
分析  试题以立体几何（正四棱锥）为背景，结合边长、夹角关系，考查了异面直线夹角余弦值问题，考查学生直观想象、逻辑推理、数学运算等核心素养，检验了学生分析问题与解决问题的能力.试题构思巧妙，并且体现了数与形的结合，将几何与代数紧密联系起来，具有一定的深度与广度.

图1

求解  如图1所示，因为P－ABCD与Q－ABCD为两个正四棱锥，所以四边形ABCD为正方形，假设O为正方形ABCD的中心，依题意可知PQ垂直与平面ABCD，且经过点O，OA⊥OB，

以O为坐标原点，OA，OB，OP分别为x，y，z轴正方向建立空间直角坐标系，

假设正方形ABCD边长为2，

则OA=OB=1，

设∠PAC=α，（0<α<90°），

因为∠PAQ=90°，

所以∠APO=90°－α，∠OAQ=90°－α，

在直角PAO中：

tan∠APO=tan（90°－α）=AOPOPO

=1tan（90°－α），

同理，在直角PAQ中，

tan∠OAQ=tan（90°－α）=OQOAOQ=OA·tan（90°－α）=tan（90°－α），

又因为A（1，0，0），B（0，1，0），P（0，0，1tan（90°－α）），Q（0，0，－tan（90°－α）），M（12，0，0），

所以PM=12，0，-1tan（90°-α），

QB=（0，1，tan（90°-α）），

所以cosθ=PM·QBPMQB

=-1tan（90°-α）·tan（90°-α）  14+1tan2（90°-α）·  1+tan2（90°-α）

=1  14+tan2（90°-α）4+1tan2（90°-α）+1

对tan2（90°－α）4+1tan2（90°－α）进行分析，

因为∠PAC=α，（0<α<90°），

所以tan（90°－α）恒大于0，

所以tan2（90°－α）4>0，1tan2（90°－α）>0，

運用基本不等式：

tan2（90°－α）4+1tan2（90°－α）≥

2tan2（90°－α）4·1tan2（90°－α）=2·12=1.

当且仅当tan2（90°－α）4=1tan2（90°－α）时，取等号，

即tan4（90°－α）=4tan（90°－α）=2.

cosθ=114+tan2（90°－α）4+1tan2（90°－α）+1

≤114+1+1=23.

解法点评  以上介绍的解法体现了数形结合的思想，结合正四棱锥的图形特征，PQ⊥平面ABCD，以O为坐标原点，OA，OB，OP分别为x，y，z轴正方向建立空间直角坐标系，充分利用“坐标法”原理，将几何问题代数化，解答过程中考查了平面向量、正切值定义、异面直线夹角公式以及基本不等式等知识点，这也体现了竞赛试题知识点考查交汇融合的特点，这就要求学生在平时的学习过程中，注重知识的融合，学会灵活运用知识.

针对于此试题，可以改变题目部分条件，进行进一步的研究和拓展，以下从3个视角进行探究分析.

2  试题变式推广，由会解一道题到会解一类题

视角1  推广［变参数比值：CM=λAM.（λ>1）］

设P－ABCD与Q－ABCD为两个正四棱锥，且∠PAQ=90°，点M在线段AC上，且CM=λAM（λ>1），将异面直线PM，QB所成的角记为θ，则cosθ可能的最大值为（  ）

求解  因为P－ABCD与Q－ABCD为两个正四棱锥，所以四边形ABCD为正方形，假设O为正方形ABCD的中心，依题意可知PQ垂直于平面ABCD，且经过点O，

以O为坐标原点，OA，OB，OP分别为x，y，z轴正方向建立空间直角坐标系，假设正方形ABCD边长为2，

设∠PAC=α，（0<α<90°），因为∠PAQ=90°，

所以∠APO=90°－α，∠OAQ=90°－α，在直角PAO中，

tan∠APO=tan（90°－α）=AOPOPO=1tan（90°－α），同理，在直角PAQ中，

tan∠OAQ=tan（90°－α）=OQOAOQ=OA·tan（90°－α）=tan（90°－α），

因为CM=λAM.所以λAM+AM=2（对角线长为2），AM=21+λ，

又因为A（1，0，0），B（0，1，0），P（0，0，1tan（90°－α）），Q（0，0，－tan（90°－α）），M（1－21+λ，0，0），

所以PM=1-21+λ，0，-1tan（90°-α），

QB=（0，1，tan（90°-α）），

所以cosθ=｜PM·QB｜PMQB

=-1tan（90°-α）·tan（90°-α）  λ-11+λ2+1tan2（90°-α）·  1+tan2（90°-α）

=1λ－11+λ2+1tan2（90°－α）+（λ－1）2tan2（90°－α）（λ+1）2+1

對（λ－1）2tan2（90°－α）（λ+1）2+1tan2（90°－α）进行分析，

因为∠PAC=α，（0<α<90°），（λ>1），

所以tan（90°－α）恒大于0，

所以（λ－1）2tan2（90°－α）（λ+1）2>0，

1tan2（90°－α）>0，

运用均值不等式：

（λ－1）2tan2（90°－α）（λ+1）2+1tan2（90°－α）≥2（λ－1）2tan2（90°－α）（λ+1）2·1tan2（90°－α）=2（λ－1）2（λ+1）2.当且仅当（λ－1）2tan2（90°－α）（λ+1）2=1tan2（90°－α）tan2（90°－α）=λ+1λ－1.时，取等号，

cosθ=1λ－11+λ2+tan2（90°－α）4+（λ－1）2tan2（90°－α）（λ+1）2+1

≤11+2（λ－1）2（λ+1）2+（λ－1）2（λ+1）2

≤1（1+λ－1λ+1）2=11+λ－1λ+1=λ+12λ.

点评  通过推广探究，我们初步得知：异面直线PM，QB所成的角cosθ可能的最大值与CM、AM的参数比值有关，当CM=λAM.（λ>1）时，cosθmax=λ+12λ.这是从边长关系角度思考，那学生也可以从角度方向进行探究，异面直线PM，QB所成的角cosθ可能的最大值是否与∠PAQ的角度大小有关？

视角2  推广［变角度：∠PAQ=β，（0<β<90°），变参数比值CM=λAM（λ>1）］

.设P－ABCD与Q－ABCD为两个正四棱锥，且∠PAQ=β，点M在线段AC上，且CM=λAM.将异面直线PM，QB所成的角记为θ，则cosθ可能的最大值为（  ）

求解  因为P－ABCD与Q－ABCD为两个正四棱锥，所以四边形ABCD为正方形，假设O为正方形ABCD的中心，依题意可知PQ垂直于平面ABCD，且经过点O，

以O为坐标原点，OA，OB，OP分别为x，y，z轴正方向建立空间直角坐标系，假设正方形ABCD边长为2，

设∠PAC=α，（0<α<β）因为∠PAQ=β，

所以∠APO=90°－α，∠OAQ=β－α，

在直角PAO中：

tan∠APO=tan（90°－α）=AOPOPO

=1tan（90°－α），

同理，在直角PAQ中，

tan∠OAQ=tan（β－α）=OQOAOQ=OA·tan（β－α）=tan（β－α），

因为CM=λAM.所以λAM+AM=2，

AM=21+λ，

又因为A（1，0，0），B（0，1，0），P（0，0，1tan（90°－α）），Q（0，0，－tan（β－α）），M（1－21+λ，0，0），

所以PM=1-21+λ，0，-1tan（90°-α），

QB=（0，1，tan（β-α）），

所以cosθ=｜PM·QB｜PMQB

=-1tan（90°-α）·tan（β-α）  λ-11+λ2+1tan2（90°-α）·  1+tan2（β-α）

=tan（β－α）tan（90°－α）λ－11+λ2+1tan2（90°－α）+

tan（β－α）

（λ－1）2tan2（90°－α）（λ+1）2+tan2（β－α）tan2（90°－α）

=tan（β－α）（λ－1）2tan2（90°－α）1+λ2+1+

tan（β－α）

（λ－1）2tan2（90°－α）（λ+1）2+tan2（β－α）

因为tan（β－α）

所以cosθ≤tan（β－α）（λ－1）2tan2（β－α）1+λ2+1+

tan（β－α）

（λ－1）2tan4（β－α）（λ+1）2+tan2（β－α）

=1（λ－1）21+λ2+1tan2（β－α）+

1

（λ－1）2tan2（β－α）（λ+1）2+1

对1tan2（β－α）+（λ－1）2tan2（β－α）（λ+1）2进行分析，

因为∠PAC=α，（0<α<β），（λ>1），

所以tan（β－α）恒大于0，

所以（λ－1）2tan2（β－α）（λ+1）2>0，

1tan2（β－α）>0，

运用均值不等式：

（λ－1）2tan2（β－α）（λ+1）2+1tan2（β－α）≥2（λ－1）2tan2（β－α）（λ+1）2·1tan2（β－α）

=2（λ－1）2（λ+1）2.当且仅当（λ－1）2tan2（β－α）（λ+1）2=1tan2（β－α）tan2（β－α）=λ+1λ－1时，取等号，

cosθ≤1λ－11+λ2+1tan2（β－α）+（λ－1）2tan2（β－α）（λ+1）2+1

≤11+2（λ－1）2（λ+1）2+（λ－1）2（λ+1）2

≤1（1+λ－1λ+1）2=11+λ－1λ+1=λ+12λ.

结论  改变原试题条件变角度：∠PAQ=β，（0<β<90°），变参数比值CM=λAM（λ>1），cosθ的最大值只与参数比值λ有关，与β的具体数值没有关系，

并且cosθmax=λ+12λ.

延申拓展  （1）∠PAQ=β，（β>90°），CM=λAM（λ>1），cosθ的最大值是否存在？若存在，求出最大值，若不存在，说明理由.

（2）∠PAQ=β，（β>90°），CM=λAM.（0<λ<1），cosθ的最大值是否存在？若存在，求出最大值，若不存在，说明理由.

3  结语

一题一世界，一思一成功，以上从5个视角，从不同的角度思考与分析问题，循序渐进，最终推广到一般结论，这充分体现了竞赛试题不拘一格，一道试题往往可以从不同角度进行改编，探索研究.思维方式不是唯一的，数学结论也不是唯一的，但数学的“本质”，数学的“味道”是相似的，万变不离其宗，这给学生的思维训练提供了很大的发展空间.学数学离不开解题，而解题离不开思考，学而不思则罔，当遇到一道经典试题，首先要对试题进行求解，其次需要从多角度，深层次探索问题的“本质”，这样才能解一题会一类，做到触类旁通，成为真正的数学学习者.

參考文献：

［1］李勇.对2020年全国高中数学联合竞赛第4题的多视角探究［J］.高中数理化，2022（03）：3-5.

［2］鞠妍，刘施樑.对一道全国高中数学联合竞赛题的探究［J］.数学教学，2020（11）：42-43.

［3］张君.2023年全国高中数学联赛（四川预赛）试题及解析［J］.数理化解题研究，2023（28）：88-92.