一类具有垂直传染的传染病模型的稳定性

郝艳荣,赵春

(天津师范大学数学科学学院,天津 300387)

1.引言

传染病一旦出现以及蔓延会严重危及人类生命健康,尤其面对新型复杂的传染病类型,初期只能从宏观上对其进行预防和控制,很难科学地从根本上进行防控,因此及时发现并探究各类传染病的内在传播机制是极为重要的.通过建立传染病动力学模型可有效的描述疾病发展变化的过程和传播规律,预测疾病发展趋势,并能为预防控制疾病提供决策依据.为了使模型更加符合实际,许多关于传染病模型的文献考虑了不同的仓室并讨论了相应模型的稳定性[1].文[2]以COVID-19为背景,研究了基于存在基础病史易感者的SEIR模型的稳定性.文[3]在假设总人口为常数的情况下研究了一类具有水平和垂直传播的传染病模型.文[4]基于LI等人的研究进一步讨论了一类含潜伏期,染病者有病死且具标准传染率的SEIR传染病模型.文[5]针对COVID-19的传播特性和新生儿患病案例的出现,提出了一类具有垂直传染风险及潜伏者感染性的SEIR传染病动力学模型.文[6]研究了一类具有垂直传播和饱和发病率的传染病模型.但是在具有基础病史易感者的基础上考虑垂直传染的研究还较少,本文在二者结合的基础上,增加了隔离治疗者仓室,建立了一类具有垂直传染的传染病模型.

2.模型的建立

本文模型共建立六个仓室,分别为无基础病史的易感者(S1),有基础病史的易感者(S2),具感染的潜伏者(L),染病者(I),隔离治疗者(Q)和移出者(R).假设母体为有基础病史的新生儿为无基础病史易感者;母体为具感染的潜伏者,染病者和隔离治疗者的新生儿具被垂直传染的可能;隔离治疗者不具备传染他人的可能以及该疾病无因病致死的可能.所以,根据传染病的动力学方法建立如下传染病模型:

其中N(t)=S1(t)+S2(t)+L(t)+I(t)+Q(t)+R(t),模型中的参数均为正常数.β1是因具感染的潜伏者由S1转为L的传染率.β2是因染病者由S1转为L的传染率.β3是因潜伏感染由S2转为L的传染率.β4是因染病者由S2转为L的传染率.b是自然出生率.p是垂直传染率.µ是自然死亡率.ξ是由S1转为S2的转移率.δ是由L转为I的转移率.η是由I转为Q的转移率.θ是由L转为Q的转移率.γ是由Q转为R的恢复率.初始条件N(0)=S1(0)+S2(0)+L(0)+I(0)+Q(0)+R(0),S1(0)>0,S2(0)>0,L(0)>0,I(0)>0,Q(0)>0,R(0)>0.

下面说明系统(2.2)所有满足初始条件的解的正定性和有界性.

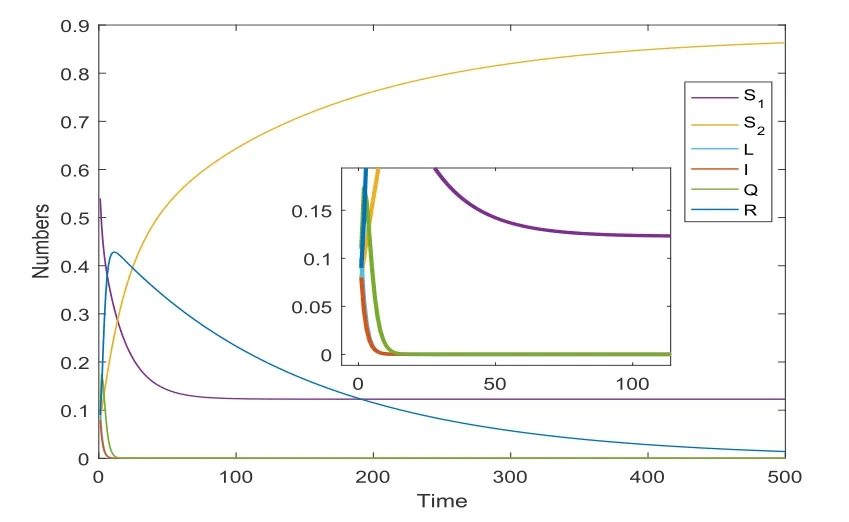
定理2.1对任意t>0,系统(2.2)所有满足初始条件的解(S1(t),S2(t),L(t),I(t),Q(t),R(t))均满足0

证首先,对系统(2.2)的第一式有

即

令t1=sup{t>0 :S1(t)>0,S2(t)>0,L(t)>0,I(t)>0,Q(t)>0,R(t)>0}>0,则当t ∈(0,t1]时,式(2.3)可写为

再令t2=sup{t>t1:S1(t)>0,S2(t)>0,L(t)>0,I(t)>0,Q(t)>0,R(t)>0}>0,则当t ∈(t1,t2]时,有

依次向后延拓,可得对任意t>0,S1(t)>0成立.同理对系统(2.2)还可证得对任意t>0,S2(t)>0,L(t)>0,I(t)>0,Q(t)>0,R(t)>0均成立[7].又N∗=S1(t)+S2(t)+L(t)+I(t)+Q(t)+R(t),所以对任意t>0,系统(2.2)所有满足初始条件的解(S1(t),S2(t),L(t),I(t),Q(t),R(t))均满足0

因系统(2.2)中只有第6个方程含有R,故可以只考虑以下系统:

通过以上分析,可得系统(2.4)有正不变集D={(S1(t),S2(t),L(t),I(t),Q(t))∈R5|S1(t)+S2(t)+L(t)+I(t)+Q(t)0,S2(t)>0,L(t)>0,I(t)>0,Q(t)>0}.

3.平衡点和基本再生数

令x=(L,I,Q,S1,S2)T,则系统(2.4)可改写为矩阵形式

计算F(x)和V(x)的Jacobian矩阵,得：

从而,F(x)和V(x)在无病平衡点处的Jacobian矩阵分别为：

进而,借助下一代矩阵法[8],得到系统(2.4)的基本再生数R0的表达式,即

且显然m1,m2,m3均大于0.

下面求系统(2.4)的地方病平衡点E∗=(,,L∗,I∗,Q∗).

首先,由f1(t)=0,f2(t)=0,f4(t)=0和f5(t)=0得

且f′(I)<0,即f(I)是区间[0,N∗]上关于I的单调递减函数.由根的唯一性定理,当且仅当满足条件f(0)>0,即R0>1时,方程f(I)=0在区间(0,N∗)上有唯一根.所以,当R0>1,b>m3时,可知系统(2.2)存在唯一的地方病平衡点E∗.

此外,将f(I)=0整理为一元二次方程形式,有

其中

易知a1<0,方程(3.2)有唯一正根

通过以上的分析,得出以下地方病平衡点的存在唯一性定理.

定理3.1若R0>1,b>m3,则系统(2.4)的地方病平衡点E∗存在且唯一.

4.平衡点的稳定性

定理4.1若R0<1,η>γ,则系统(2.4)在无病平衡点E0处局部渐近稳定;若R0>1,则系统(2.4)在无病平衡点E0处不稳定.

证系统(2.4)的Jacobian矩阵为

在无病平衡点E0处有

由此得到两个具有负实部的特征根λ1=-ξ-µ,λ2=-µ,且其余特征根λ3,λ4,λ5满足

进而，可知当R0<1时,

同时,当η>γ时,

根据Routh-Hurwitz判别法[9],当R0<1,η>γ时,方程(4.1)的一切根具有负实部,进而证得系统(2.4)在无病平衡点E0处局部渐近稳定.

当R0>1时,显然a6<0,由根与系数的关系知

故λ3,λ4,λ5中至少有一个正根,所以在无病平衡点E0处不稳定.

定理4.2若R0<1,则系统(2.4)在无病平衡点E0处全局渐近稳定.

证构造Lyapunov函数

其中ui(i=1,2,3)为待定的正数.易知只有在无病平衡点E0处,V1=0.否则,V1>0.现对V1关于系统(2.4)求导,可得

下面讨论地方病平衡点的局部渐近稳定的充分条件.

易知系统(2.4)在地方病平衡点E∗处的Jacobian矩阵为

则A|E∗对应的特征方程如下

可列出相应的劳斯表,如表4.1 所示,其中

表4.1 劳斯表

由Routh判据[11]知,当R0>1,b>m3,ai>0(i=7,···,11),b1>0,c1>0,d1>0时,系统(2.4)在地方病平衡点E∗处局部渐近稳定.综上可得如下结论:

定理4.3若R0>1,b>m3,ai>0(i=7,···,11),b1>0,c1>0,d1>0,则系统(2.4)的地方病平衡点E∗是局部渐近稳定的.

定理4.4若R0>1,b>m3,则系统(2.2)存在唯一的地方病平衡点且在其地方病平衡点处全局渐近稳定.

5.数值模拟和讨论

下面进行数值模拟,验证稳定性的主要结论.

对系统(2.4),取初始值S1(0)=0.54,S2(0)=0.08,L(0)=0.1,I(0)=0.08,Q(0)=0.11,R(0)=0.09及参数β1=0.3,β2=0.35,β3=0.4,β4=0.55,δ=0.3,η=0.8,ξ=0.05,γ=0.45,θ=0.5,b=0.007,p=0.003,µ=0.007.经计算知,此时基本再生数R0=0.7226<1.同时,观察图5.1,得系统(2.4)在无病平衡点处全局渐近稳定.

图5.1 无病平衡点的稳定性

同样的,取系统(2.2)中的初始值S1(0)=0.54,S2(0)=0.08,L(0)=0.1,I(0)=0.08,Q(0)=0.11,R(0)=0.09及参数β1=0.45,β2=0.6,β3=0.5,β4=0.664,δ=0.15,η=0.85,ξ=0.05,γ=0.25,θ=0.4,b=0.007,p=0.003,µ=0.007,得基本再生数R0=1.0929>1.此时,图5.2显示呈渐近稳定性态,说明系统(2.2)的地方病平衡点是全局渐近稳定的.

图5.2 地方病平衡点的稳定性