一种近似BFGS的自适应双参数共轭梯度法

李向利 ,莫元健 ,梅建平

(1.桂林电子科技大学数学与计算科学学院,广西 桂林 541004;2.广西高校数据分析与计算重点实验室,广西 桂林 541004;3.广西应用数学中心,广西 桂林 541004)

1.引言

常见无约束优化问题：

其中x ∈Rn表示可行域,f(x)为可行域内的连续可微函数,g(x)为f(x)的梯度其计算表达式为g(x)=∇f(x).

最早求解问题(1.1)的方法有牛顿法,拟牛顿法等.但是这些方法并不适用在大规模问题上,因为它们需要计算和存储Hessian矩阵或其近似值,这使得计算成本非常昂贵.共轭梯度法因其低存储、易计算和具有良好收敛性等特点进而被广泛应用在求解大规模无约束优化问题当中.

针对问题(1.1),共轭梯度法的近似解序列{xk}迭代格式如下:

其中αk、dk分别表示步长和搜索方向.步长αk通常由Wolfe[1]线搜索可得

其中ρ和σ满足关系0<ρ≤σ<1.搜索方向dk可根据以下公式计算:

目前研究者们提出了一系列新的共轭梯度法,这些共轭梯度法的推广研究主要集中在共轭参数和搜索方向的选取上.其中一些经典的共轭参数βk如下: Fetcher-Reeves(FR)[2],Polak-Ribière-Polyak(PRP)[3-4],Hestenes-Stiefel(HS)[5],共轭下降(CD)[6],Liu-Storey(LS)[7],和Dai-Yuan(DY)[8].对应的βk公式分别为

其中∥.∥表示欧几里得范数,yk=gk+1-gk.

拟牛顿法[9]也常用于求解大规模无约束优化问题.由Broyden[10]、Fletcher[11]、Goldfard[12]、Shanno[13]四位学者提出的BFGS方法是最有效的拟牛顿方法之一.为了更有效的求解大规模无约束优化问题,进一步减少计算和储存空间成本,将共轭梯度法和拟牛顿法相结合的研究已成热门趋势,众多学者对这两种方法的优化和改进仍在继续.

在共轭梯度法中,标准的共轭条件可以让其获得良好的数值结果和收敛性,但标准的共轭条件在非精确线搜索中不能保证充分下降性,为了解决这一缺陷,DAI和LIAO[14]把拟牛顿法的思想用到共轭梯度法中,则有DAI-LIAO共轭条件:

其中τ是DAI-LIAO参数,此时共轭梯度参数迭代更新公式为

其中τ≥0,当τ=0时,上式退化为许多学者对(1.7)中的参数τ进行研究,学者Hager和ZHANG[15]基于HS法提出著名的CGDESCENT共轭梯度法,其搜索方向满足充分下降性和共轭条件,CGDESCENT法可看作DL共轭梯度法的一种特殊形式,搜索方向为

DAI和KOU[16]结合最佳逼近思想,使得共轭梯度法的搜索方向逼近Perry和Shanno[17]的自适应无记忆BFGS方法的搜索方向,提出一类新的共轭梯度法.LI[18]受文[16]的启发提出一个三项PRP 共轭梯度方法,其搜索方向接近无记忆BFGS拟牛顿方法的方向,在强Wolfe条件下,搜索方向满足充分下降性,搜索方向为

Jitsupa[19]受文[18]的启发提出了一种新的混合共轭梯度算法来求解问题(1.1).该混合共轭梯度算法的方向是由共轭参数CD和DY组合而成并且接近无记忆BFGS拟牛顿算法的方向.在Wolfe条件和其他适当的假设下,该算法的充分下降性和全局收敛得到证明,其搜索方向为

受以上文献设计搜索方向参数思路的启发,为了更加有效的求解大规模无约束优化问题,本文考虑让搜索方向接近文[20-21]中无记忆BFGS方法的方向,并构造一个新的自适应双参数共轭梯度法.

本文的其余部分框架如下.第2节,设计一个有效的自适应双参数共轭梯度算法.第3节,在一般假设条件下,给出算法在标准Wolfe线搜索下的全局收敛性证明.第4节,对算法的数值实验结果进行分析.第5节,对全文进行总结.

2.TTNEWCG算法

求解问题(1.1) 的三项共轭梯度方法一般计算搜索方向如下:

其中βk-1和rk为参数,参数的选取不同所对应的共轭梯度算法也不同.当(2.1)中的rk=0 时,此时的三项共轭梯度法变为经典共轭梯度法.文[20-21]提出的无记忆BFGS方法的该搜索方向如下:

其中,I是单位矩阵.公式(2.2)中搜索方向可以写成如下形式:

公式(2.4)中设计的自适应参数tk通过搜索方向接近无记忆BFGS搜索方向获得,再通过单变量最小化问题计算tk表达式如下:

搜索方向下降性对收敛性分析有着重要作用,为保证算法生成的搜索方向满足充分下降性,因此,本文通过定理2.1说明公式(2.7)的搜索方向满足充分下降性.

证结合(2.7)计算易得

下面对自适应双参数tk和mk的取值范围进行讨论.

为提高算法效率来得到更好的数值结果,本文采用加速算法来替代公式(1.2)的最小点,并记为

本文提出一种有效的自适应双参数三项共轭梯度算法,该方法能更有效的求解大规模无约束优化问题,新算法的具体步骤如下:

算法2(TTNEWCG)

3.收敛性分析

在本节,我们证明TTNEWCG算法的全局收敛性.证明过程需做出如下合理假设:

假设3.1

1) 水平集Ω={x ∈Rn|f(x)≤f(x0)}是有界的;

2) 在Ω的某个邻域N内,函数的梯度f(x)在水平集Ω上满足Lipschitz连续,即存在一个常数L>0,使得

上面假设1)2)可等价于存在非负常数γ1和B满足

又由式(3.3)易得

除了上述假设外,为了更好的证明TTNEWCG算法的理论性质,下面给出引理3.1来说明新设计的搜索方向满足充分下降性.

引理3.1若搜索方向dk+1由算法TTNEWCG生成,则搜索方向dk+1具有充分下降性,即存在一个常数c>0使得

根据公式(2.7)-(2.10)可知该搜索方向满足充分下降性.因此,TTNEWCG方法定义良好.

Zoutendijk条件[23]对证明共轭梯度法的全局收敛性起重要作用,在标准的wolfe线搜索条件下,Zoutendijk条件由下面引理3.2给出.

引理3.2[23]若假设3.1成立,近似序列解{xk}由TTNEWCG算法生成,且搜索方向{dk}满足充分下降性,步长αk通过wolfe线搜索得到,那么有

下面利用引理3.1-3.2对新算法TTNEWCG进行全局收敛性证明.

定理3.1若假设3.1成立,搜索方向{dk}是由TTNEWCG 算法生成,步长αk通过wolfe 线搜索得到,那么有

证利用反证法,若公式(3.7)不成立,则存在一个常数µ>0有

根据公式(3.1)和(3.4)易知

根据wolfe准则易得

再根据公式(1.4)可得

对式(3.11)进行移项可得

结合式(3.12)和(3.13)有

再根据引理3.1和引理3.2及公式(3.8)可以得到

又由假设3.1和公式(2.7)易得

式(3.16)通过三角不等式可得

将式公式(3.2),(3.4),(3.14)代入式(3.17)可得

由引理3.2知这与式(3.15)矛盾,所以式(3.8)不成立,故得证.

4.数值实验

在本节,将展示利用TTNEWCG算法计算测试问题的数值结果来验证新算法的有效性,在操作系统Win10,PC(CPU 2.40GHz 16.0GB)环境下,利用MatlabR2020a编译代码进行实验.从文[24]中挑选46个测试函数来解决138个测试问题.

对比的测试算法和新算法的搜索方向具有相似结构,本文用TTNEWCG方法和文[19]中的TTCDDY方法、文[8]中的DY方法、文[15]中的CGDESCENT方法、文[18]中的TPRP方法进行比较,所有算法都在标准Wolfe非精确线搜索下进行,参数设置为:ρ=0.001,σ=0.8,t=1,λ=2.01.算法的终止准则为: Iter>2000或∥gk∥≤10-5(1+|fk|).

表2显示在1000,5000,10000维度条件下五个对比算法的数值结果,N代表函数名称,dim代表维度,Iter,Fno,Gno,Time分别代表算法迭代次数,目标函数迭代次数,目标梯度迭代次数和CPU运行时间.表格中的“NAN”代表该方法存在数值溢出或者未能达到算法的收敛条件.表1为测试函数的序号及名称.

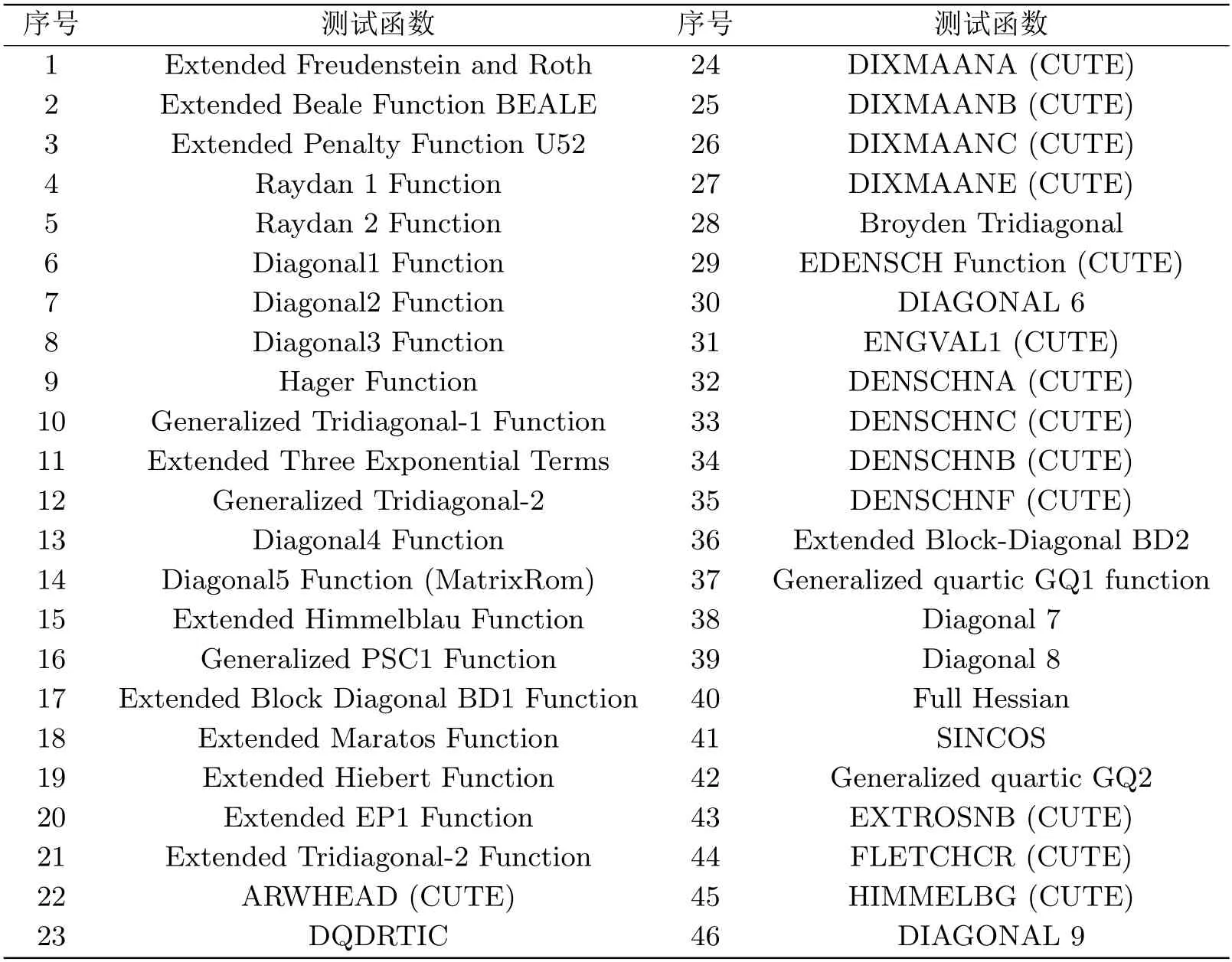
表1 测试函数

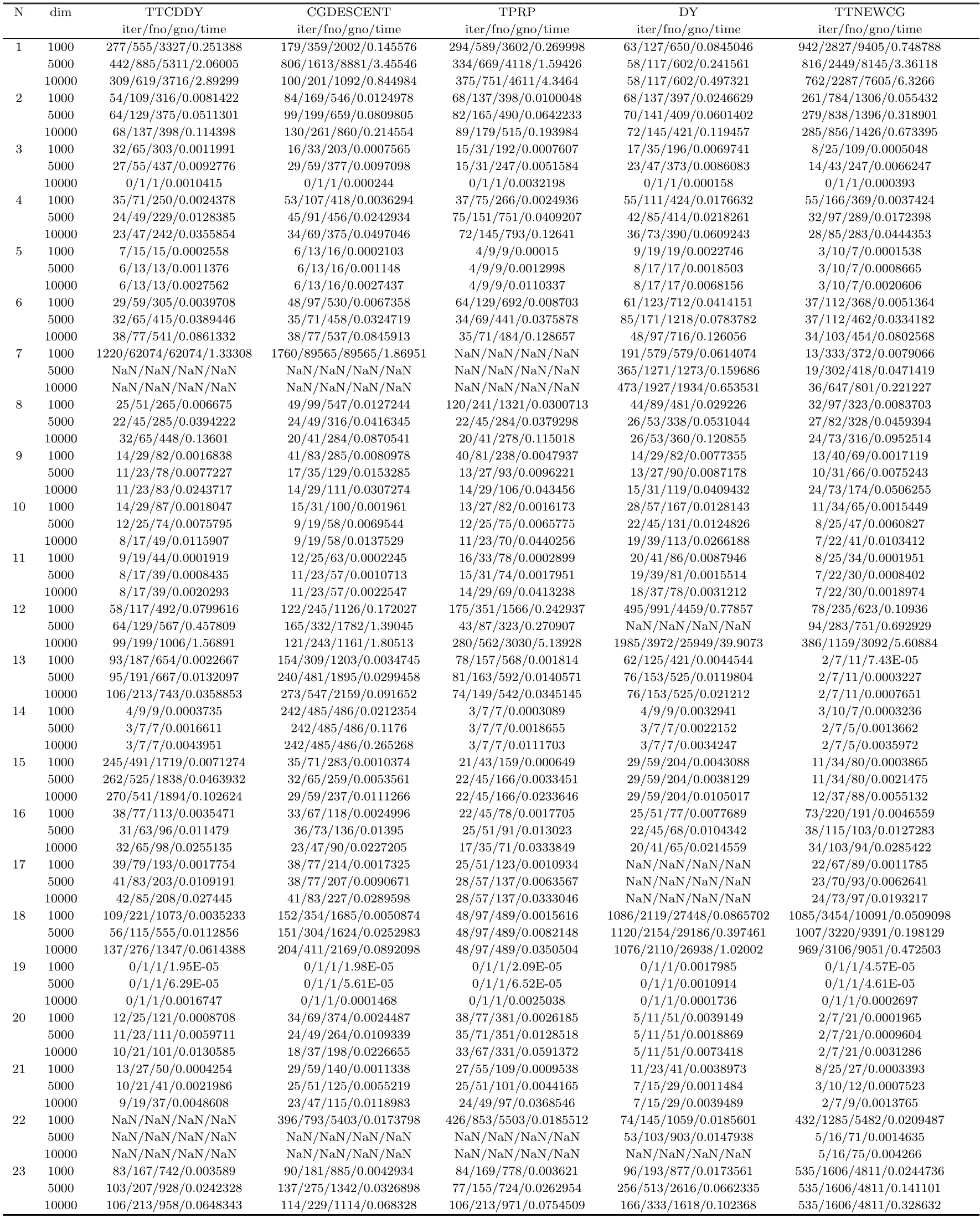
表2 算法数值结果

通过表2中138个测试问题的结果可知,算法TTNEWCG能够全部求解所有测试问题,由此可知算法TTNEWCG是有效的.

除了通过表格验证新算法的有效性和可行性外,本文将采用Dolan和Mor´e[25]性能图来更加直观的对比分析四个算法数值效果.下面是性能图原理的简单介绍.在实验环境相同情况下,四种算法求解同一个测试问题,这里有P代表由单个测试问题p组成的问题集合,S表示由单个算法s组成的集合.tp,s表示使用算法s求解测试问题p的耗费时间,性能比rp,s的数值越小表明算法s对于问题p的求解性能越好.rp,s计算表达式为:

ρs(τ)定义为性能分布函数,ρs(τ)的曲线越高,其对应方法的数值性能就越好计算,它的计算公式如下:

图1-4展示对比算法多维度解决138个测试问题的数值性能,其中最大维度达到10000.类似表2性能图中的Iter,Fno,Gno,Time分别代表算法迭代次数,目标函数迭代次数,目标梯度迭代次数和CPU运行时间.

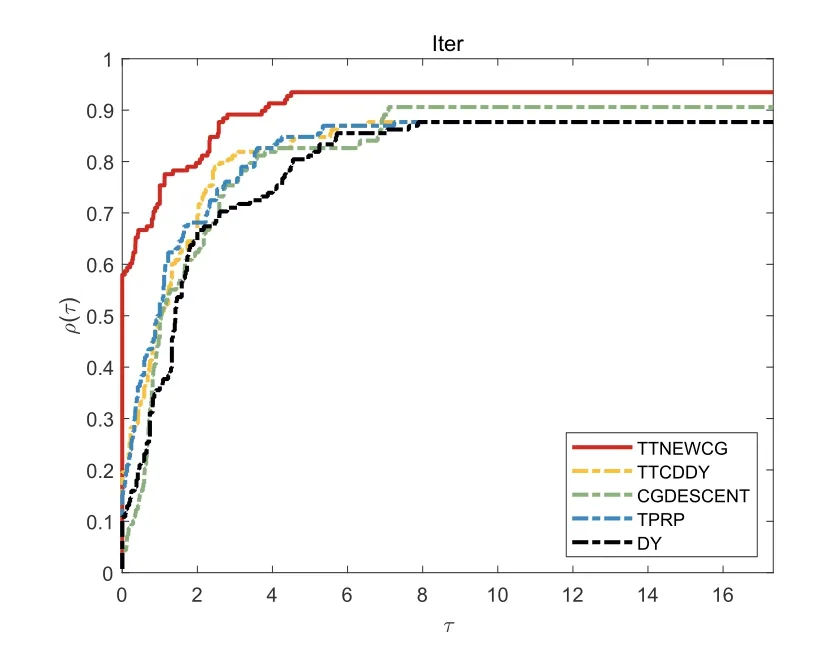
图1 算法迭代次数性能图

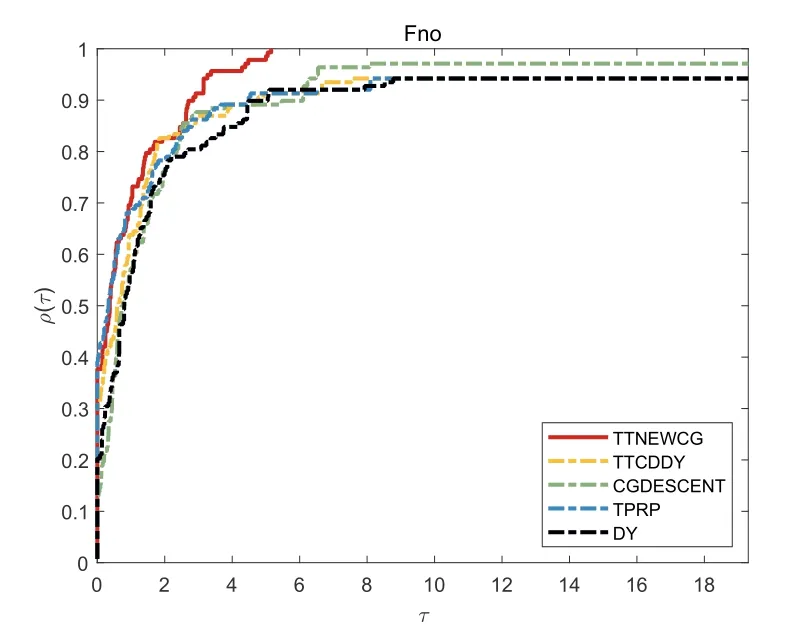
图2 目标函数迭代次数性能图

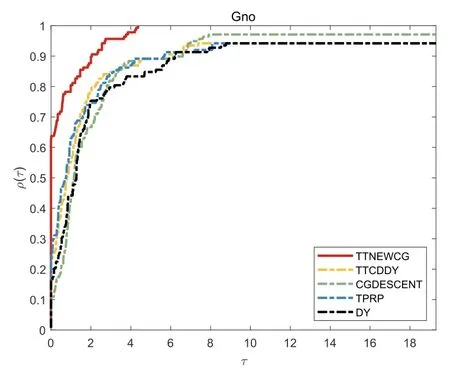
图3 梯度函数迭代次数性能图

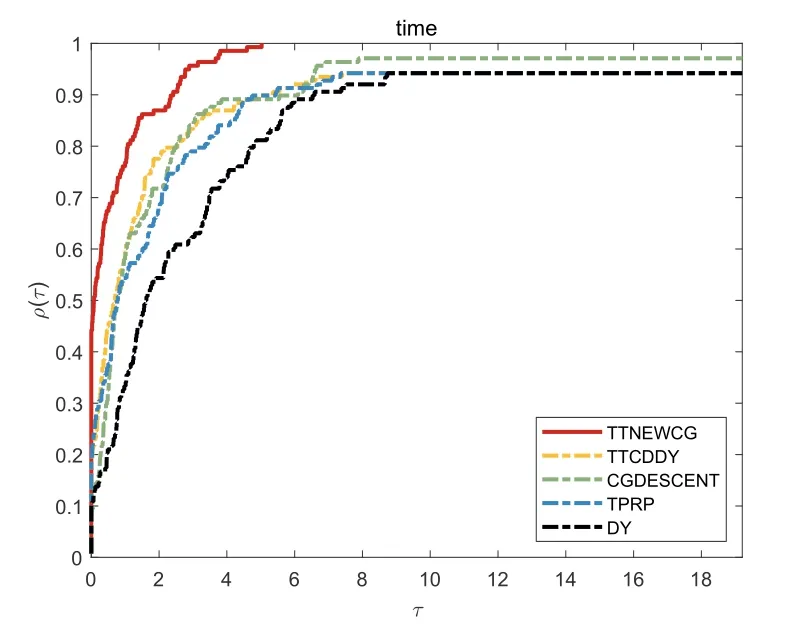
图4 CPU运行时间性能图

从性能图的特征可以知道,曲线越高,相应的方法越好.通过对比图1-4可知TTNEWCG算法在迭代次数、目标函数迭代次数、梯度函数迭代次数、CPU运行时间上的性能效果优于对比算法TTCDDY[19]、CGDESCENT[15]、TPRP[18]、DY[8].

对以上实验结果进行分析,TTNEWCG的良好效果主要取决于共轭参数的选择和搜索方向的改进.大多数方法中的共轭参数都是定值,而TTNEWCG新算法中的共轭参数是自适应的,计算参数上相比其他算法减少了计算量和存储,并且搜索方向接近BFGS方向,因此,TTNEWCG相比其他方法是有优势的.

5.结束语

为了更加有效的求解大规模无约束优化问题,本文基于自调比无记忆BFGS拟牛顿法,提出一个关于共轭参数DY的自适应双参数共轭梯度法,设计的搜索方向满足充分下降性,在一般假设和标准Wolfe线搜索准则下具有充分下降性和全局收敛性,数值实验结果证明新算法是有效可行的.