一种控制输入约束下的不确定离散系统非脆弱保性能控制器设计

段虹州 韩光信 高兴泉

摘 要：【目的】针对考虑扰动及摄动情况下的控制输入约束的不确定离散系统，提出了非脆弱保性能的控制方法。【方法】首先，以最小化目标函数为性能指标、控制输入饱和范围为约束条件，从而推导出约束状态下的非脆弱保性能控制律。其次，使用李雅普诺夫方程来构造非线性矩阵不等式。再次，结合Schur补定理和布谷鸟群智能优化算法对不等式进行求解，得到控制输入约束下的非脆弱保性能控制律的参数。最后，通过Quanser三自由度陀螺仪平台进行试验验证。【结果】试验结果表明，本研究所提出方法的稳态误差浮动不超过0.07、跟踪误差不超过0.15。【结论】该方法在面对扰动及摄动情况时具有更高的鲁棒性，对提升三自由度陀螺仪的稳定性及控制精度具有重要意义。

关键词：不确定性离散系统；控制输入约束；非脆弱性；保性能控制

中图分类号：TP273     文献标志码：A     文章编号：1003-5168（2024）03-0004-06

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.03.001

Non-Fragile Guaranteed Cost Control for Uncertain Discrete

System with Control input Constraints

DUAN Hongzhou1 HAN Guangxin1 GAO Xingquan1，2

（1.Jilin Institute of Chemical Technology， Jilin 132022，China;

2.Jilin Industrial Vocational and Technical College， Jilin 132013，China）

Abstract： [Purposes] In this paper， a non-fragile guaranteed performance control method is proposed for uncertain discrete systems with input constraints under perturbation. [Methods] In this method， By taking the minimum objective function as the performance index and taking the saturation range of the control input as the constraint condition， the non-fragile guaranteed performance control law under the constraint state is derived. Secondly ， the nonlinear matrix inequality is constructed by Lyapunov equation.  Then， Schur's complement theorem and Cuckoo bird intelligent optimization algorithm are used to solve the inequality， and the non-fragile guaranteed performance control law parameters under the control input constraints are obtained. Finally， the experiment is verified by Quanser-3-DOF gyroscope platform. [Findings] The results show that the steady-state error of the proposed method is less than 0.07 and the tracking error is less than 0.15. [Conclusions] The method proposed in this paper has higher robustness in the face of disturbance and perturbation， and is of great significance for improving the stability and control accuracy of the 3-DOF gyroscope.

Keywords： uncertain discrete system; control input constraint; non-fragile; guaranteed performance control

0 引言

非脆弱保性能控制［1］是指在控制系統中考虑输入约束和性能指标的前提下来设计控制律，从而使系统具有优异的性能，在面对不确定性或扰动时能保持强鲁棒性。该方法被广泛应用于工业生产［2］、机器人控制［3］、航空航天［4］等领域。

保性能控制起源于20世纪末，在21世纪得到进一步发展，学者们经过研究相继取得了诸多成果。Yu等［5］提出关于不确定离散系统的保性能控制方法；Chen等［6］提出不确定离散时滞系统的保性能控制方法；Fan等［7］提出连续时间系统的保性能控制方法；He等［8］提出不确定T-S模糊系统的保性能控制方法；Yang等［9］对离散线性系统的保性能控制进行深入研究。

Makila等［10］研究发现，若某些控制器的参数发生极其微小的波动，闭环系统的性能有可能会大幅度下降，严重时甚至会直接导致系统不稳定。因此，对自身参数摄动具有较强抵制能力的控制器被称为非脆弱控制器［11］。Jiang等［12］提出将H∞控制和非脆弱控制融合的办法，并进行了实践验证；Gao等［13］对非脆弱、保性能和H∞控制的融合进行研究。

上述研究成果并未考虑控制输入约束，获得的控制器参数通常具有较高的增益，易导致系统不稳定或设备损坏。因此，本研究考虑最小化性能函数、系统不确定性、控制输入约束及控制器增益摄动，提出了一种控制输入约束下的非脆弱保性能控制器设计方法，在保证系统运行能满足控制输入约束的同时，还具有良好的性能，并在三自由度陀螺仪上验证了所提方法的有效性。

1 问题描述

考虑不确定的离散系统表示见式（1）。

[x（k+1）=A+ΔAx（k）+B+ΔBu（k）x（0）=x0] （1）

式中：[x（k）∈Rn]为系统状态向量；[u（k）∈Rm]为控制输入向量；[ΔA]、[ΔB]為反映系统模型中参数不确定性的未知实矩阵。

本研究考虑参数不确定性时假设为范数有界，见式（2）。

[ΔAΔB=HFE1E2] （2）

式中：[H]、[Ei]（[i=1，2]）为具有合适维数的确定矩阵；[F]可测，且满足[FTF≤I]；[I]为具有适当维数的单位矩阵。上述参数反映出不确定参数的结构信息。

由于执行机构饱和因素，控制输入必须满足约束条件，见式（3）。

[uν（k）=eTvu（k）≤uν，max，ν=1，2，…，m，t>0] （3）

式中：uv为向量u的第[ν]个分量；[ev]为引入的空间[Rm]第[ν]个标准向量基。

考虑控制输入约束的非脆弱保代价控制问题描述如下。设计的状态反馈控制器见式（4）。

[u（k）=（K+ΔK）x（k）=Kx（k）] （4）

为使闭环系统内部稳定，最小化目标函数见式（5）。

[J=k=0∞xT（k）Qx（k）+uT（k）Ru（k）] （5）

同时，为满足控制输入约束，[Q]和[R]为给定的正定对称矩阵，[K]为设计的状态反馈控制器增益，[ΔK]为控制增益加性摄动，[M]和[N]为具有合适维数的确定矩阵，[Fk]可测且满足[FTkFk≤I]，[I]为具有适当维数的单位矩阵。

引理1：取[M=MT]，[H]和[E]为具有相应维数的实数矩阵，[F]满足[FTF≤I]，则以下条件等价［14］。

[M+HF（t）E+ETFTHT<0] （6）

存在标量[ε>0]，使得[M+εHHT+ε-1ETE<0]。

根据引理1，可推导出以下结论。

推论1：取[M=MT]，[H]和[E]为具有相应维数的实数矩阵，[Fi（t）]满足[FT（t）F（t）≤I]引理以下条件等价。

[M+HFE+ETFTHT>0] （7）

存在标量[ε>0]，使得[M-εHHT-ε-1ETE>0]。

若不等式[M+HF（t）E+ETFTHT>0]成立，则有[-M-HF（t）E-ETFTHT<0]，即[-M+（-H）F（t）E+ETFT（-H）T<0]，也即[M-εHHT-ε-1ETE>0]。

2 非脆弱保性能控制器设计

将控制器（4）代入到系统（1）中，并考虑系统模型的不确定性（2），得到的闭环系统见式（8）。

[x（k+1）=Aclx（k）x（0）=x0] （8）

式中：[Acl=A+HFE1+（B+HFE2）K]。

对于系统（8），若存在对称正定矩阵[P]使得[K]满足式（9）。

[ATclPAcl-P+Q+KTRK<0] （9）

则状态反馈控制律[u（k）=Kx（k）]是系统的一个具有性能矩阵[P]的保性能控制律。其中，[K=K+ΔK]，控制性能目标函数（5）的一个上界为[J*=xT0Px0]，即对所有的[k>0]，都有[xT（k）Px（k）≤xT0Px0]。

为消除不等式条件（7）中含有的模型不确定性，获得易检验条件，根据推导，得到保证式（4）成立且保证目标函数[J≤α]的充分条件，即存在标量[ε1>0]，对称正定矩阵[X=P-1]，使得以下矩阵不等式成立，见式（10）、式（11）。

该不等式虽消除了模型的不确定性，但还包含控制器的增益摄动，下面寻找一个满足式（10）的充分条件。

定义[Y=KX]，根据Schur补定理有式（12）。

考虑控制输入约束（3），闭环系统满足控制约束意味着应有式（13）。

[uTv（k）uv（k）≤u2v，max， t≥0， v=1，2，…，m] （13）

根据[uv（k）=eTv（Kx（k））]，可得式（14）。

[xT（k）KTeveTvKx（k）≤u2v，max] （14）

式中：[ev]为引入的空间Rm第[ν]个标准向量基。

根据前面的讨论，若式（8）、式（9）成立，则对任意的[k>0]，均有[xT（k）Px（k）≤xT0Px0=α]，即式（8）成立的一个充分条件是对所有的[x（k）]均满足式（15）。

[xT（k）KTeveTvKu2v，maxx（k）≤xT（k）Px（k）α] （15）

将[K=K+ΔK=K+MFkN]代入，则有式（16）。

[u2v，maxeTvKKTevPα+eTvM0Fk（t）0N+0NTFTk（t）MTev0≥0] （16）

根据推论1，上式成立的一个充要条件是存在标量[ε3>0]使得式（17）成立。

[u2v，maxeTvKKTevPα-ε3eTvM0eTvM0T-ε-130NT0NTT≥0] （17）

左右两边同时乘以[diagIαP-1I]，定义[Y=KX]，见式（18）。

[u2v，max-ε3eTvMMTeναeTvY0αYTevXαXNT0αNXε3I≥0] （18）

假设初始状态范数[x0]有界，即[x0≤ψ]，则式（11）成立的一个充分条件见式（19）。

[1ΨIIαX≥0] （19）

3 基于布谷鸟算法的控制器参数整定

最小化矩阵不等式（19）求出性能指标的一个上界[?min=α]、满足控制输入约束（18）、存在一个P使（12）成立，并求出尽可能大的控制器参数[K1K2K3K4]。适应度函数的选择应以快速、准确为目标，使用ITAE误差为性能评价指标，见式（20）。

[?=0tτ·|e（τ）|dτ] （20）

式中：积分区间为系统仿真时间；[e]为实际输出和期望输出的差值。

布谷鸟算法流程为初始化、循环、最优解输出。

①初始化。设巢穴个数[N=4]、种群规模[D=25]，初始化巢穴的位置见式（21）。

[P0=x1（0）x2（0）x3（0）x4（0）T] （21）

②循环。在初始化及每次循环体结束后进行位置更新，保留上一次最优巢穴的位置[Pb（t-1）]对巢穴位置的更新见式（22）。

[xm（t+1）=xm（t）+σ?Levy，m=1，2，3，4] （22）

式中：[Levy?u=t-1-β（0<β≤2）]。

选取[0.25]作为巢穴主人发现寄生鸟蛋的可能性，并与[Pa]进行比较，并随机更新被发现概率较高的巢穴位置，得到一组新的巢穴位置，用新的、较好的巢穴代替原来较差的，得到一组新的巢穴位置，见式（23）。

[Pt=x1tx2tx3tx4tT] （23）

③最优解输出。找到前面环节得到的最优巢穴位置和最优解，若达到循环条件则停止迭代，此时输出最优解，见式（24）。

[K1K2K3K4=Pb=x1tx2tx3tx4tT] （24）

反之，程序跳转循环体继续进行迭代。

4 仿真分析与试验验证

本研究使用三自由度陀螺仪平台来验证文中所提方法的有效性。其动力学模型［15］见式（25）。

[J3q2 + P1cosq2q3 -Jαsinq2cosq2q23 = τ2]

[J2+Jasin2q2q3-P1cosq2q2+2Jasinq2cosq2q2q3][=0] （25）

利用前向差分定理将其离散化，得到不确定性离散系统，见式（26）。

[x（k+1）=AC+ΔAx（k）+BC+ΔBu（k）x（0）=x0]

（26）

式中：[AC=10-0.004hJy001000.004hJz0100001 ]；[BC=0.004Jy000]；[ΔA=r1A1]；[ΔB=r2B2]。

取[|r1|≤1]、[|r2|≤1]，取值通过放大转子质量至原来的1.1倍得到。控制输入约束为[|u（t）|≤5]。系统描述见式（27）。

[x（k+1）=AC+HFE1x（k）+BC+HFE2u（k）] （27）

对性能指标式（5），取[Q=200001600000.0100000.000 1]、[R=5]，经布谷鸟算法迭代200次，得到相对最小化。

性能指标[α=3.107 5]，此时对应的控制参数为K1=0.505 183 3，K2=1.172 301 764，K3=0.046 237 9，K4=0.000 084。

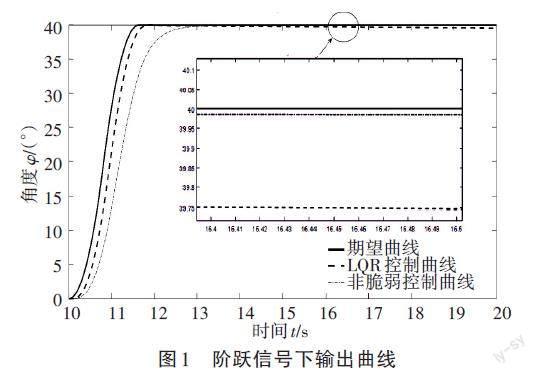
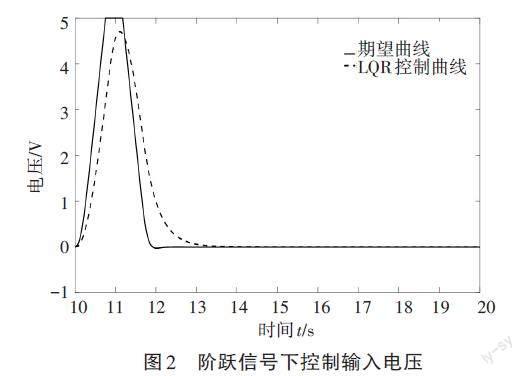
通过仿真试验来验证控制参数的准确性及控制效果。阶跃信号下输出曲线、输入电压如图1、图2所示，阶跃输入仿真控制精度见表1。

由表1可知，LQR控制方法的跟踪误差为0.392 2，优于非脆弱控制下的跟踪误差。LQR控制方法的稳态误差为0.32，远大于非脆弱控制下的跟踪误差。达到稳态后，非脆弱控制器可稳定控制系统运行，效果远强于LQR控制器。符合控制器设计思路，可进行实物验证。

考虑到模型内部干扰，将电机效率调至95%作为内部扰动，模拟电路老化导致的性能下降。考虑内部扰动的阶跃信号情况下输出电压、控制输入电压如图3、图4所示。

非脆弱保性能控制下的输出曲线响应速度较慢，稳态后，精度比LQR控制下要高。在设备运行时，非脆弱保性能控制始终未达到设定的电压上界，但LQR控制在每一次设备进行姿态变换时都超过临界值（5 V），有可能对设备造成损害。

将陀螺仪外部银色框架拧至轻微松动作为震动干扰，阶跃信号下输出电压如图5所示。

在同样的外部扰动情况下，非脆弱保性能控制的鲁棒性能相对突出，稳态误差为0.087 1。在外部扰动情况下，非脆弱保性能控制器的鲁棒性能要优于LQR控制器的鲁棒性能。

考虑控制器增益摄动，设非脆弱控制器为[K]，但实际上执行的控制见式（28）。

[K=s1ΔK1+s2ΔK2] （28）

式中：[ΔK1=10]；[ΔK2=01]；[-1≤s1（t）≤1]；[-1≤s2（t）≤1]。

定义矩阵[Fk=diags1（t）s2（t）]，则控制器增益的描述见式（29）。

[ΔK=MF（t）N] （29）

式中：[M=11]；[N=1001]，取[Ψ=π24]代入式（23）。

考虑控制器摄动的阶跃信号情况下输入电压、控制输出电压如图6、图7所示。

5 结语

本研究基于最小化性能函數、控制输入约束、保性能控制等需求来设计控制器，通过李雅普诺夫方程推导将其转化为成立的充分条件，进而推导出非线性矩阵不等式，再使用布谷鸟群智能优化算法对其进行求解优化。通过仿真试验来验证其可行性，再将求得的控制器带入三自由度陀螺仪平台中。试验结果表明，约束状态下存在允许范围内的扰动或摄动，本研究所提出的非脆弱保性能控制器具有更好的鲁棒性及控制精度。

参考文献：

［1］WU M，LAN Y H，SHE J H，et al. Design of non-fragile guaranteed-cost repetitive-control system based on two-dimensional model［J］.Asian Journal of Control： Affiliated with ACPA，the Asian Control Professors' Association，2012（1）：109-124.

［2］KONG Y S，ZHAO D X，YANG B，et al.Robust non-fragile H-infinity/L-2-L-infinity control of uncertain linear system with time-delay and application to vehicle active suspension［J］.International Journal of Robust and Nonlinear Control，2015（13）：2122-2141.

［3］SUN P，WANG S Y.Guaranteed cost non-fragile tracking control for omnidirectional rehabilitative training walker with velocity constraints［J］.International Journal of Control，Automation and Systems，2016（5）：1340-1351.

［4］WANG Y F，JIANG C S，WU Q X.Multi-model soft-switching cost-guaranteed non-fragile control for near-space vehicle［J］.Control Theory & Applications，2012（4）：440-446.

［5］YU L ，GAO F R.Optimal guaranteed cost control of discrete-time uncertain systems with both state and input delays［J］.Journal of the Franklin Institute，2001（1）：101-110.

［6］CHEN W H，GUAN Z H，LU X .Delay-dependent guaranteed cost control for uncertain discrete-time systems with delay［J］.IEE Proceedings - Control Theory and Applications，2003（4）：412-416.

［7］FAN Q Y，YANG G H.Adaptive nearly optimal control for a class of continuous-time nonaffine nonlinear systems with inequality constraints［J］.Isa Trans，2017，66：122-133.

［8］HE M，LI J M .Robust nonfragile guaranteed cost control for uncertain T-S fuzzy Markov jump systems with mode-dependent average dwell time and input constraint［J］.International Journal Of Systems Science，2018（13-16）：3146-3168.

［9］YANG X，LIU S J.Optimal control of unknown discrete-time linear systems with additive noise［J］.Journal of Systems Science and Complexity，2023（2）：591-612.

［10］MAKILA P M，KEEL L H，BHATTACHARYYA S P.Comments on Robust，fragile，or optimal？ ［with reply］［J］.IEEE Transactions on Automatic Control，1998（9）：1265-1268.

［11］FATEME B，VALIOLLAH G，MANUEL S.Non-fragile robust model predictive controller design for uncertain time-delay systems with input constraints［J］.2023（6）：1259-1274.

［12］JIANG X L，XIA G H，FENG Z G，et al.Non-fragile guaranteed-performance H ∞ leader-following consensus of Lipschitz nonlinear multi-agent systems with switching topologies［J］.Nonlinear Analysis Hybrid Systems，2020（3）：100913.

［13］GAO X Y，TEO K L，DUAN G R.Non-fragile robust H∞ control for uncertain spacecraft rendezvous system with pole and input constraints［J］.International Journal of Control，2012（7）：933-941.

［14］XIE L H.Output feedback H∞ control of systems with parameter uncertainty［J］.International  Journal of Control，1996（4）：741-750.

［15］劉志成.基于三步法的三自由度陀螺仪轨迹跟踪控制［D］.吉林：吉林化工学院，2022.