采摘机器人的定位和轨迹预测算法研
——基于大数据技术究
聂恒志,吴 升,张 璐
(1.福州大学 数字中国研究院(福建),福州 350003;2.河南工业职业技术学院,河南 南阳 473000)
0 引言
采摘机器人是一个复杂的系统,需要具备环境检测、指令分析和执行动作等功能。随着信息化技术的发展,采摘机器人的功能更趋向于多样化,人们对其要求也越来越高。采摘机器人自主作业需要对自身位置和运动轨迹进行预测,故本文设计了基于大数据技术的采摘机器人定位和轨迹预测算法。
1 建立采摘机器人运动学模型
1.1 采摘机器人运动学分析
为了实现对采摘机器人定位和轨迹预测,采用世界坐标系XOY建立运动学模型,如图1所示。
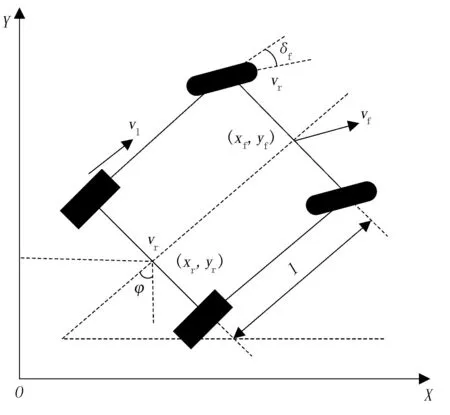
图1 采摘机器人运动学模型Fig.1 The kinematics model of picking robot
图1中,采摘机器人前后轮轴间中心的坐标为(xf,yf)和(xr,yr),前轮偏向角和航向角分别为δf和φ,其他参数如表1所示。

表1 采摘机器人运动学参数表
为了减少计算量,做如下假设:
1)采摘机器人的运动为刚体运动;
2)采摘机器人在运动过程中,其前后轮偏向角保持一致,由舵机控制;
3)采摘机器人在转弯过程中,转弯半径等同于道路曲率半径。
1.2 采摘机器人运动学分析
对采摘机器人的后轮轴进行分析,后轮轴中心坐标(xr,yr)沿着线速度方向进行分割,其表达式为
(1)
对采摘机器人的前轮轴进行分析,可以求出其约束条件为
(2)
结合采摘机器人航向角φ和前后轴间距,可以计算出前后轴两个轴中心之间的数学关系,再对其进行求导可得
(3)
将式(1)、式(3)代入式(2),并对其进行三角函数展开求解,可得采摘机器人的角速度表达式为
ω=vrtanδf/l
(4)
再对采摘机器人航向角φ进行求导,便能计算出采摘机器人的角速度。联立式(1)和式(4),可得
(5)
采用以上方法可以搭建该采摘机器人的控制系统,其输入量和实时状态量表达式分别为u=[vrδf]T和ξ=[xryrδf]T。
1.3 运动分析的线性误差模型
对式(5)进行线性化处理,假设ξref为期望的状态值,那么对于其中任意的期望状态都会满足以下表达式,即
(6)
展开ξ在期望处的一阶泰勒表达式为
(7)

(8)
采用雅可比矩阵对式(8)的系数矩阵进行求解,并分别用A和B表示,可以得到线性误差模型为
(9)
1.4 运动模型离散化
对式(9)进行离散化处理,可得
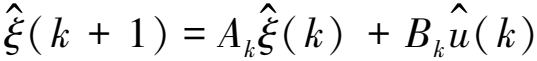
(10)
其中,T为数据采样时间。
采摘机器人控制系统的定义输出为
(11)

(12)
(13)
以上是对采摘机器人的运动学分析,同时结合神经算法和定位系统,便可以实现对采摘机器人的定位和轨迹预测。
2 与大数据融合的神经网络模型
2.1 神经网络原理
神经网络是一个通过获取知识和保存知识来模拟人大脑的运算模型,由大量的相互突触(或称“神经元”)和之间相互的联接构成,每个突触代表一定的输出函数,被称为激励函数,而突触之间的连接则代表通过连接信号的加权值。
神经网络是一种多层前馈式网络,具体的工作原理为:通过对输入和输出值进行比较,计算出详细的误差值,并对其前导层的误差进行估计;然后,用该误差对更前一层的计算误差进行推导,再依次进行反转,求出各层之间的误差估计。其具体的网络结构如图2所示。
神经网络包括输入、隐含和输出3个层级,两两层级间的神经元都相互存在关系,但同一个层级间的神经元却没有任何联系。假设神经网络有L层,除去输入层的神经元,还存在N0个,第L层有NK个元,那么其输入和输出的关系表达式为
(14)
其中,uk(i)为第K层第i个神经元接收上一层的信息;wk(i,j)为从第k-1层第j个神经元元到第k层第i个神经元元的权值;ak(i)为第k层第i个元的输出值。
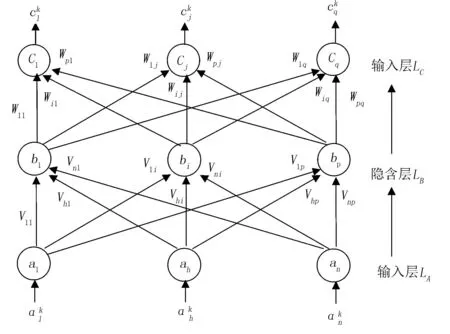
图2 神经网络结构图Fig.2 The structure diagram of neural network
神经网络算法的流程为:
Step1:选择合适的初始学习数据集p=1,…,p,并设定初始权矩阵为W(0)。
Step2:利用初始学习数据集计算网络输出。
Step3:用式(14)对计算结果进行反向的修正,直到对所有数据都完成学习,再输出结果。
2.2 神经网络融合模型
随着人工智能的快速发展,涌现出了大量大数据应用服务。大数据Hadoop的核心技术包括Map和Reduce。其中,MapReduce是对键值对进行处理,而Map则是对输出数据进行处理,并生成键值对格式的中间数据;然后,利用密钥对这些数据进行排序和分区处理,并在Reduce阶段将相同的键值对进行聚合,方便后级模块进行分析处理。在此,采用大数据Hadoop技术对神经网络的输入数据进行分割、映射、排序、合并、分类等操作,再利用神经网络对采摘机器人的位置和轨迹进行分析。
为了可靠和准确地对采摘机器人进行定位和轨迹预测,利用GPS定位模块和深度神经网络(Deep NeuralNetworks,DNN),将其与大数据进行多元信息融合,建立了神经网络融合模型。将采摘机器人运动速度、角速度、偏航角、定位数据、转向角和道路曲率作为神经网络融合模型的输入,并利用该模型对输入数据、模型训练和测试进行预测。神经网络融合模型包括数据处理、信息搜集和结果融合3个模块,模型采用大数据和DNN技术融合的预测方法构建复杂方程的采摘机器人运动模型,实现对采摘机器人位置的定位和轨迹预测功能。
将经过大数据Hadoop处理后的输入数据归一化处理在[-1,1]范围内,再将这些信息反映到共同的描述空间,输入给DNN网络,并通过完全连接层对隐含层数据进行输出。该模型架构如图3所示。

图3 神经网络融合模型结构图Fig.3 The structure diagram of neural network fusion model
将数据送到输出层进行预测,然后根据1、2、3s的时间对采摘机器人的轨迹进行预测。模型融合层的计算表达式为
e=tanh(Wf[hDNN;hHadoop]+bf)
(15)
其中,hDNN为DNN的隐藏层;hHadoop为大数据处理模式;Wb和bf为学习模型的参数;e为融合层的输出。
神经网络融合模型训练中的损失函数采用GPS定位到的真实位置和预测轨迹之间的均方误差(Mean Square Error,MSE)表示,即
(16)
其中,yt和Pt分别为t时刻GPS定位到的真实位置和模型预测的位置值;T为整体的时间。这样就完成了大数据和DNN技术的融合,实现了神经网络融合模型。
2.3 DNN网络设计
将DNN技术应用到采摘机器人轨迹预测时,可以通过对其作业环境和作业模式进行训练,在离线过程中通过对之前采集的数据进行训练,实现对轨迹的准确预测。为了提高整个系统轨迹预测的准确性,神经网络融合模型采用离线模式,大数据来源包括行驶在各种道路曲率的作业数据。数据从输入层和多层的隐藏层后从输出层出来,数据在各个层间处理传输时需要乘以权重,而隐藏层则需要通过激活函数处理后传输到下个层级。神经网络融合模型是为了实现对采摘机器未来横向运动的预测,故采用带泄露修正线性单元(Leaky Re LU)激活函数,其定义为
(17)
其中,λ为常数,取λ=0.2。
DNN成本函数可以将输入和输出的数据作为输入进行成本C的计算,其表达式为
(18)

为了实现DNN计算成本的最小化,采用梯度下降对DNN各层的权重进行更新,即
(19)
其中,α和Wi分别为DNN模型的学习率和t时刻的权重。
最后,采用均方根反向传播对DNN模型进行优化。该算法采用变量M(w,t0)对前一段时间梯度平方的平均值进行保存,然后实现DNN学习率的自适应调整。其表达式为
(20)
其中,w和t0分别为DNN的工作权重和训练步骤;∂E/∂wt0为训练步骤t0中w的梯度。
DNN模型的输入包括采摘机器人运动速度、角速度、偏航角、定位数据、转向角和道路曲率;输出层包括6个节点,分别对应后续对1、2、3s对采摘机器人的纵向和横向预测;模型采用Leaky Re LU激活函数;网络隐藏层设置为5层,神经元设置为320,数据量为2560,学习率设置为0.1,迭代次数设置为200次。
3 仿真实验分析
为了评估对采摘机器人定位和轨迹预测的准确性,基于MatLab仿真软件采用DNN融合模型对采摘机器人轨迹1、2、3s 处的纵向预测和横向预测进行预测,系统使用80%的数据用于训练,20%的数据用于测试。用于仿真的道路轨迹和仿真结果分别如图4和图5所示。

图4 用于仿真的道路轨迹Fig.4 The road trajectory for simulation

图5 仿真结果Fig.5 The simulation result
由仿真结果可以看出:模型对采摘机器人的预测精度较高,误差在允许范围内,预测精度从高到低依次为1、2、3s。后续可以再增加数据量,会对时间长的预测轨迹有改善。这表明,该模型用于采摘机器人的定位和轨迹预测具有一定的可行性。
4 结论
为了实现采摘机器人的自动驾驶,将深度神经网络和大数据技术进行多元信息融合,将采摘机器人的运行信息作为模型输入参数,实现对采摘机器人的定位和轨迹预测。仿真结果表明:模型对采摘机器人的预测精度较高,误差在允许的范围内,具有一定的可行性。

