再谈三角形内切圆的几个性质及应用

●沈文选 (湖南师范大学数学奥林匹克研究所 湖南长沙 410081)

再谈三角形内切圆的几个性质及应用

●沈文选 (湖南师范大学数学奥林匹克研究所 湖南长沙 410081)

笔者在文献［1］中介绍了三角形内切圆的几个性质及应用，以下是笔者再次给出的几个性质及应用．

性质7设△ABC的内切圆分别切边BC，CA，AB于点D，E，F，记以A为圆心，AE为半圆的圆为W，直线DE交圆W于点G，点H在圆W上，则GH为圆W的直径的充要条件是H，F，D三点共线．

证明如图1，注意到△AEG和△CED均为等腰三角形，且底角相等，则知其顶角相等，即

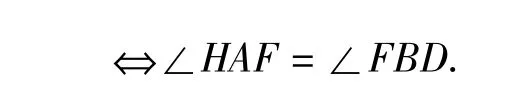
注意到△AHF和△BDF均为等腰三角形⇔其对应底角相等，即∠AFH=∠BFD⇔H，F，D三点共线．

推论3设△ABC的内切圆分别切边BC，CA，AB于点D，E，F，直线DE，DF分别交过点 A且与BC平行的直线于点G，H，直线AD交内切圆于点L，则 AG=AH，且∠GDH+∠GLH=180°．

事实上，由AE=AF并注意到图中的等腰三角形可得AG=AH;由∠GAL=∠LDB=∠LED知A，L，E，G 四点共圆，于是∠ALG=∠CDG．同理可得∠ALH=∠BDH，由此即可得

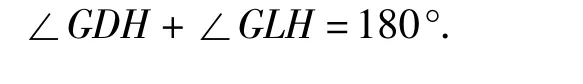
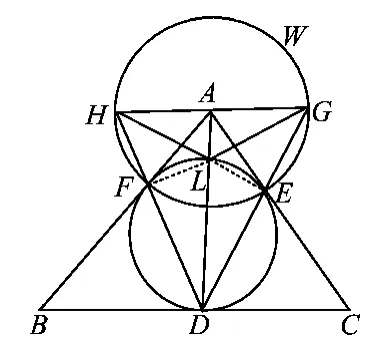
图1

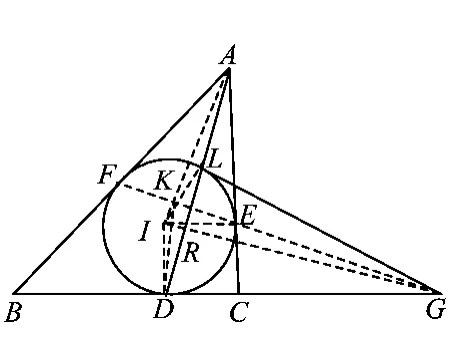
图2

由式(1)，式(3)可知，G，E，F 三点共线．

必要性当G，E，F三点共线时，如图2，连结GI交DL于点R，则IR⊥DL．

类似于充分性证明．由FI2=ID2=IR·IG，可证得 F，I，R，E 四点共圆．又 A，F，I，E 四点共圆，得∠IRA=∠IEA=90°，从而 IR⊥AR，故 A，L，D 三点共线．

性质9设△ABC的内切圆为⊙I，点D，E，F依次为⊙I上3个点(点D在优弧上，且与点A，I不共线)，EF与AI交于点K，且K为EF的中点，则E为AC与⊙I的切点(或F为AB与⊙I的切点)的充要条件是△IDK∽△IAD．

证明如图3，显然AI⊥EF．

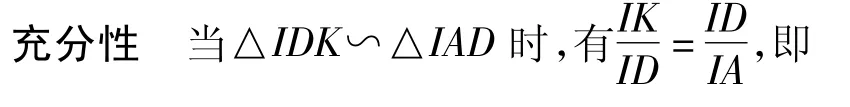
注意到∠EIK公用，得△IEK∽△IAE，即∠IEA=∠IKE=90°，因此 AE与⊙I切于点E，且AE为过定点与⊙I右侧相切的直线，而这样的直线是唯一的，于是E为AC与⊙I相切的切点．

同理可得，F为AB与⊙I的切点．

必要性当E为AC与⊙I的切点时，则由对称性(即K为EF中点)知点F必为AB与⊙I的切点，反之亦真．此时，显然有式(2)，即△IDK∽△IAD．

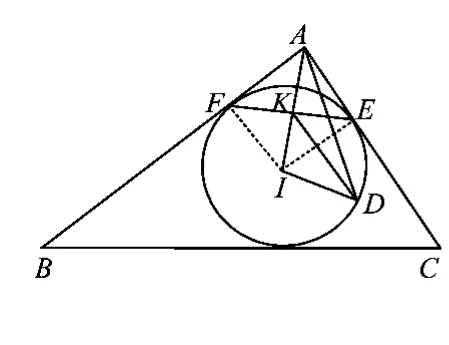
图3

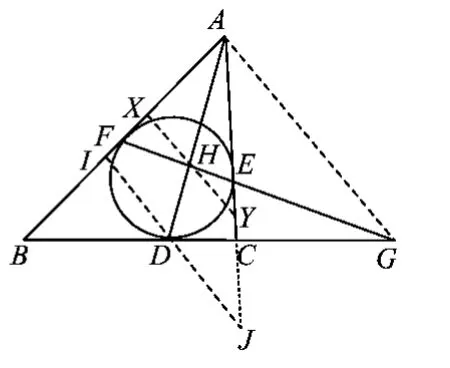
图4

推论4设△ABC的内切圆分别切边BC，CA，AB于点D，E，F，直线AD交内切圆于点L，过点L作内切圆的切线分别与直线DF，DE，BC交于点S，T，G，则

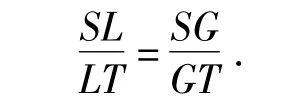
证明如图5，由性质8，知F，E，G三点共线．设直线AD与EF交于点H，则由性质10知

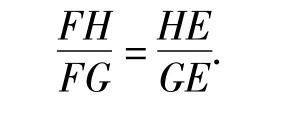
过点H作XY∥BC交直线DF于点X，交直线DE于点 Y，则

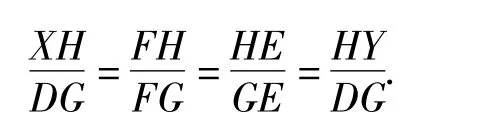
由上即知点H为XY的中点，过点L作IJ∥XY交直线DF于点I，交直线DE于点J，则知点L为IJ的中点，即 IL=LJ，于是

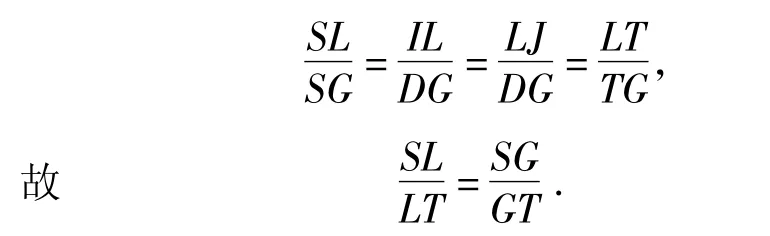
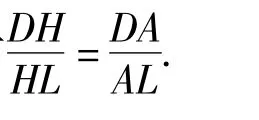
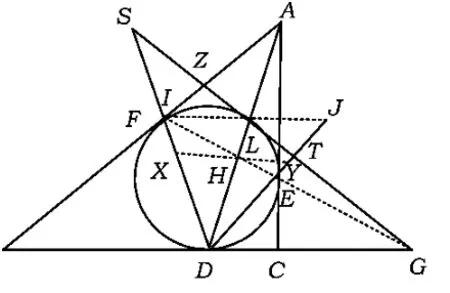
图5

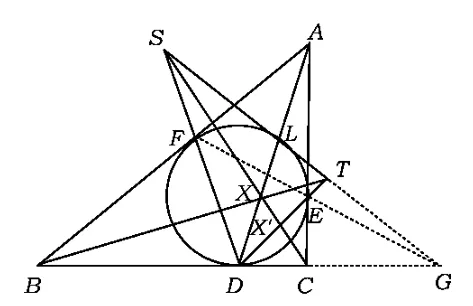
图6

推论5设△ABC的内切圆分别切边BC，CA，AB于点D，E，F，连结AD交内切圆于点L，过点 L作内切圆的切线分别与直线DF，DE交于点S，T，则直线AD，BT，CS共点．

证明当ST∥BC时，可知△ABC为等腰三角形，此时结论显然成立．

当ST与BC不平行时(如图6)，可设直线ST与直线BC交于点G，于是由性质8知F，E，G三点共线．

由性质10证明中的式(4)，可知

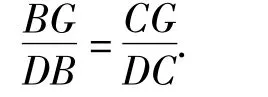
又由推论4，知

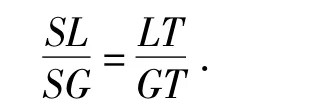
设BT交AD于点X，CS交AD于点X'，则对△DGL及截线BXT、对△DGL及截线CX'S分别应用梅涅劳斯定理，得

由上式知点X与X'重合，故直线AD，BT，CS共点．

注性质10及推论4中的结论，应用线段的调和分割性质证明更为简捷．

性质11设△ABC的内切圆⊙I分别切边BC，CA于点D，E，直线 DI交⊙I于另一点 P，直线AP交边AB于点Q，点S在边AC上，BC与AQ交于点L，则SC=AE的充要条件是AP=LQ．

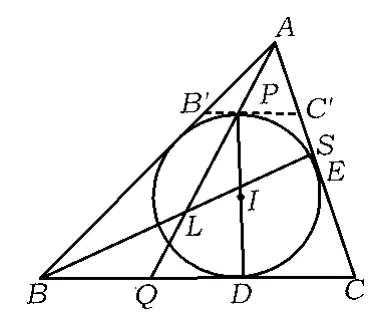
图7

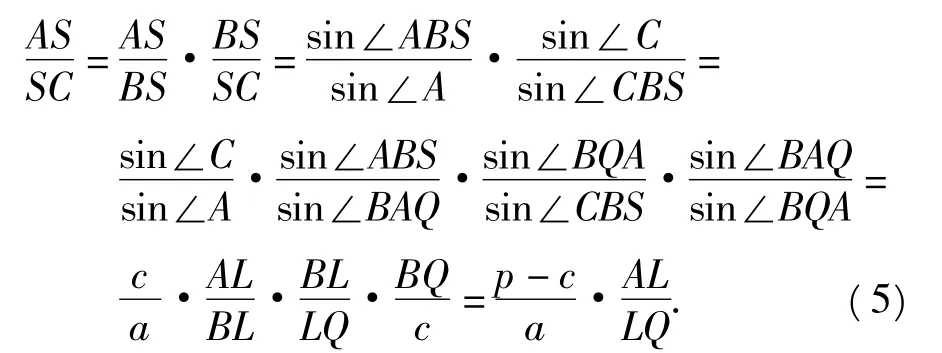
过点P作B'C'∥BC交AB于点B'，交AC于点C'，则 B'C'为⊙I的切线．设 r，rA分别为△AB'C'与△ABC在∠BAC内的旁切圆半径，S△为△ABC的面积，则

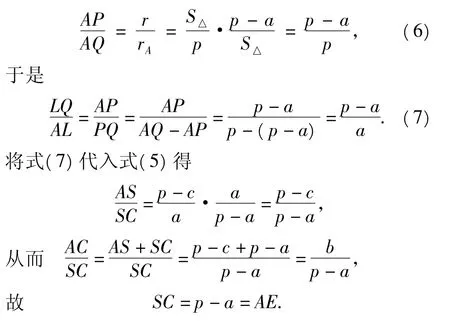
必要性当SC=AE时，SA=CE，对△AQC及截线BLS应用梅涅劳斯定理，得

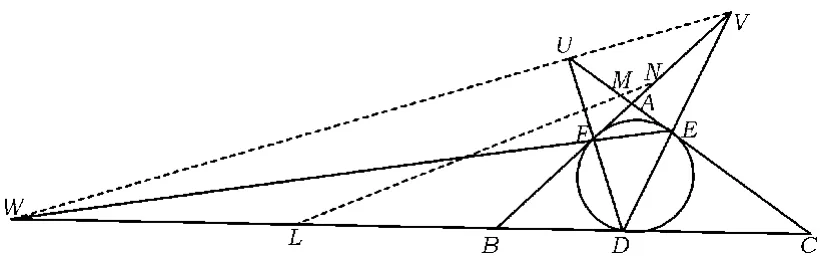
图8

性质12设△ABC的内切圆分别切边BC，CA，AB 于点 D，E，F，直线 FD，DE，EF 分别与直线CA，AB，BC 交于点 U，V，W，则 U，V，W 三点共线．

证明 若 FE∥BC，则视 W为无穷远点;当UV∥BC时，也视U，V，W三点共线．

当FE与BC不平行时，如图8．分别对△AFE及截线WBC、对△BDF及截线UAC、对△DCE及截线VAB应用梅涅劳斯定理，得

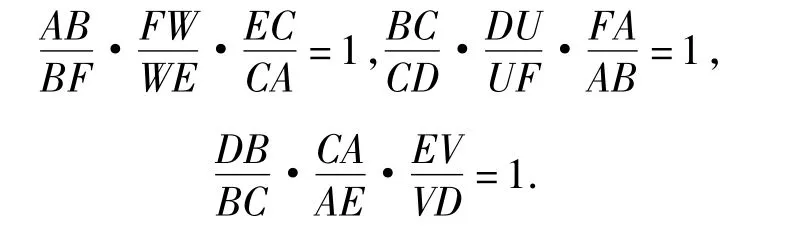
注意到AF=AE，BF=BD，CD=CE，上述3个式子相乘，得对△DEF应用梅涅劳斯定理的逆定理，知U，V，W三点共线．

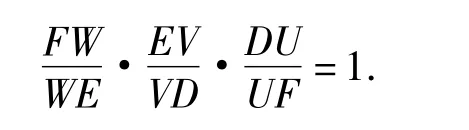
注U，V，W三点所在的直线称为勒莫恩(Lemoine)线．

下面介绍几个应用的例子．

例1已知△ABC的内切圆W分别切边BC，AC 于点 D1，E1，D2，E2分别在 BC，AC 上，且 CD2=BD1，CE2=AE1．记 AD2与 BE2的交点为P，圆W 与AD2相交点中离A较近的点为Q，求证:AQ=D2P．

(2001年第30届美国数学奥林匹克竞赛试题)

证明如图9，设圆W的圆心为I．因为CD2=BD1，所以由性质 5，知 D1，I，Q 三点共线．再由性质11，知当 CE2=AE1时，AQ=D2P．

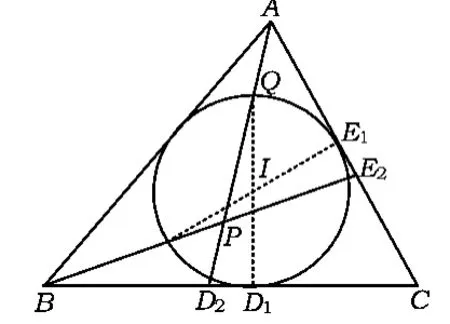
图9

图10

例2设I是△ABC的内心，且⊙I与AB，BC分别切于点X，Y，XI与⊙O交于另一点T，X'是AB与CT的交点，L在线段X'C上，且X'L=CT．证明:当且仅当A，L，Y三点共线时，AB=AC．

(2003年第20届伊朗数学奥林匹克竞赛试题)

证明如图10，设直线AL交BC于点Y'．由性质11，知当 X'L=CT 时，BY'=CY．于是 A，L，Y 三点共线，即Y'与Y重合，Y为BC的中点，从而AB=AC．

例3设△ABC是非等腰三角形，其内切圆为圆Γ，圆Γ与3条边BC，CA，AB分别切于点D，E，F．若 FD，DE，EF 分别与 CA，AB，BC 交于点 U，V，W，DW，EU，FV的中点分别为 L，M，N．证明:L，M，N三点共线．

(2008年印度国家队选拔竞赛试题)

证明如图8，由性质12知，U，V，W 三点共线．在四边形 VUFE中(或完全四边形 VUWFDE中)，应用牛顿线定理，即知L，M，N三点共线．

例4设△ABC是非等腰非直角三角形，设点O是它的外接圆圆心，并且 A1，B1，C1分别是边BC，CA，AB的中点，点 A2在射线 OA1上，使得△OAA1∽△OA2A，点B2和C2分别在射线 OB1和OC1上，使得△OBB1∽△OB2B和△OCC1∽△OC2C．证明:直线 AA2，BB2，CC2共点．

(1995年第24届美国数学奥林匹克竞赛试题)

证明如 图 11，由 △OAA1∽ △OA2A，△OBB1∽△OB2B，△OCC1∽△OC2C 及性质9，知A2B与⊙O相切于点 B，A2C与⊙O相切于点C，B2C，B2A，C2A，C2B 分别与⊙O 相切于点 C，A，A，B，于是⊙O是△A2B2C2的内切圆，切点分别为A，B，C．由切线长定理及应用塞瓦定理，知 AA2，BB2，CC2三线共点．

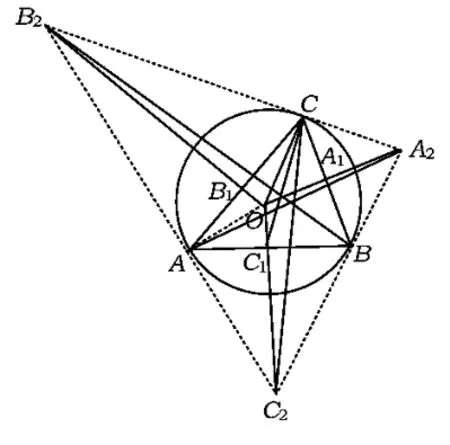
图11

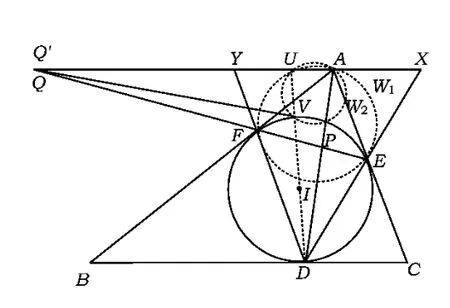
图12

例5在△ABC中，∠B≠∠C，△ABC的内切圆⊙I与 BC，CA，AB 的切点分别为 D，E，F，记 AD与⊙I的不同于点D的交点为P．过点P作AD的垂线交EF于点Q，X，Y分别是AQ与直线DE，DF的交点．求证:A是线段XY的中点．

(2006年第16届韩国数学奥林匹克竞赛试题)

证明如图12，记过点A且平行于BC的直线与过点P且与AD垂直的直线交于点Q'，直线DI与AQ'交于点U，直线PQ'与⊙I交于点V(V≠P)．由∠VPD=90°，知 D，I，V，U 四点共线．由∠BDI=90°，知∠AUI=90°．又∠AFI=90°= ∠AEI，知 A，F，I，E，U 五点共圆，记此圆为 W1．又由∠APV=90°=∠AUV，知 A，P，V，U 四点共圆，记此圆为 W2．注意到⊙I，圆W1，圆 W2两两相交的根轴 EF，PV，AU相交于一点(由∠B≠∠C知圆W1，圆W2，⊙I的圆心不共线)，而EF与PV相交于点Q，直线AU与PV交于点Q'，故Q与Q'重合，即QA∥BC．于是由推论3，知AX=AY，故A是线段XY的中点．

例6设⊙I为△ABC的内切圆，切边BC于点D，AB＞AC，连结 AD交⊙I于点 E，在 DE上取点F，使得 CF=CD，延长 CF交 BE于点 G，则 GF=FC．

(2008年中国国家代表队选拔赛试题)

证明如图13，设⊙I分别切边AB，AC于点P，Q，过点E的切线与直线BC交于点K．由性质8，知P，Q，K三点共线，再注意到性质10证明中的式(4)，可得

图13

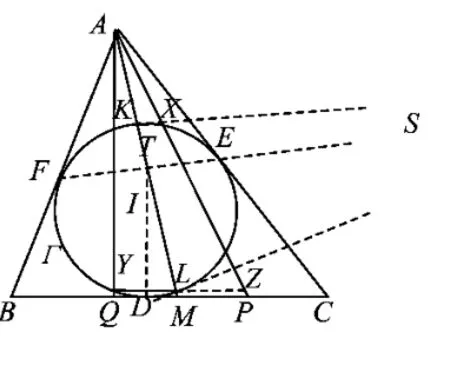
图14

例7已知△ABC的中线AM交其内切圆Γ于点K，L，分别过K，L且平行于BC的直线交圆Γ于点 X，Y，AX，AY 分别交 BC 于点 P，Q．证明:BP=CQ．

(第46届IMO预选题，2006年伊朗国家队选拔赛试题)

证明如图14，设I为△ABC的内心，⊙I分别切边BC，CA，AB 于点 D，E，F，直线 DI与 EF 交于点T．由性质6知，点T在AM上．设过点K，L的2条切线交于点S，则由性质8，知 F，E，S共线．又由性质10，知

设直线YL交AP于点Z，由KX∥YL，得

注意到等腰梯形YLXK中对角线KL及其两底的公垂线为TI，从而

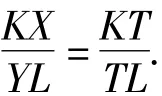
再注意式(8)，式(9)，可得

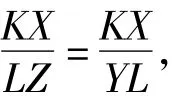
即知L是 YZ的中点，因此 M是QP的中点，故BP=CQ．

［1］ 沈文选．三角形内切圆的几个性质及应用［J］．中学教研(数学)，2011(5):28-32．